数值表示
进制
进制也就是进位制,是人们规定的一种进位方法
对于任何一种进制 X 进制,就表示某一位置上的数运算时是逢 X 进一位
十进制是逢十进一,十六进制是逢十六进一,二进制就是逢二进一,以此类推,x 进制就是逢 x 进位
| 十进制 | 二进制 | 八进制 | 十六进制 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
| 16 | 10000 | 20 | 10 |
二进制
二进制是计算技术中广泛采用的一种数制。二进制数据是用 0 和 1 两个数码来表示的数
- 它的基数为 2,进位规则是“逢二进一”,借位规则是“借一当二”
当前的计算机系统使用的基本上是二进制系统,
数据在计算机中主要是以补码的形式存储的十进制转化二进制的方法:
- 用十进制数除以 2,分别取余数和商数,商数为 0 的时候,将余数倒着数就是转化后的结果

口诀:除二取余,倒序排列法
八进制
八进制,Octal,缩写 OCT 或 O,一种以 8 为基数的计数法,采用 0,1,2,3,4,5,6,7 八个数字,逢八进 1
- 一些编程语言中常常以数字 0 开始表明该数字是八进制
八进制的数和二进制数可以按位对应(八进制一位对应二进制三位),因此常应用在计算机语言中
八进制和二进制互转:

十进制转化八进制的方法:
- 用十进制数除以 8,分别取余数和商数,商数为 0 的时候,将余数倒着数就是转化后的结果

十六进制
十六进制(英文名称:Hexadecimal),同我们日常生活中的表示法不一样,它由 0-9,A-F 组成,字母不区分大小写
与 10 进制的对应关系是:0-9 对应 0-9,A-F(或 a-f) 对应 10-15
十六进制的数和二进制数可以按位对应(十六进制一位对应二进制四位),因此常应用在计算机语言中
十六进制和二进制互转:

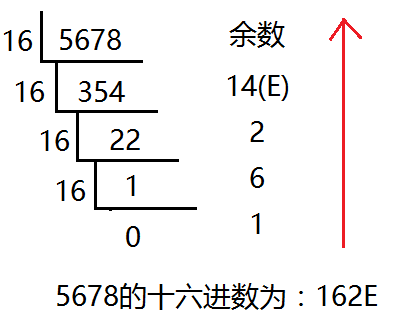
十进制转化十六进制的方法:
用十进制数除以 16,分别取余数和商数,商数为 0 的时候,将余数倒着数就是转化后的结果
C 语言如何表示相应进制数
| 十进制 | 以正常数字 1-9 开头,如 15 |
|---|---|
| 八进制 | 以数字 0 开头,如 017 |
| 十六进制 | 以 0x 或 0X 开头,如 0xf |
| 二进制 | 以 0b 或 0B 开头,如 0b1111 |
示例代码:
#include <stdio.h>
int main() {
// 十进制方式赋值
int a = 15;
// 八进制方式赋值
int b = 017;
// 十六进制方式赋值
int c = 0xf;
// 二进制方式赋值
int d = 0b1111;
printf("%d, %d, %d, %d\n", a, b, c, d);
return 0;
}一个字节二进制转其他进制:
| 7 | 6 | 5 | 4 | - | 3 | 2 | 1 | 0 | 范围 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | - | 1 | 1 | 1 | 1 | 二进制 | 0b0000 0000~ 0b1111 1111 |
| 128 | 64 | 32 | 16 | - | 8 | 4 | 2 | 1 | 十进制 | 0 ~ 255 |
| 0x80 | 0x40 | 0x20 | 0x10 | - | 0x08 | 0x04 | 0x02 | 0x01 | 十六进制 | 0x00 ~ 0xFF |
数值存储方式
计算机底层都是存储数据都是采用二进制,但二进制也有几种,比如:原码、反码、补码。接下来我们来看看他们之间的关系的意义作用。
- 计算机底层存储的二进制都是:补码!
- 正数的原、反、补码都一样
- 负数的原、反、补码不同
原码
十进制数按照:除二取余、倒序排列,得到的就是原码。
- 10 -> 0000 1010
- -10 -> 1000 1010
- -1 -> 1000 0001
- 1 -> 0000 0001
问题: 原码在做计算的时候会出现一些问题,比如正负数的加法运算,以及零的问题。
正负数加法
- -1 + 1 = 0
1000 0001 + 0000 0001 ---------------- 1000 0010 -> -2 ?正负零
- +0 和 -0
- 十进制数字 0,占了两个二进制;
0000 0000 1000 0000
反码
为了解决上面的问题,出现了反码,反码的计算规则如下:
- 正数的反码就是原码本身;
- 负数的反码是按位取反(但符号位不变);
示例
- 1 -> 0000 0001(二进制) -> 0000 0001(反码)
- -1 -> 1000 0001(二进制) -> 1111 1110(反码)
0000 0001
+ 1111 1110
-----------------
1111 11111111 1111 是运算完之后的结果,但要注意,这时还是反码,需要重新返回来:1000 0000。
反码解决了正负数加法问题,但正负零的问题还是存在。
补码
正数的补码就是原码本身;
负数的补码就是在反码的基础上 +1;
- 1 -> 0000 0001(二进制) -> 0000 0001(反码) -> 0000 0001(补码)
- -1 -> 1000 0001(二进制) -> 1111 1110(反码) -> 1111 1111(补码)
0000 0001
+ 1111 1111
----------------
0000 0000补码在正负数加减法运算时没问题,也不会出现正负零占两个二进制。但 1000 0000 不表示为负零,用来表示什么呢?计算机其实默认把 8 位有符号二进制 1000 0000 表示为 -128。
int8_t e = 0b10000000;
printf("%d\n", e);数值范围
一个字节(8bit),能表示的数据范围(用原码表示):
- uint8_t 无符号数: (0 ~ 255) 0000 0000 ~ 1111 1111
- int8_t 有符号数: (-127 ~ 0 ~ 127) 1111 1111 ~ 0000 0000 ~ 0111 1111
- int8_t 有符号数:(-128)1000 0000