机器学习前置基础

矩阵和向量

矩阵（知道）

矩阵，英文 matrix，和 array 的区别矩阵必须是 2 维的，但是 array 可以是多维的。

如图：这个是 $3\times 2$ 矩阵，即 3 行 2 列，如 $m$ 为行，$n$ 为列，那么 $m\times n$ 即 $3\times 2$

$$\left[\begin{array}{cc}1& 2\\ 3& 4\\ 5& 6\end{array}\right]$$

矩阵的维数即 行数×列数

矩阵元素 (矩阵项):

$$A=\left[\begin{array}{cc}1& 2\\ 3& 4\\ 5& 6\end{array}\right]$$

$A_{(}ij)$ 指第 $i$ 行，第 $j$ 列的元素。

向量

向量是一种特殊的矩阵，讲义中的向量一般都是列向量，下面展示的就是三维列 向量 (3×1)。

$$A=\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right]$$

运算

加法和标量乘法

矩阵的加法：行列数相等的可以加。

例：

$$\left[\begin{array}{cc}1& 2\\ 3& 4\\ 5& 6\end{array}\right]+\left[\begin{array}{cc}1& 2\\ 3& 4\\ 5& 6\end{array}\right]=\left[\begin{array}{cc}2& 4\\ 6& 8\\ 10& 12\end{array}\right]$$

矩阵的乘法：每个元素都要乘。

例:3

$$3\ast \left[\begin{array}{cc}1& 2\\ 3& 4\\ 5& 6\end{array}\right]=\left[\begin{array}{cc}3& 6\\ 9& 12\\ 15& 18\end{array}\right]$$

组合算法也类似。

矩阵向量乘法

矩阵和向量的乘法如图：m×n 的矩阵乘以 n×1 的向量，得到的是 m×1 的向量

例：

$$\left[\begin{array}{cc}1& 3\\ 4& 0\\ 2& 1\end{array}\right]\ast \left[\begin{array}{c}1\\ 5\end{array}\right]=\left[\begin{array}{c}16\\ 4\\ 7\end{array}\right]$$

1*1+3*5 = 16
4*1+0*5 = 4
2*1+1*5 = 7

矩阵乘法遵循准则：

(M 行，N 列)*(N 行，L 列) = (M 行，L 列)

矩阵乘法

矩阵乘法：

m×n 矩阵乘以 n×o 矩阵，变成 m×o 矩阵。

举例：比如说现在有两个矩阵 A 和 B，那 么它们的乘积就可以表示为图中所示的形式。

练一练

$$A=\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 0\end{array}\right]B=\left[\begin{array}{ccc}1& 2& 1\\ 1& 1& 2\\ 2& 1& 1\end{array}\right]$$

求矩阵 AB 的结果

答案：

$$B=\left[\begin{array}{ccc}1\ast 1+2\ast 1+3\ast 2& 1\ast 2+2\ast 1+3\ast 1& 1\ast 1+2\ast 2+3\ast 1\\ 4\ast 1+5\ast 1+6\ast 2& 4\ast 2+5\ast 1+6\ast 1& 4\ast 1+5\ast 2+6\ast 1\\ 7\ast 1+8\ast 1+0\ast 2& 7\ast 2+8\ast 1+0\ast 1& 7\ast 1+8\ast 2+0\ast 1\end{array}\right]=\left[\begin{array}{ccc}9& 7& 8\\ 21& 19& 20\\ 15& 22& 23\end{array}\right]$$

矩阵乘法的性质

矩阵的乘法不满足交换律：A×B≠B×A

矩阵的乘法满足结合律。即：A×（B×C）=（A×B）×C

单位矩阵：在矩阵的乘法中，有一种矩阵起着特殊的作用，如同数的乘法中的 1，我们称 这种矩阵为 单位矩阵．它是个方阵，一般用 I 或者 E 表示，从 左上角到右下角的对角线（称为主对角线）上的元素均为 1 以外全都为 0。如：

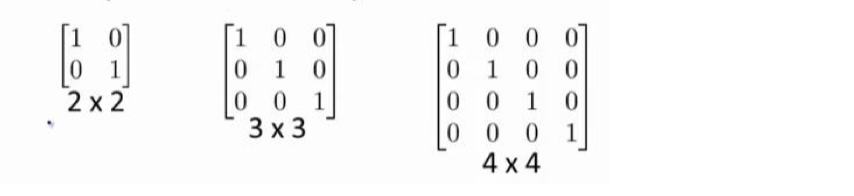
逆、转置

矩阵的逆：如矩阵 A 是一个 m×m 矩阵（方阵），如果有逆矩阵，则：

$$A{A}^{-1}=A^{-1}A=1$$

低阶矩阵求逆的方法：

1. 待定系数法

2. 初等变换

矩阵的转置：设 A 为 m×n 阶矩阵（即 m 行 n 列），第 i 行 j 列的元素是 $a(i,j)$，即：

$A=a(i,j)$

定义 A 的转置为这样一个 n×m 阶矩阵 B，满足 $B=a(j,i)$，即 $b(i,j)=a(j,i)$（B 的第 i 行第 j 列元素是 A 的第 j 行第 i 列元素），记 $AT=B$。

直观来看，将 A 的所有元素绕着一条从第 1 行第 1 列元素出发的右下方 45 度的射线作 镜面反转，即得到 A 的转置。

例：

$${\left[\begin{array}{cc}a& b\\ c& d\\ e& f\end{array}\right]}^T=\left[\begin{array}{ccc}a& c& e\\ b& d& f\end{array}\right]$$

矩阵运算 API

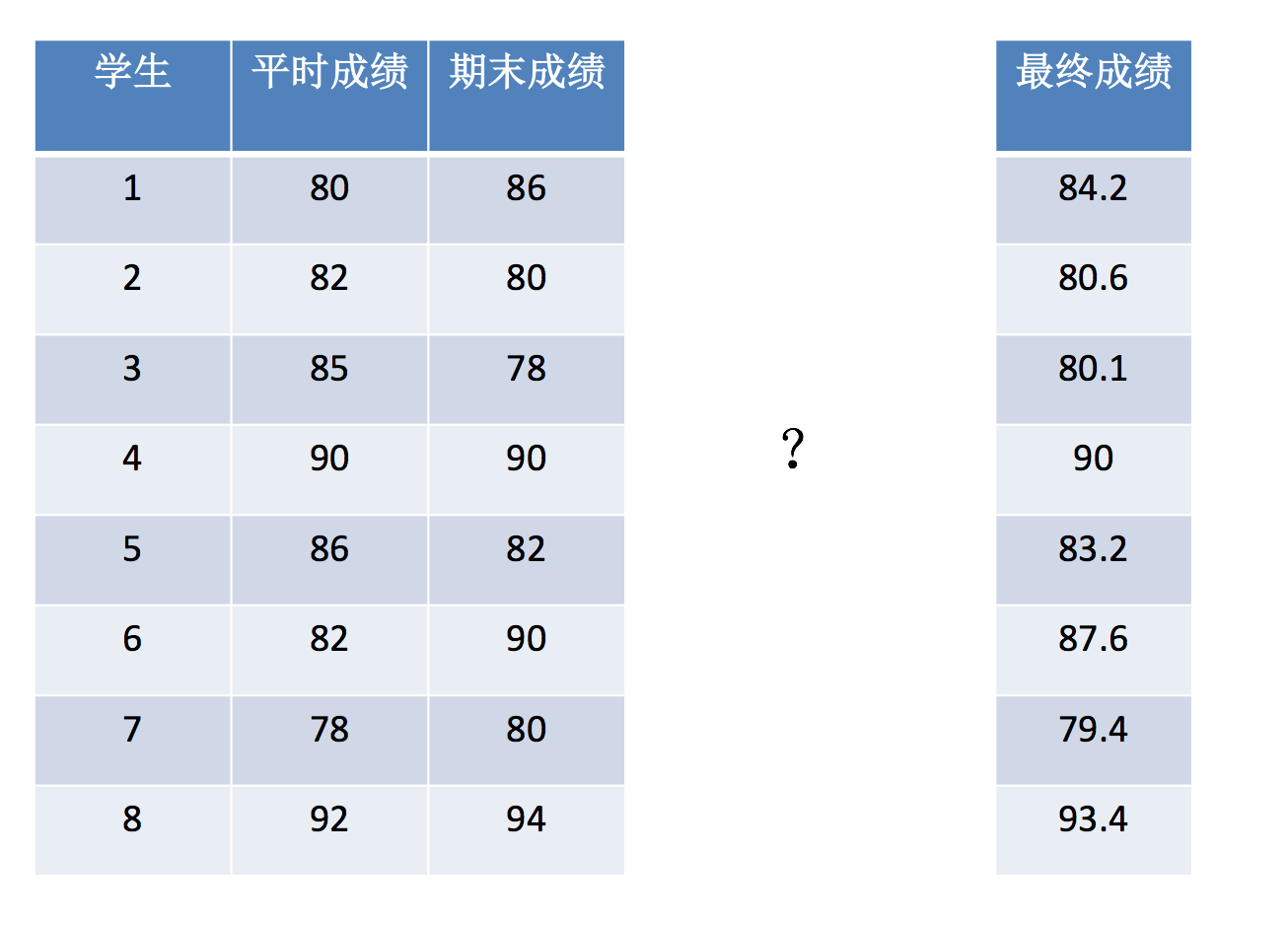
矩阵乘法

• np.matmul
• np.dot

a = np.array([
    [80, 86],
    [82, 80],
    [85, 78],
    [90, 90],
    [86, 82],
    [82, 90],
    [78, 80],
    [92, 94]]
)
b = np.array([[0.7], [0.3]])

np.matmul(a, b)

np.dot(a, b)

np.matmul 和 np.dot 的区别：

二者都是矩阵乘法。 np.matmul 中禁止矩阵与标量的乘法。在矢量乘矢量的內积运算中，np.matmul 与 np.dot 没有区别。

"""作用不同的情况"""
a = np.array([
    [
        [0, 1, 2],
        [3, 4, 5]],
    [
        [6, 7, 8],
        [9, 10, 11]
    ]
])

b = np.array([
    [
        [0, 1],
        [2, 3],
        [4, 5]],

    [
        [6, 7],
        [8, 9],
        [10, 11]
    ]
])

print('np.matmul(a,b):\n', np.matmul(a, b))
print('np.dot(a,b):\n', np.dot(a, b))

"""
np.matmul(a,b):
 [[[ 10  13]
  [ 28  40]]

 [[172 193]
  [244 274]]]
np.dot(a,b):
 [[[[ 10  13]
   [ 28  31]]

  [[ 28  40]
   [100 112]]]


 [[[ 46  67]
   [172 193]]

  [[ 64  94]
   [244 274]]]]
"""

matmul 将最后两维作为矩阵的两维，相当于有 2 个 2 ∗ 2 的矩阵，因此通过对应位置矩阵进行矩阵乘法，会得到 2 个 2 ∗ 2 的结果

可以看到其结果与 matmul 不同并且结果是四维的，这是因为 dot 将 a 数组的最后一维作为向量，并将 b 数组的倒数第二维作为了另一个向量，因此 a 中可以看成有 2 ∗ 2 个向量，b 中有 2 ∗ 2 个向量，dot 会将 a 的向量与 b 的向量全部组合在一起，因此会有 ( 2 ∗ 2 ) ∗ ( 2 ∗ 2 ) 种结果。

距离度量

欧式距离 (Euclidean Distance)

欧氏距离是最容易直观理解的距离度量方法，我们小学、初中和高中接触到的两个点在空间中的距离一般都是指欧氏距离。

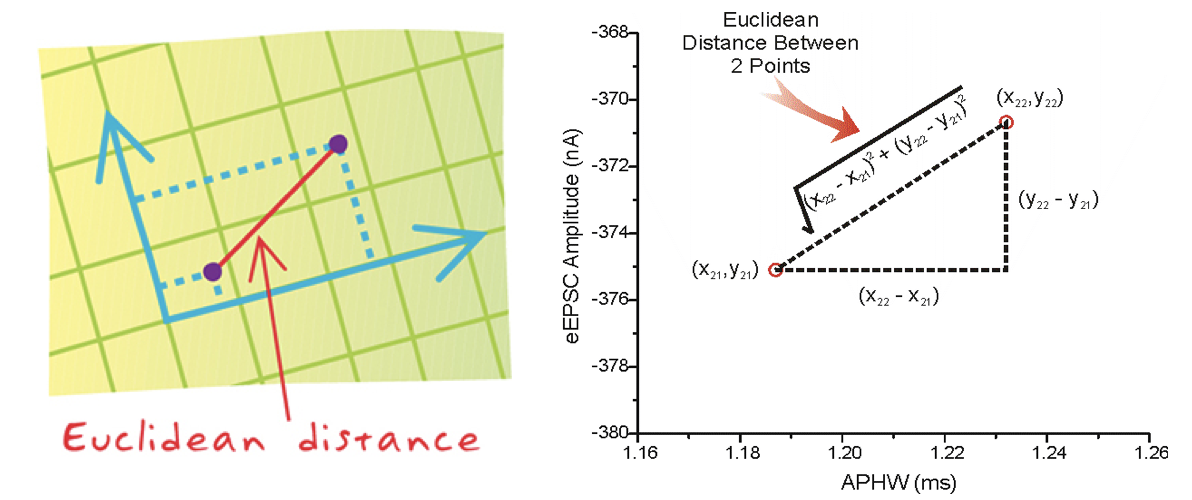
二维平面上的点 $a(x_1,y_1)$ 与 $b(x_2,y_2)$ 间的欧氏距离：

$$d_{12}=\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2}$$

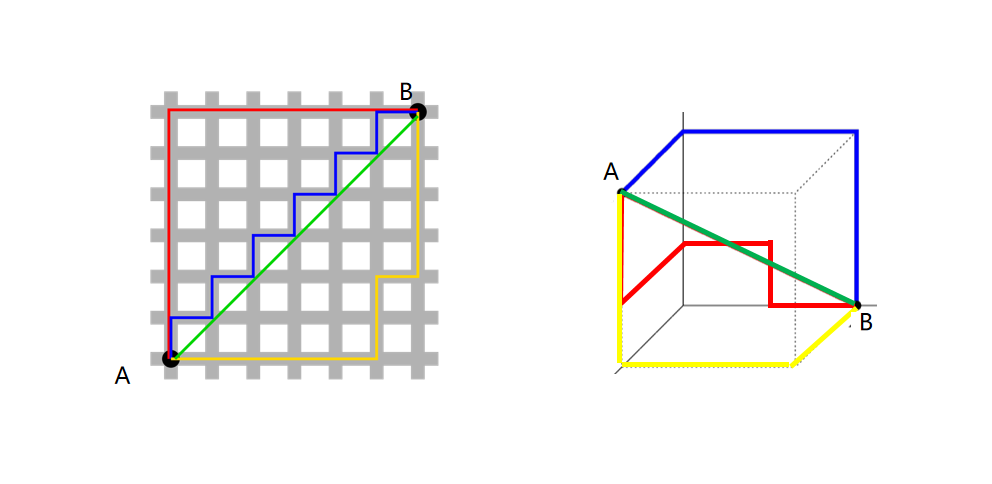
三维空间点 $a(x_1,y_1,z_1)$ 与 $b(x_2,y_2,z_2)$ 间的欧氏距离：

$$d_{12}=\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2+(z_1-z_2{)}^2}$$

n 维控件点 $a(x_{11},x_{12},\cdots ,x_{1n})$ 与 $b(x_{21},x_{22},\cdots ,x_{2n})$ 间的欧氏距离（两个 n 维向量）：

$$d_{12}=\sqrt{\sum _{i=1}^n(x_{1k}-x_{2k}{)}^2}$$

举例：

X=[[1,1],[2,2],[3,3],[4,4]];
经计算得:
d = 1.4142    2.8284     4.2426    1.4142    2.8284    1.4142

曼哈顿距离 (Manhattan Distance)

在曼哈顿街区要从一个十字路口开车到另一个十字路口，驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是“曼哈顿距离”。 曼哈顿距离也称为“城市街区距离”(City Block distance)。

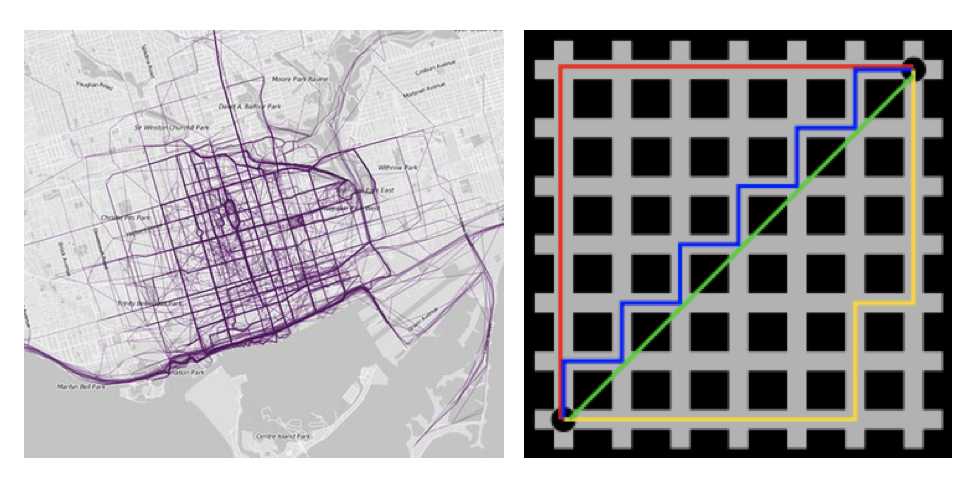
二维平面两点$a(x_1,y_1)$与$b(x_2,y_2)$间的曼哈顿距离 :

$$d_{12}=|x_1-x_2|+|y_1-y_2|$$

n 维空间点$a(x_{11},x_{12},...,x_{1n})$ 与 $b(x_{21},x_{22},...,x_{2n})$ 的曼哈顿距离：

$$d_{12}=\sum _{k=1}^n|x_{1k}-x_{2k}|$$

举例：

X=[[1,1],[2,2],[3,3],[4,4]];
经计算得:
d =   2     4     6     2     4     2

切比雪夫距离 (Chebyshev Distance)

国际象棋中，国王可以直行、横行、斜行，所以国王走一步可以移动到相邻 8 个方格中的任意一个。国王从格子 (x1,y1) 走到格子 (x2,y2) 最少需要多少步？这个距离就叫切比雪夫距离。

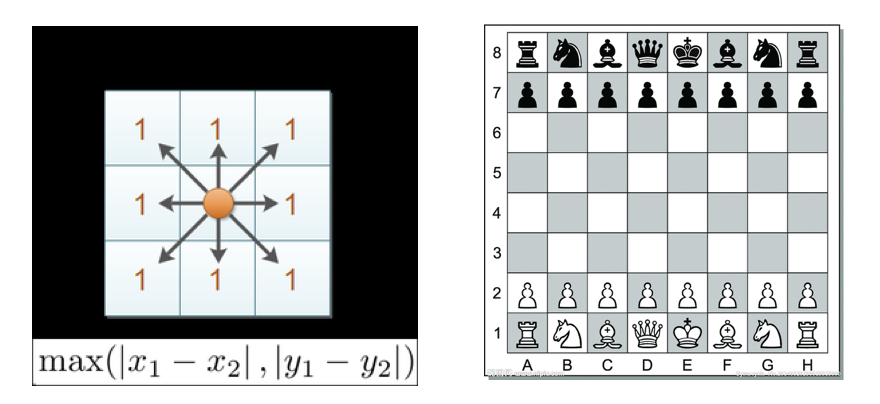
二维平面两点$a(x_1,y_1)$与$b(x_2,y_2)$间的切比雪夫距离 :

$$d_{12}=max(|x_1-x_2|,|y_1-y_2|)$$

n 维空间点$a(x_{11},x_{12},...,x_{1n})$ 与 $b(x_{21},x_{22},...,x_{2n})$ 的曼哈顿距离：

$$d_{12}=max(|x_{1i}-x_{2i}|)$$

举例：

X=[[1,1],[2,2],[3,3],[4,4]];
经计算得:
d =   1     2     3     1     2     1

闵可夫斯基距离 (Minkowski Distance)

闵氏距离不是一种距离，而是一组距离的定义，是对多个距离度量公式的概括性的表述。

n 维空间点$a(x_{11},x_{12},...,x_{1n})$ 与 $b(x_{21},x_{22},...,x_{2n})$ 的闵可夫斯基距离：

$$\begin{gathered} d_{12}=\sqrt[p]{ \\ \sum _{k=1}^n|x_{1k}-x_{2k}{|}^p} \end{gathered}$$

其中 p 是一个变参数：

当 p=1 时，就是曼哈顿距离；

当 p=2 时，就是欧氏距离；

当 p→∞时，就是切比雪夫距离。

根据 p 的不同，闵氏距离可以表示某一类/种的距离。

小结：

1 闵氏距离，包括曼哈顿距离、欧氏距离和切比雪夫距离都存在明显的缺点：

e.g. 二维样本 (身高[单位:cm],体重[单位:kg])，现有三个样本：a(180,50)，b(190,50)，c(180,60)。

a 与 b 的闵氏距离（无论是曼哈顿距离、欧氏距离或切比雪夫距离）等于 a 与 c 的闵氏距离。但实际上身高的 10cm 并不能和体重的 10kg 划等号。

2 闵氏距离的缺点：

(1) 将各个分量的量纲 (scale)，也就是“单位”相同的看待了;

(2) 未考虑各个分量的分布（期望，方差等）可能是不同的。

标准化欧氏距离 (Standardized EuclideanDistance)

标准化欧氏距离是针对欧氏距离的缺点而作的一种改进。

思路：既然数据各维分量的分布不一样，那先将各个分量都“标准化”到均值、方差相等。

Sk(下标) 表示各个维度的标准差

标准化欧氏距离公式：

$$\begin{gathered} d_{12}=\sqrt[p]{ \\ \sum _{k=1}^n( \\ \frac{x_{1k}-x_{2k}}{s_k}{)}^2} \end{gathered}$$

如果将方差的倒数看成一个权重，也可称之为加权欧氏距离 (Weighted Euclidean distance)。

举例：

X=[[1,1],[2,2],[3,3],[4,4]];（假设两个分量的标准差分别为 0.5 和 1）
经计算得:
d =   2.2361    4.4721    6.7082    2.2361    4.4721    2.2361

余弦距离 (Cosine Distance)

几何中，夹角余弦可用来衡量两个向量方向的差异；机器学习中，借用这一概念来衡量样本向量之间的差异。

• 二维空间中向量 A(x1,y1) 与向量 B(x2,y2) 的夹角余弦公式：

  

• 两个 n 维样本点 a(x11,x12,…,x1n) 和 b(x21,x22,…,x2n) 的夹角余弦为：

  

• 即：

  

夹角余弦取值范围为[-1,1]。余弦越大表示两个向量的夹角越小，余弦越小表示两向量的夹角越大。当两个向量的方向重合时余弦取最大值 1，当两个向量的方向完全相反余弦取最小值 -1。

举例：

X=[[1,1],[1,2],[2,5],[1,-4]]
经计算得:
d =   0.9487    0.9191   -0.5145    0.9965   -0.7593   -0.8107

汉明距离 (Hamming Distance)【了解】

两个等长字符串 s1 与 s2 的汉明距离为：将其中一个变为另外一个所需要作的最小字符替换次数。

例如：

  The Hamming distance between "1011101" and "1001001" is 2.
  The Hamming distance between "2143896" and "2233796" is 3.
  The Hamming distance between "toned" and "roses" is 3.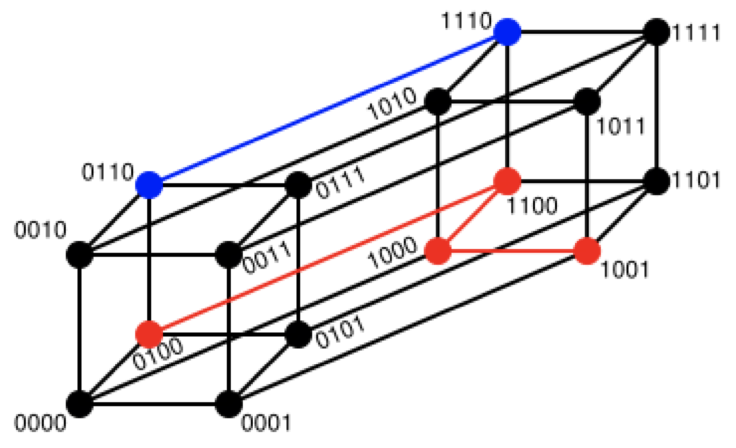

随堂练习：
求下列字符串的汉明距离：

  1011101 与 1001001 　

  2143896 与 2233796
　
  irie 与 rise

汉明重量：是字符串相对于同样长度的零字符串的汉明距离，也就是说，它是字符串中非零的元素个数：对于二进制字符串来说，就是 1 的个数，所以 11101 的汉明重量是 4。因此，如果向量空间中的元素 a 和 b 之间的汉明距离等于它们汉明重量的差 a-b。

应用：汉明重量分析在包括信息论、编码理论、密码学等领域都有应用。比如在信息编码过程中，为了增强容错性，应使得编码间的最小汉明距离尽可能大。但是，如果要比较两个不同长度的字符串，不仅要进行替换，而且要进行插入与删除的运算，在这种场合下，通常使用更加复杂的编辑距离等算法。

举例：

X=[[0,1,1],[1,1,2],[1,5,2]]
注：以下计算方式中，把 2 个向量之间的汉明距离定义为 2 个向量不同的分量所占的百分比。

经计算得:
d =   0.6667    1.0000    0.3333

杰卡德距离 (Jaccard Distance)【了解】

杰卡德相似系数 (Jaccard similarity coefficient) ：两个集合 A 和 B 的交集元素在 A，B 的并集中所占的比例，称为两个集合的杰卡德相似系数，用符号 J(A,B) 表示：

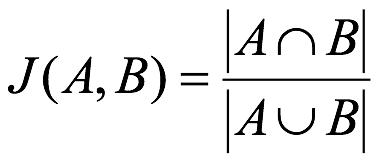
杰卡德距离 (Jaccard Distance)：与杰卡德相似系数相反，用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度：

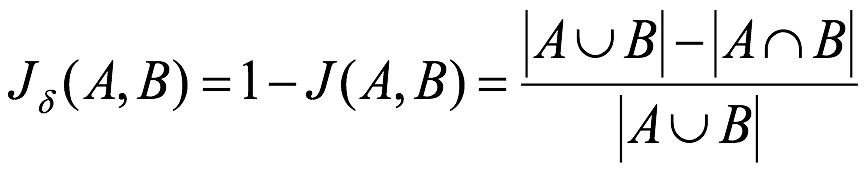
举例：

X=[[1,1,0][1,-1,0],[-1,1,0]]
注：以下计算中，把杰卡德距离定义为不同的维度的个数占“非全零维度”的比例
经计算得:
d =   0.5000    0.5000    1.0000

马氏距离 (Mahalanobis Distance)【了解】

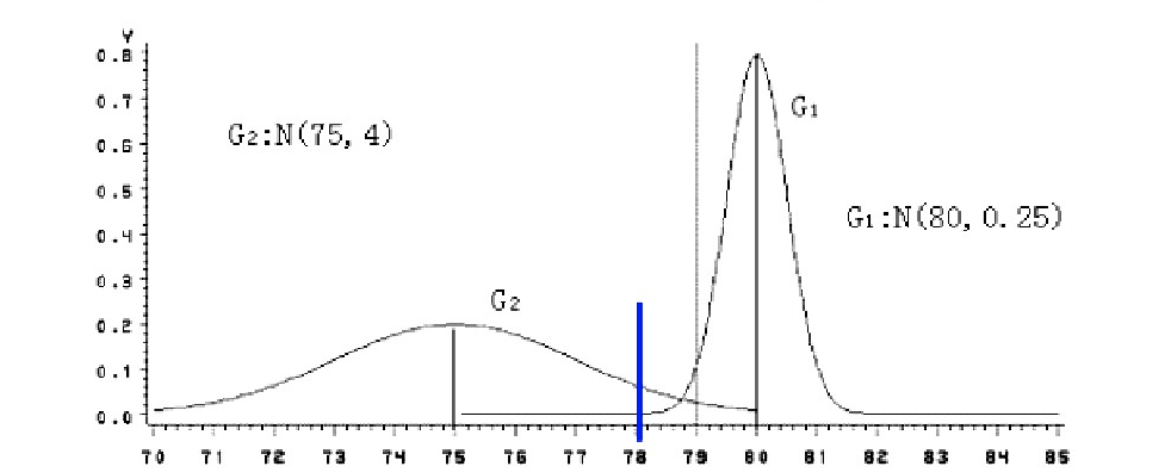
下图有两个正态分布图，它们的均值分别为 a 和 b，但方差不一样，则图中的 A 点离哪个总体更近？或者说 A 有更大的概率属于谁？显然，A 离左边的更近，A 属于左边总体的概率更大，尽管 A 与 a 的欧式距离远一些。这就是马氏距离的直观解释。

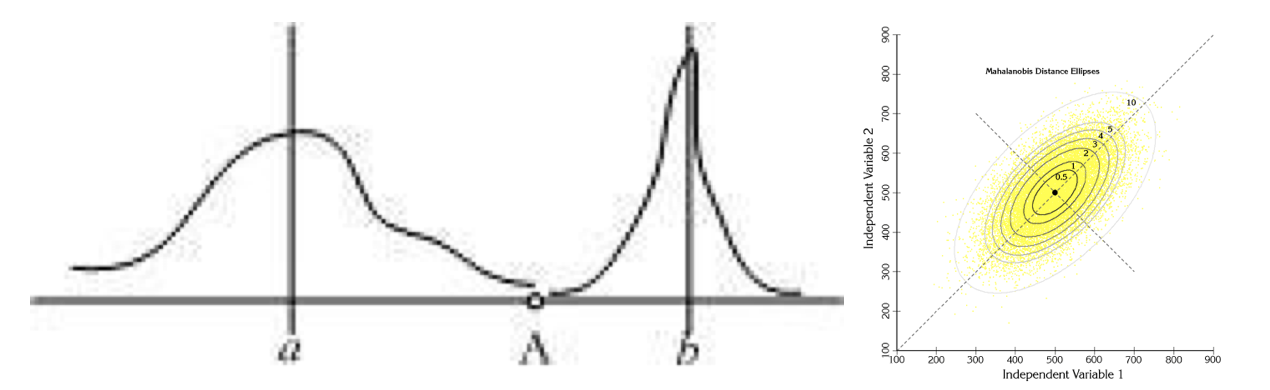
马氏距离是基于样本分布的一种距离。

马氏距离是由印度统计学家马哈拉诺比斯提出的，表示数据的协方差距离。它是一种有效的计算两个位置样本集的相似度的方法。

与欧式距离不同的是，它考虑到各种特性之间的联系，即独立于测量尺度。

**马氏距离定义：**设总体 G 为 m 维总体（考察 m 个指标），均值向量为μ=（μ1，μ2，… ...，μm，）`,协方差阵为∑=（σij）,

则样本 X=（X1，X2，… …，Xm，）`与总体 G 的马氏距离定义为：

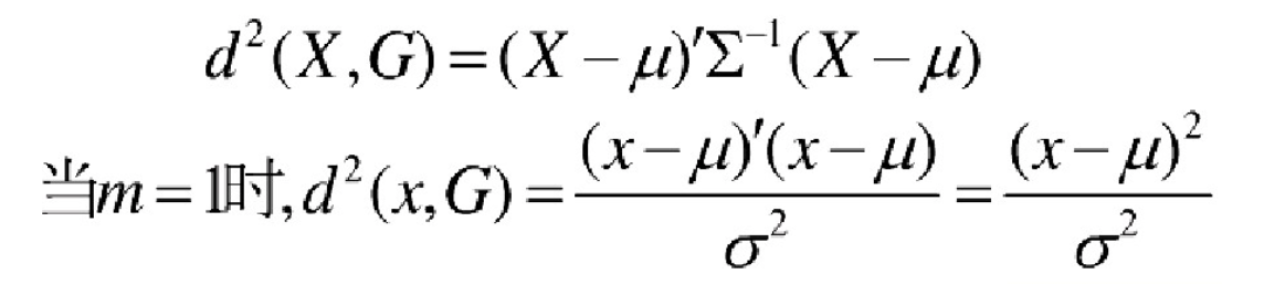
马氏距离也可以定义为两个服从同一分布并且其协方差矩阵为∑的随机变量的差异程度：如果协方差矩阵为单位矩阵，马氏距离就简化为欧式距离；如果协方差矩阵为对角矩阵，则其也可称为正规化的欧式距离。

马氏距离特性：

1. 量纲无关，排除变量之间的相关性的干扰；

2. 马氏距离的计算是建立在总体样本的基础上的，如果拿同样的两个样本，放入两个不同的总体中，最后计算得出的两个样本间的马氏距离通常是不相同的，除非这两个总体的协方差矩阵碰巧相同；

3. 计算马氏距离过程中，要求总体样本数大于样本的维数，否则得到的总体样本协方差矩阵逆矩阵不存在，这种情况下，用欧式距离计算即可。

4. 还有一种情况，满足了条件总体样本数大于样本的维数，但是协方差矩阵的逆矩阵仍然不存在，比如三个样本点（3，4），（5，6），（7，8），这种情况是因为这三个样本在其所处的二维空间平面内共线。这种情况下，也采用欧式距离计算。

欧式距离&马氏距离：

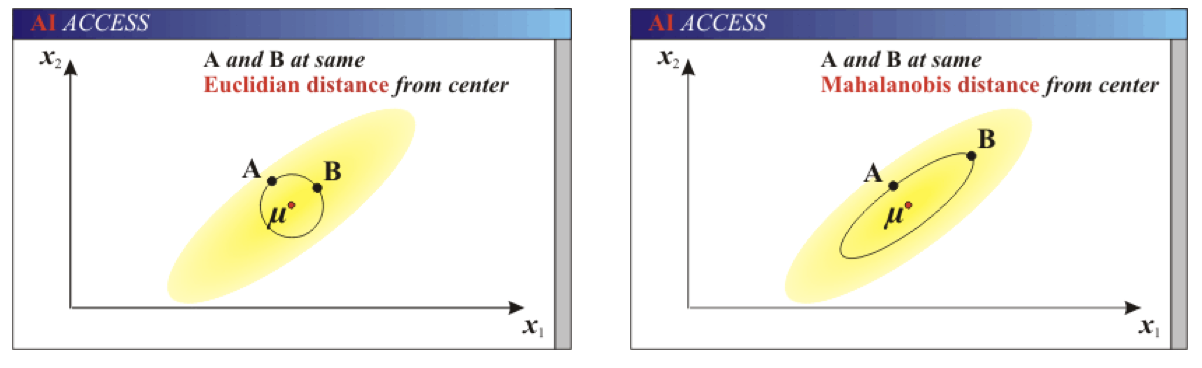
举例：

已知有两个类 G1 和 G2，比如 G1 是设备 A 生产的产品，G2 是设备 B 生产的同类产品。设备 A 的产品质量高（如考察指标为耐磨度 X），其平均耐磨度 $\mu 1=80$，反映设备精度的方差 $\sigma 2(1)=0.25$; 设备 B 的产品质量稍差，其平均耐磨损度 $\mu 2=75$，反映设备精度的方差 $\sigma 2(2)=4$.

今有一产品 G0，测的耐磨损度 $X_0=78$，试判断该产品是哪一台设备生产的？

直观地看，$X_0$ 与 $\mu 1$（设备 A）的绝对距离近些，按距离最近的原则，是否应把该产品判断设备 A 生产的？

考虑一种相对于分散性的距离，记 $X_0$ 与 $G_1$，$G_2$ 的相对距离为 $d_1$，$d_2$,则：

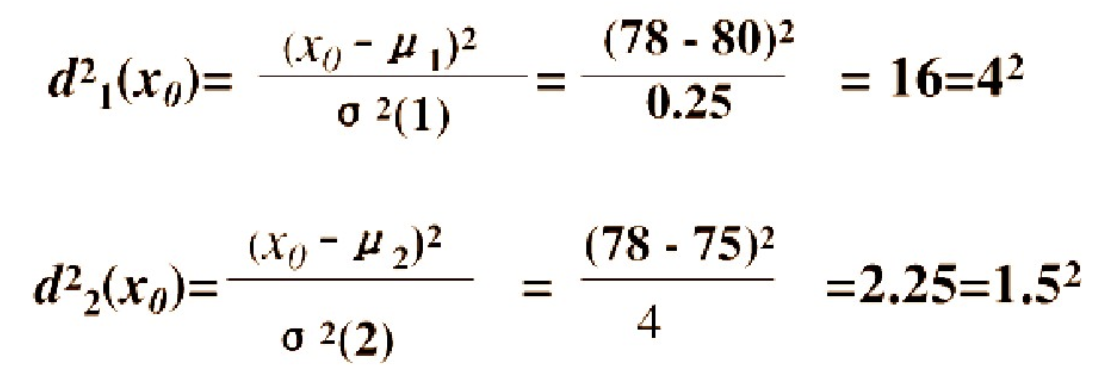
因为 $d_2=1.5<d_1=4$，按这种距离准则，应判断 $X_0$ 为设备 B 生产的。

设备 B 生产的产品质量较分散，出现 $X_0$ 为 78 的可能性较大；而设备 A 生产的产品质量较集中，出现 $X_0$ 为 78 的可能性较小。

这种相对于分散性的距离判断就是马氏距离。

数学：求导

常见函数的导数

导数的四则运算

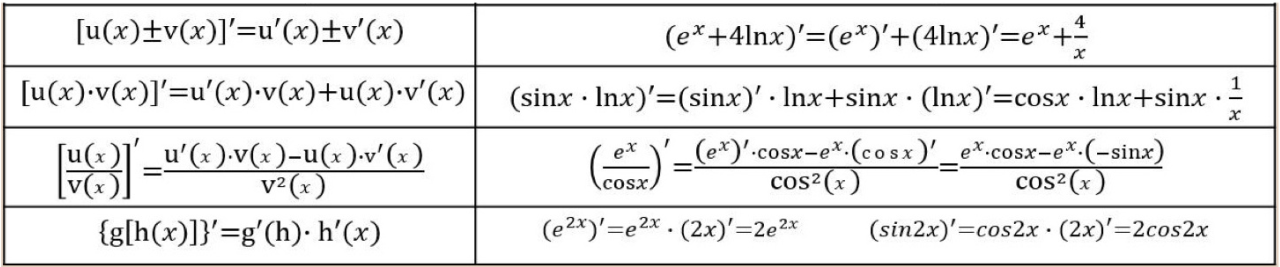
矩阵（向量）求导 [了解]

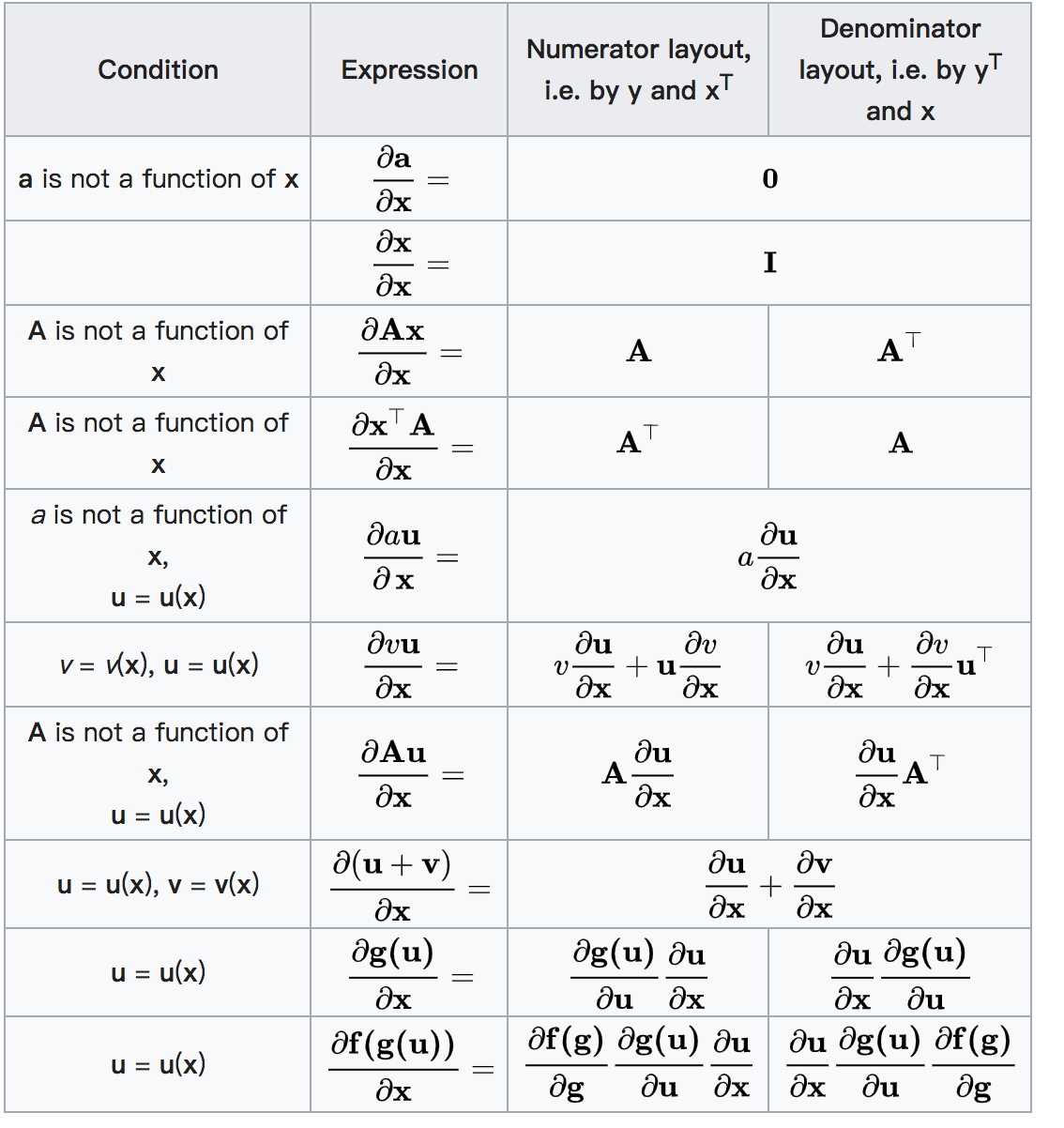
参考链接：https://en.wikipedia.org/wiki/Matrix_calculus#Scalar-by-vector_identities