k-均值算法
k-均值算法是一种典型的无监督机器学习算法,用来解决聚类问题 (Clustering) 。这也是一个无监督的学习算法。但这并不意味着无监督机器学习不重要。相反,由于数据标记需要耗费巨大的资源,无监督或者半监督的学习算法近来逐渐受到学者青睐,原因是不需要对数据进行标记,可以大大减少工作量。本章涵盖的内容如下:
k-均值算法的成本函数;
k-均值算法的原理及计算步骤;
通过一个简单的实例,介绍 scikit-learn 里的 k-均值算法;
使用 k-均值算法进行文本分类;
聚类问题的性能评估方法。
算法原理
聚类问题和分类问题的区别。针对监督式学习算法,如 k-近邻算法,其输入数据是已经标记了的
k-均值算法算法包含以下两个步骤。
(1) 给聚类中心分配点。计算所有的训练样例,把每个训练样例分配到距离其最近的聚类中心所在的类别里。
(2) 移动聚类中心。新的聚类中心移动到这个聚类所有的点的平均值处。
一直重复做上面的动作,直到聚类中心不再移动为止,这时就探索出了数据集的结构了。
我们也可以用数学方法来描述 k-均值算法。算法有两个输入信息,一是 k,表示选取的聚类个数;另一个是训练数据集
(1) 随机选择 k 个聚类中心
(2) 从 1~m 中遍历所有的数据集,计算
(3) 从 1~k 中遍历所有的聚类中心,移动聚类中心的新位置到这个聚类的均值处。即
其中
(4) 重复步骤 (2),直到聚类中心不再移动为止。
牧师 - 村民模型 K-means 有一个著名的解释:牧师—村民模型:
有四个牧师去郊区布道,一开始牧师们随意选了几个布道点,并且把这几个布道点的情况公告给了郊区所有的村民,于是每个村民到离自己家最近的布道点去听课。 听课之后,大家觉得距离太远了,于是每个牧师统计了一下自己的课上所有的村民的地址,搬到了所有地址的中心地带,并且在海报上更新了自己的布道点的位置。 牧师每一次移动不可能离所有人都更近,有的人发现 A 牧师移动以后自己还不如去 B 牧师处听课更近,于是每个村民又去了离自己最近的布道点…… 就这样,牧师每个礼拜更新自己的位置,村民根据自己的情况选择布道点,最终稳定了下来。 我们可以看到该牧师的目的是为了让每个村民到其最近中心点的距离和最小。
k-均值算法成本函数
根据成本函数的定义,成本即模型预测值与实际值的误差,据此不难得出 k-均值算法的成本函数:
其中,
随机初始化聚类中心点
假设 k 是聚类的个数,m 是训练样本的个数,那么必定有 k<m。在随机初始化时,随机从 m 个训练数据集里选择 k 个样本作为聚类中心点。这是正式推荐的随机初始化聚类中心的做法。
在实际解决问题时,最终的聚类结果会和随机初始化的聚类中心点有关。即不同的随机初始化的聚类中心点可能得到不同的最终聚类结果。因为成本函数可能会收敛在一个局部最优解,而不是全局最优解上。有一个解决方法就是多做几次随机初始化的动作,然后训练出不同的聚类中心点及聚类节点分配方案,然后用这些值算出成本函数,从中选择成本最小的那个函数。
假设我们做 100 次运算,步骤如下:
(1) 随机选择 k 个聚类中心点。
(2) 运行 k-均值算法,算出 c^(1)^,c^(2)^,…,c^(m)^ 和 u~1~,u~2~,…,u~k~。
(3) 使用 c^(1)^,c^(2)^,…,c^(m)^ 和 u~1~,u~2~,…,u~k~ 算出最终的成本值。
(4) 记录最小的成本值,然后跳回步骤 (1),直到达到最大运算次数。
这样就可以适当加大运算次数,从而求出全局最优解。
选择聚类的个数
怎样选择合适的聚类个数呢?实际上聚类个数和业务有紧密的关联,例如我们要对运动鞋的尺码大小进行聚类分析,那么是分成 5 个尺寸等级好还是分成 10 个尺寸等级好呢?这个是个业务问题而非技术问题。5 个尺寸等级可以给生产和销售带来便利,但客户体验可能不好;10 个尺寸等级客户体验好了,可能会给生产和库存造成不便。
从技术角度来讲,也有一些方法可以用来做一些判断的。我们可以把聚类个数作为横坐标,成本函数作为纵坐标,把成本和聚类个数的数据画出来。大体的趋势是随着 k 值越来越大,成本会越来越低。我们找出一个拐点,即在这个拐点之前成本下降比较快,在这个拐点之后,成本下降比较慢,那么很可能这个拐点所在的 k 值就是要寻求的最优解。
当然,这个技术方法并不总是有效的,因为很可能会得到一个没有拐点的曲线,这样,就必须和业务逻辑结合以便选择合适的聚类个数。
k-均值案例
案例里面已经提前准备好了 80 条二维数据,我们需要做的就是讲这些数据进行聚类。
x1,x2
1.658985,4.285136
-3.453687,3.424321
4.838138,-1.151539
-5.379713,-3.362104
0.972564,2.924086
....可以看到该数据集很简单,只有两列,存储格式是 csv 格式,整个数据集共有 80 个样本。肉眼观察就能知道没有缺失值。
查看数据分布如下
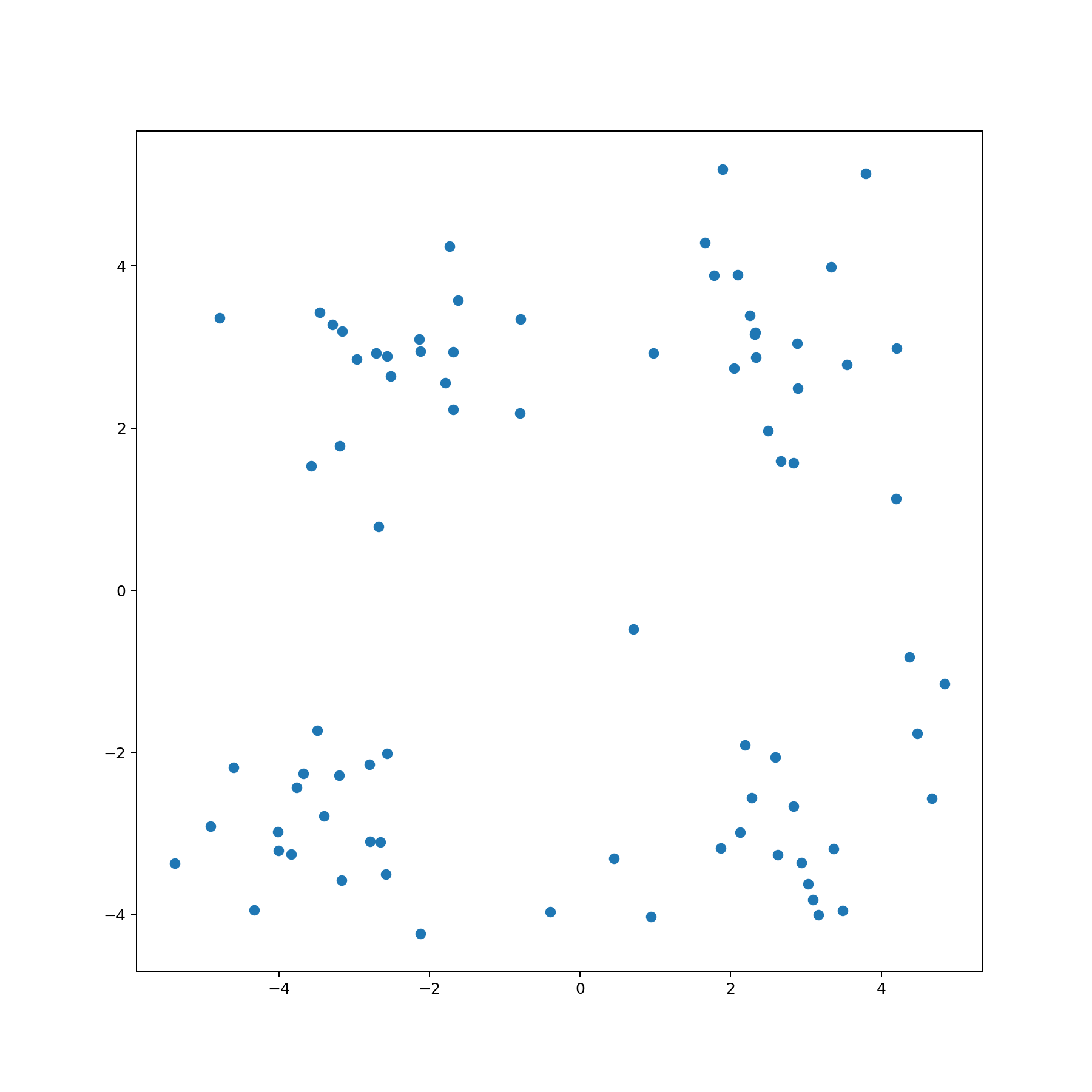
数据集很明显的分为 4 类,这也是观察容易看出来的,所以在后期分类的话就要分成 4 类。这是对于这个简单数据集来说的,若真实业务中可能会根据业务需求来分类。
1、K-Means 算法原理
1.1、欧氏距离
K-Means 算法的核心就是欧氏距离,通过欧氏距离可以在多维空间中计算出点的相近程度从而把最近的点归为一类。其具体公式为:
即 X 点和 Y 点的距离就是 X、Y 各维数据之差平方求和,最后取根号。
1.2、聚类步骤
K-Means 算法存在一个质心的概念,就是该簇的中心点,而在算法开始的时候质心是随机生成的。下面通过流程图来解释算法:
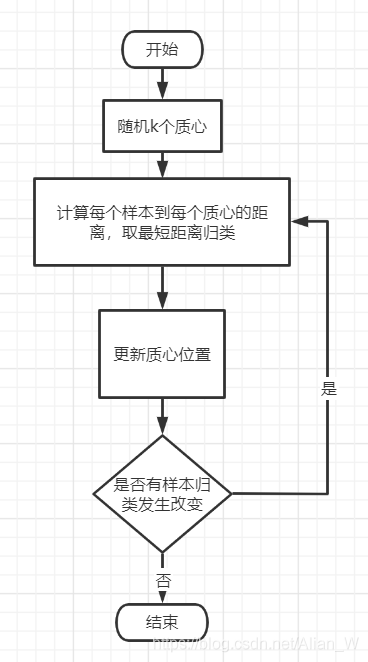
可以看到流程图还是很简单的,这就是 K-Means 的最基本的思想:随机质心->更新样本类别->根据簇中样本更新质心->直到没有新的样本改变簇类别。
2、设计算法
在 1.2 中我们已经知道程序的流程图,但是还存在几个关键的步骤没有解决,在这里逐一列举出来:
1、随机质心怎么做
2、样本到质心距离怎么计算
3、什么时候更新质心位置
4、如何判断样本归类有变化
2.1 如何随机质心
随机质心必须让质心保持在数据集的范围内,即每一维数据的最大最小值之内。同时根据分类数目(k)来构造质心数目。
def create_centers(data_matrix, k=4):
# 先把数计算出来降低时间复杂度
n, m = np.shape(data_matrix)
# 根据数据集创建随机质心 shape=[k,m] 保存质心的坐标
center_matrix = np.zeros(shape=(k, m))
for i in range(m):
min_val, max_val = min(data_matrix[:, i])[0, 0], max(data_matrix[:, i])[0, 0]
center_matrix[:, i] = np.array((min_val + (max_val - min_val) * np.random.rand(k, 1)))[:, 0]
center_matrix = np.mat(center_matrix)
return center_matrix2.2 样本到质心距离计算 我们知道质心也是点,跟每一个样本是一样的,所以这个问题相对简单只需要按照欧氏距离的公式来计算即可。
def cal_distance(point_A, point_B):
point_A = point_A.A
point_B = point_B.A
distance = np.sqrt(np.sum(np.power((point_A - point_B), 2)))
return distance2.3 数目时机更新质心位置 按照流程图的描述,更新质心位置需要在计算完每个样本到每个质心的距离之后,然后通过样本到其对应质心的距离的求和来更新质心位置。
2.4 如何判断样本归类发生变化 因为程序终止的条件是数据集中的样本的分类不再发生变化,反过来说就是只要数据集中存在一个样本的归类发生变化就需要重新计算。所以在死循环外需要建立一个 flag 来判断是否发生变化,然后在计算归类的时候需要有一个变量来记录该样本目前最优归类,需要一个变量来记录该样本上一次归类结果。
补充:所需要的数据结构 首先,对训练样本来说需要一个矩阵来存储。然后,因为需要记录每个样本的归类和该样本到其质心的距离,所以需要一个矩阵来存储归类和距离。最后,参与计算的还有质心矩阵,质心矩阵每一行代表一个质心,共 k 行。每一行结构根训练样本一样。
3、KMeans 算法
首先要生成分类矩阵
然后随机 k 个质心放入质心矩阵
用一个 flag 来标记循环
死循环判断是否有样本发生变化
两个循环对所有样本的所有质心计算记录
选择最优质心
判断样本质心变化,有则继续循环
更新质心坐标
完整代码
import math
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
def cal_distance(point_A, point_B):
"""计算两点之间的距离"""
point_A = point_A.A
point_B = point_B.A
distance = np.sqrt(np.sum(np.power((point_A - point_B), 2)))
return distance
def create_centers(data_matrix, k=4):
# 先把数计算出来降低时间复杂度
n, m = np.shape(data_matrix)
# 根据数据集创建随机质心 shape=[k,m] 保存质心的坐标
center_matrix = np.zeros(shape=(k, m))
for i in range(m):
min_val, max_val = min(data_matrix[:, i])[0, 0], max(data_matrix[:, i])[0, 0]
center_matrix[:, i] = np.array((min_val + (max_val - min_val) * np.random.rand(k, 1)))[:, 0]
center_matrix = np.mat(center_matrix)
return center_matrix
def my_k_means(data_matrix, k=4):
# 创建分类矩阵 [n,2] n 个样本 2 列用于存质心 index 和到其对应质心的 distance
cluster_matrix = np.zeros(shape=(len(data_matrix), 2))
# 创建随机质心矩阵
center_matrix = create_centers(data_matrix, k)
# 得到两个矩阵的 shape
center_matrix_n, center_matrix_m = np.shape(center_matrix)
data_matrix_n, data_matrix_m = np.shape(data_matrix)
# 是否有变化 flag
change_flag = True
# 直到没有变化为止结束
while change_flag:
change_flag = False
# 计算每一个点到每一个质心距离 取最小值归类
for i in range(data_matrix_n):
min_dist, min_index = math.inf, -1
for j in range(center_matrix_n):
# 计算距离
new_distance = cal_distance(data_matrix[i], center_matrix[j])
# 更新最近距离和质心 index
if min_dist > new_distance:
min_dist = new_distance
min_index = j
# 若质心有变化 更新质心 index
if min_index != cluster_matrix[i, 0]:
print("min_index != cluster_matrix[i, 0]", cluster_matrix[i, 0], min_index)
cluster_matrix[i, 0] = min_index
cluster_matrix[i, 1] = new_distance
change_flag = True
# 根据分类更新质心位置
for center in range(k):
# 从 data_matrix 中找到该类点 返回矩阵
# print(data_matrix[cluster_matrix[:, 0] == center])
# 对该矩阵求平均 axis 表方向 0 为列求平均 最后 [1,m]
# print("avg:", np.average(data_matrix[cluster_matrix[:, 0] == center], axis=0))
center_matrix[center] = np.average(data_matrix[cluster_matrix[:, 0] == center], axis=0).A[0]
return center_matrix
file_path = "data1.csv"
# 读数据
df = pd.read_csv(file_path)
# 画图
"""绘制数据分布图"""
plt.figure(figsize=(10, 10), dpi=180)
plt.scatter(x=df['x1'], y=df['x2'])
plt.savefig("origin_data.png")
# 转 df 为矩阵
data_matrix = np.mat(df)
# K-means 算法分类
center_matrix = my_k_means(data_matrix, 4)
"""绘制结果图"""
plt.figure(figsize=(10, 10), dpi=180)
plt.scatter(x=df['x1'], y=df['x2'], c='blue')
center_df = pd.DataFrame(center_matrix)
print(center_df)
plt.scatter(x=center_df.iloc[:, 0], y=center_df.iloc[:, 1], c='red', marker='x')
plt.savefig("after_kmeans_data.png")
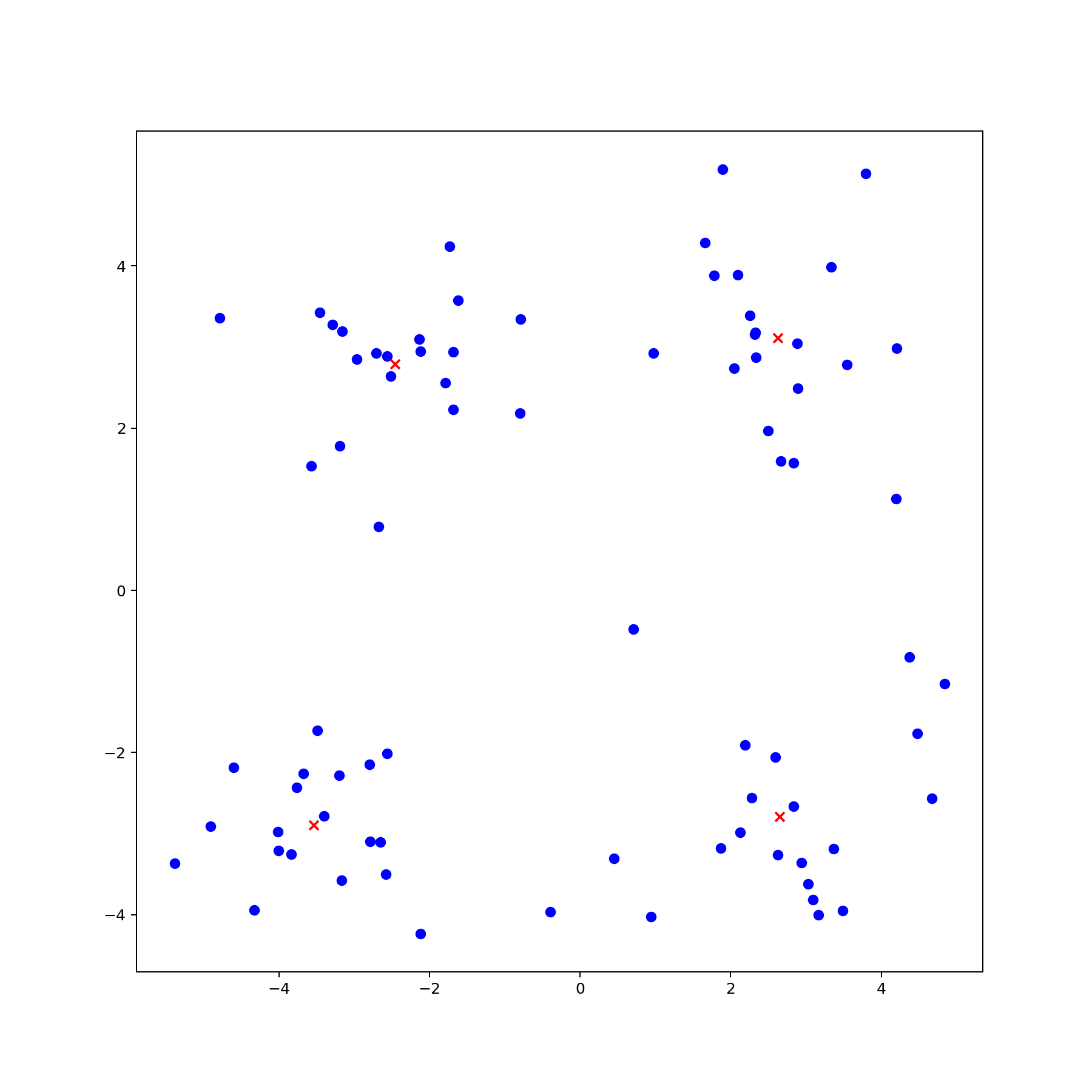
plt.show()最后的结果是这样的:
scikit-learn 里的 k-均值算法
scikit-learn 里的 k-均值算法由 sklearn.cluster.KMeans 类实现。下面通过一个简单的例子,来学习怎样在 scikit-learn 里使用 k-均值算法。
我们先生成一组包含两个特征的 200 个样本:
# 生成样本数据
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=200,
n_features=2,
centers=4,
cluster_std=1,
center_box=(-10.0, 10.0),
shuffle=True,
random_state=1)然后把样本画在二维坐标上,以便直观地观察:
plt.figure(figsize=(6, 4), dpi=144)
plt.xticks(())
plt.yticks(())
plt.scatter(X[:, 0], X[:, 1], s=20, marker='o')
plt.show()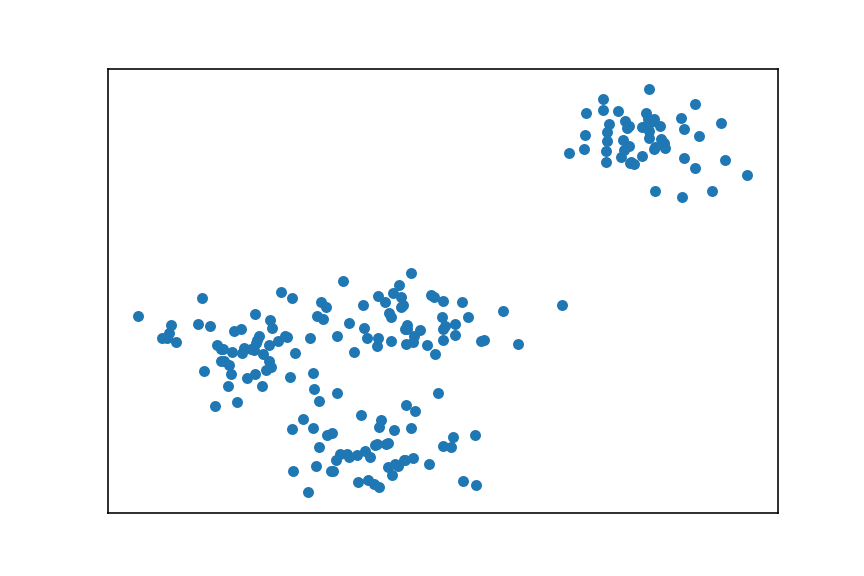
接着使用 KMeans 模型来拟合。我们设置类别数量为 3,并计算出其拟合后的成本:
# 聚类算法进行拟合,类别数量为 3
from sklearn.cluster import KMeans
n_clusters = 3
kmean = KMeans(n_clusters=n_clusters)
kmean.fit(X)
print("kmean: k={}, cost={}".format(n_clusters, int(kmean.score(X))))输出如下:
kmean: k=3, cost=-668KMeans.score() 函数计算 k-均值算法 拟合后的成本,用负数表示,其绝对值越大,说明成本越高。前面介绍过,k-均值算法成本的物理意义为 训练样例到其所属的聚类中心点的距离的平均值 ,在 scikit-learn 里,其计算成本的方法略有不同,它是计算训练样例到其所属的聚类中心点的 距离的总和 。
当然,我们还可以把分类后的样本及其所属的聚类中心都画出来,这样可以更直观地观察算法的拟合结果:
# 绘制拟合数据
labels = kmean.labels_
centers = kmean.cluster_centers_
markers = ['o', '^', '*']
colors = ['r', 'b', 'y']
plt.figure(figsize=(6, 4), dpi=144)
plt.xticks(())
plt.yticks(())
# 画样本
for c in range(n_clusters):
cluster = X[labels == c]
plt.scatter(cluster[:, 0], cluster[:, 1],
marker=markers[c], s=20, c=colors[c])
# 画出中心点
plt.scatter(centers[:, 0], centers[:, 1],
marker='o', c="white", alpha=0.9, s=300)
for i, c in enumerate(centers):
plt.scatter(c[0], c[1], marker='$%d$' % i, s=50, c=colors[i])
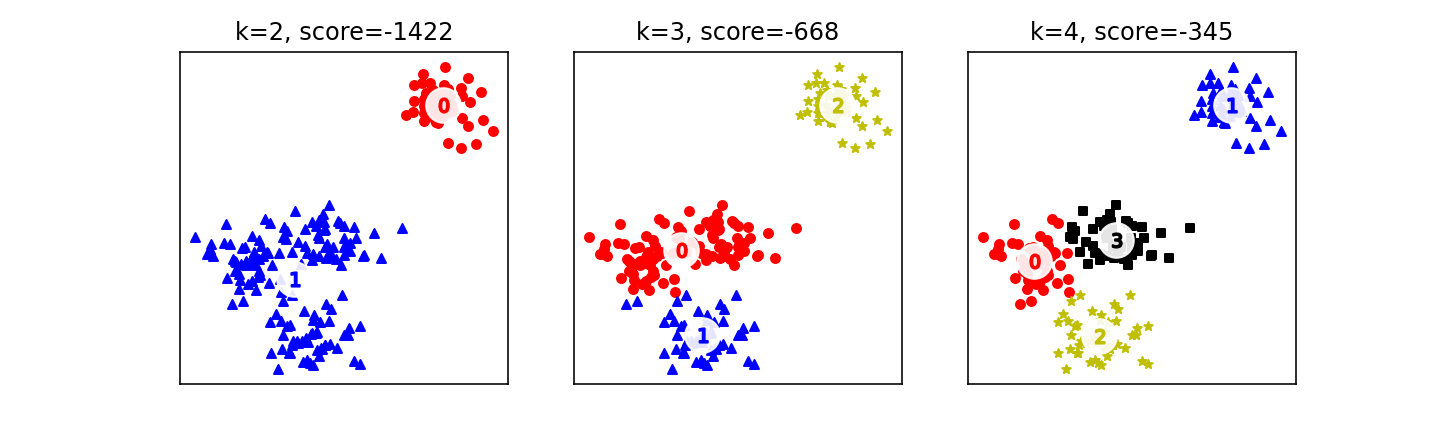
plt.show()前面说过,k-均值算法的一个关键参数是 k,即聚类个数。从技术角度来讲,k 值越大,算法成本越低,这个很容易理解。但从业务角度来看,不是 k 值越大越好。针对本节的例子,分别选择 k=2,3,4 这 3 种不同的聚类个数,来观察一下 k-均值算法最终拟合的结果及其成本值。
我们可以把画出 k-均值聚类结果的代码稍微改造一下,变成一个函数。这个函数会使用 k-均值算法来进行聚类拟合,同时会画出按照这个聚类个数拟合后的分类情况:
import matplotlib.pyplot as plt
import numpy as np
# 生成样本数据
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=200,
n_features=2,
centers=4,
cluster_std=1,
center_box=(-10.0, 10.0),
shuffle=True,
random_state=1)
# 绘制图像
plt.figure(figsize=(6, 4), dpi=144)
plt.xticks(())
plt.yticks(())
plt.scatter(X[:, 0], X[:, 1], s=20, marker='o')
plt.show()
# 聚类算法进行拟合
from sklearn.cluster import KMeans
def fit_plot_kmean_model(n_clusters, X):
plt.xticks(())
plt.yticks(())
# 使用 k-均值算法进行拟合
kmean = KMeans(n_clusters=n_clusters)
kmean.fit_predict(X)
labels = kmean.labels_
centers = kmean.cluster_centers_
markers = ['o', '^', '*', 's']
colors = ['r', 'b', 'y', 'k']
# 计算成本
score = kmean.score(X)
plt.title("k={}, score={}".format(n_clusters, (int)(score)))
# 画样本
for c in range(n_clusters):
cluster = X[labels == c]
plt.scatter(cluster[:, 0], cluster[:, 1],
marker=markers[c], s=20, c=colors[c])
# 画出中心点
plt.scatter(centers[:, 0], centers[:, 1],
marker='o', c="white", alpha=0.9, s=300)
for i, c in enumerate(centers):
plt.scatter(c[0], c[1], marker='$%d$' % i, s=50, c=colors[i])函数代码略微有点长,但通过注释应该不难理解函数的意图。函数接受两个参数,一个是聚类个数,即 k 的值,另一个是数据样本。有了这个函数,接下来的代码就简单了,可以很容易地分别对[2,3,4]3 种不同的 k 值情况进行聚类分析,并把聚类结果可视化。
n_clusters = [2, 3, 4]
plt.figure(figsize=(10, 3), dpi=144)
for i, c in enumerate(n_clusters):
plt.subplot(1, 3, i + 1)
fit_plot_kmean_model(c, X)
plt.show()输出如图
案例 - 文档聚类分析
接下来介绍如何使用 k-均值算法对文档进行聚类分析。假设有一个博客平台,用户在平台上发布博客,我们如何对博客进行聚类分析,以方便展示不同类别下的热门文章呢?
准备数据集
为了简化问题,避免进行中文分词,选择使用英文内容进行分词。
如何获取语料库?这些语料库是什么内容?格式是什么样的?
如何用数学来表达一个文档?
如何在 scikit-learn 里把文档导入并转化为对应的数学表达?
选择 sci.crypt、sci.electronics、sci.med 和 sci.space4 个类别的文档进行聚类分析
加载数据集
本次的任务:把 datasets/clustering/data 目录下的文档进行聚类分析。读者可能有疑问:这些文档不是按照文件夹已经分好类了吗?是的,这是人工标记了的数据。有了人工标记的数据,我们就可以检验 k-均值算法进行聚类分析的性能。
首先需要导入数据:
from sklearn.datasets import load_files
docs = load_files('clustering/data')
print("summary: {0} documents in {1} categories.".format(
len(docs.data), len(docs.target_names)))输出结果如下:
summary: 3949
documents in 4
categories.
done in 0.2530672550201416
seconds总共有 3949 篇文档,人工标记在 4 个类别里。接着把文档转化为 TF-IDF 向量:
from sklearn.feature_extraction.text import TfidfVectorizer
max_features = 20000
vectorizer = TfidfVectorizer(max_df=0.4,
min_df=2,
max_features=max_features,
encoding='latin-1')
X = vectorizer.fit_transform((d for d in docs.data))
print("n_samples: %d, n_features: %d" % X.shape)
print("number of non-zero features in sample [{0}]: {1}".format(
docs.filenames[0], X[0].getnnz()))这里需要注意 TfidfVectorizer 的几个参数的选择。其中,max_df=0.4 表示如果一个单词在 40% 的文档里都出现过,则认为这是一个高频词,对文档聚类没有帮助,在生成词典时就会剔除这个词。min_df=2 表示,如果一个单词的词频太低,只在两个以下 (包含两个) 的文档里出现,则也把这个单词从词典里剔除。max_features 可以进一步过滤词典的大小,它会根据 TF-IDF 权重从高到低进行排序,然后取前面权重高的单词构成词典。
上述代码的输出如下:
summary: 3949 documents in 4 categories.
n_samples: 3949, n_features: 20000
number of non-zero features in sample [clustering/data\sci.electronics\11902-54322]: 56从输出可知,我们的一篇文章构成的向量是一个稀疏向量,其大部分元素都为 0。这也容易理解,我们的词典大小为 20000 个,而示例文章中不重复的单词却只有 56 个。
文本聚类分析
接着前面的步骤,下面使用 KMeans 算法对文档进行聚类分析:
"""k-means 聚类"""
from sklearn.cluster import KMeans
t = time()
n_clusters = 4
kmean = KMeans(n_clusters=n_clusters,
max_iter=100,
tol=0.01,
verbose=1,
n_init=3)
kmean.fit(X)
print("kmean: k={}, cost={}".format(n_clusters, int(kmean.inertia_)))我们选择的聚类个数为 4 个。max_iter=100 表示最多进行 100 次 k-均值迭代。tol=0.1 表示中心点移动距离小于 0.1 时就认为算法已经收敛,停止迭代。verbose=1 表示输出迭代的过程信息。n_init=3 表示进行 3 次 k-均值运算后求平均值,前面介绍过,在算法刚开始迭代时,会随机选择聚类中心点,不同的中心点可能导致不同的收敛效果,因此多次运算求平均值的方法可以提供算法的稳定性。
由于开启了迭代过程信息展示,输出了较多的信息:
clustering documents ...
Initialization complete
Iteration 0, inertia 7548.338
Iteration 1, inertia 3845.294
...
Iteration 17, inertia 3821.018
Iteration 18, inertia 3821.016
Converged at iteration 18
Initialization complete
Iteration 0, inertia 7484.695
Iteration 1, inertia 3842.812
...
Iteration 52, inertia 3824.223
Iteration 53, inertia 3824.217
Converged at iteration 53
Initialization complete
Iteration 0, inertia 7535.568
Iteration 1, inertia 3847.240
...
Iteration 22, inertia 3822.391
Iteration 23, inertia 3822.389
Converged at iteration 23
kmean: k=4, cost=3821
done in 2.81433701515 seconds从输出信息中可以看到,总共进行了 3 次 k-均值聚类分析,分别做了 195424 次迭代后收敛。这样就把 3949 个文档进行自动分类了。kmean.labels_里保存的就是这些文档的类别信息。如我们所预料,len(kmean.labels_) 的值是 3949,还可以通过 kmean.labels_[:100]查看前 100 个文档的分类情况。
array([0, 0, 0, 0, 0, 0, 1, 2, 3, 0, 0, 0, 0, 0, 3, 0, 1, 0, 0, 0, 3,0,3,
0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 2, 0, 0, 2, 0, 1,3,3,
0, 3, 0, 0, 1, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 1, 2, 3, 0, 0, 0,0,1,
0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 3, 3, 0,0,0,
0, 1, 1, 0, 0, 3, 3, 2], dtype=int32)我们还可以查看 1000~1010 这 10 个文档的聚类情况及其对应的文件名:
kmean.labels_[1000:1010]
array([1, 1, 1, 0, 3, 0, 3, 1, 0, 0], dtype=int32)接着查看对应的文件名:
print(docs.filenames[1000:1010])
['clustering/data\\sci.crypt\\10888-15289'
'clustering/data\\sci.crypt\\11490-15880'
'clustering/data\\sci.crypt\\11270-15346'
'clustering/data\\sci.electronics\\12383-53525'
'clustering/data\\sci.space\\13826-60862'
'clustering/data\\sci.electronics\\11631-54106'
'clustering/data\\sci.space\\14235-61437'
'clustering/data\\sci.crypt\\11508-15928'
'clustering/data\\sci.space\\13593-60824'
'clustering/data\\sci.electronics\\12304-52801']对比两个输出可以看到,这 10 个文档基本上正确地归类了。需要说明的是,这里类别 1 表示 sci.crypt,但这不是必然的对应关系。重新进行一次聚类分析可能就不是这个对应关系了。我们还可以选择 k 为 3 或 2 进行聚类分析,从而彻底打乱原来标记的类别的关系。
到这里,有读者可能比较好奇:在进行聚类分析过程中,哪些单词的权重最高,从而较容易地决定一个文章的类别?我们可以查看每种类别文档中,其权限最高的 10 个单词分别是什么:
"""权限最高的10个单词"""
print("Top terms per cluster:")
order_centroids = kmean.cluster_centers_.argsort()[:, ::-1]
terms = vectorizer.get_feature_names()
for i in range(n_clusters):
print("Cluster %d:" % i, end='')
for ind in order_centroids[i, :10]:
print(' %s' % terms[ind], end='')
print()理解这段代码的关键在于 argsort() 函数,它的作用是把一个 Numpy 数组进行升序排列,返回的是排序后的索引。例如下面的示例代码:
a = np.array([10, 30, 20, 40])
a.argsort()其输出如下:
array([0, 2, 1, 3])即索引为 0 的元素 (10) 最小,其次是索引为 2 的元素 (20),再次是索引为 1 的元素 (30),最大的是索引为 3 的元素 (40) 。而[::-1]运算是把升序变为降序,例如上述示例代码里 a.argsort()[::-1]的输出为 array([3,1,2,0])。
回到我们的代码里,由于 kmean.cluster_centers_是二维数组,因此 kmean.cluster_centers_.argsort() [:,::-1]语句的含义就是把聚类中心点的不同分量,按照从大到小的顺序进行排序,并且把排序后的元素索引保存在二维数组 order_centroids 里。vectorizer.get_feature_names() 将得到我们的词典单词,根据索引即可得到每个类别里权重最高的那些单词了。
上述代码在计算机上的输出如下:
Top terms per cluster:
Cluster 0: space henry nasa toronto pat shuttle zoo moon gov orbit
Cluster 1: any my know by me your anyone do will like
Cluster 2: my she msg pitt he gordon her has geb banks
Cluster 3: key clipper chip encryption government keys will escrow we algorithm从上述权重最高的单词可以看出,Cluster 0 的效果不好,因为那些单词太没特点了,可以是任何类别。而 Cluster 1 的效果比较高,一看就知道是关于网络安全的,对应的是 sci.crypt 这个类别。从高权重的单词里也可以猜得出来,Cluster 2 和 Cluster 3 对应的分别是 sci.med 和 sci.space。
聚类算法性能评估
聚类性能评估比较复杂,不像分类问题那样直观。针对分类问题,我们可以直接计算被错误分类的样本数量,这样可以直接算出分类算法的准确率。聚类问题不能使用绝对数量的方法进行性能评估,直接的原因是,聚类分析后的类别与原来己标记的类别之间不存在必然的一一对应关系。更典型地,针对 k-均值算法,我们可以选择 k 的数值不等于己标记的类别个数。
之前介绍过“熵”的概念,它是信息论中最重要的基础概念。熵表示一个系统的有序程度,而聚类问题的性能评估,就是对比经过聚类算法处理后的数据的有序程度,与人工标记的类别的有序程度之间的差异。接下来将介绍几个常用的聚类算法性能评估指标。
Adjust Rand Index
Adjust Rand Index 是一种衡量两个序列相似性的算法。它的优点是,针对两个随机序列,它的值为负数或接近于 0,而针对两个结构相同的序列,它的值接近于 1。而且对类别标签不敏感。下面来看一个简单的例子:
import numpy as np
from sklearn import metrics
label_true = np.random.randint(1, 4, 6)
label_pred = np.random.randint(1, 4, 6)
print("Adjusted Rand-Index for random sample: %.3f"
% metrics.adjusted_rand_score(label_true, label_pred))
label_true = [1, 1, 3, 3, 2, 2]
label_pred = [3, 3, 2, 2, 1, 1]
print("Adjusted Rand-Index for same structure sample: %.3f"
% metrics.adjusted_rand_score(label_true, label_pred))计算机上的输出如下:
Adjusted Rand-Index for random sample: -0.023
Adjusted Rand-Index for same structure sample: 1.000齐次性和完整性
根据条件熵分析,可以得到另外两个衡量聚类算法性能的指标,分别是齐次性 (homogeneity) 和完整性 (completeness) 。齐次性表示一个聚类元素只由一种类别的元素组成。完整性表示给定的已标记的类别,全部分配到一个聚类里。它们的值均介于[0,1]之间。下面通过一个简单的例子来解释这两个概念:
from sklearn import metrics
label_true = [1, 1, 2, 2]
label_pred = [2, 2, 1, 1]
print("Homogeneity score for same structure sample: %.3f"
% metrics.homogeneity_score(label_true, label_pred))
label_true = [1, 1, 2, 2]
label_pred = [0, 1, 2, 3]
print("Homogeneity score for each cluster come from only one class: %.3f"
% metrics.homogeneity_score(label_true, label_pred))
label_true = [1, 1, 2, 2]
label_pred = [1, 2, 1, 2]
print("Homogeneity score for each cluster come from two class: %.3f"
% metrics.homogeneity_score(label_true, label_pred))
label_true = np.random.randint(1, 4, 6)
label_pred = np.random.randint(1, 4, 6)
print("Homogeneity score for random sample: %.3f"
% metrics.homogeneity_score(label_true, label_pred))计算机上的输出如下:
Homogeneity score for same structure sample: 1.000
Homogeneity score for each cluster come from only one class: 1.000
Homogeneity score for each cluster come from two class: 0.000
Homogeneity score for random sample: 0.633针对第 1 组序列,其结构相同,因此其齐次性输出为 1,表示完全一致。奇怪的事情来了,第 2 组样本[1,1,2,2]和[0,1,2,3]为什么输出也为 1 呢?答案就在齐次性的定义上,聚类元素只由一种已标记的类别元素组成时,其值为 1。在我们的例子里,已标记为 2 个类别,而输出了 4 个聚类,这样就满足每个聚类元素均来自一种已标记的类别元素这一条件。同样的道理,针对第 3 组样本,由于每个聚类元素都来自 2 个类别的元素,因此其值为 0;而针对随机的元素序列,它不为 0,这是与 Adjust Rand Index 不同的地方。
接下来看一组完整性的例子:
from sklearn import metrics
label_true = [1, 1, 2, 2]
label_pred = [2, 2, 1, 1]
print("Completeness score for same structure sample: %.3f"
% metrics.completeness_score(label_true, label_pred))
label_true = [0, 1, 2, 3]
label_pred = [1, 1, 2, 2]
print("Completeness score for each class assign to only one cluster: %.3f"
% metrics.completeness_score(label_true, label_pred))
label_true = [1, 1, 2, 2]
label_pred = [1, 2, 1, 2]
print("Completeness score for each class assign to two class: %.3f"
% metrics.completeness_score(label_true, label_pred))
label_true = np.random.randint(1, 4, 6)
label_pred = np.random.randint(1, 4, 6)
print("Completeness score for random sample: %.3f"
% metrics.completeness_score(label_true, label_pred))计算机上的输出如下:
Completeness score for same structure sample: 1.000
Completeness score for each class assign to only one cluster: 1.000
Completeness score for each class assign to two class: 0.000
Completeness score for random sample: 0.159针对第 1 组序列,其结构相同,输出为 1。针对第 2 组序列,由于符合完整性的定义,即每个类别的元素都被分配进了同一个聚类里,因此其完整性也为 1。针对第 3 组序列,每个类别的元素都被分配进了两个不同的聚类里,因此其完整性为 0。和齐次性一样,它对随机类别的判断能力也比较弱。
从上面的例子中可以看出,齐次性和完整性是一组互补的关系,我们可以把两个指标综合起来,称为 V-measure 分数。下面来看一个简单的例子:
from sklearn import metrics
label_true = [1, 1, 2, 2]
label_pred = [2, 2, 1, 1]
print("V-measure score for same structure sample: %.3f"
% metrics.v_measure_score(label_true, label_pred))
label_true = [0, 1, 2, 3]
label_pred = [1, 1, 2, 2]
print("V-measure score for each class assign to only one cluster: %.3f"
% metrics.v_measure_score(label_true, label_pred))
print("V-measure score for each class assign to only one cluster: %.3f"
% metrics.v_measure_score(label_pred, label_true))
label_true = [1, 1, 2, 2]
label_pred = [1, 2, 1, 2]
print("V-measure score for each class assign to two class: %.3f"
% metrics.v_measure_score(label_true, label_pred))笔者计算机上的输出如下:
V-measure score for same structure sample: 1.000
V-measure score for each class assign to only one cluster: 0.667
V-measure score for each class assign to only one cluster: 0.667
V-measure score for each class assign to two class: 0.000针对第 1 组序列,其结构相同,V-measure 输出的值也为 1,表示同时满足齐次性和完整性。第 2 行和第 3 行的输出,表明 V-measure 符合对称性法则。
轮廓系数
上面介绍的聚类性能评估方法都需要有已标记的类别数据,这个在实践中是很难做到的。如果已经标记了数据,就会直接用有监督的学习算法,而无监督学习算法的最大优点就是不需要对数据集进行标记。轮廓系数可以在不需要已标记的数据集的前提下,对聚类算法的性能进行评估。
轮廓系数由以下两个指标构成。
a:一个样本与其所在相同聚类的平均距离;
b:一个样本与其距离最近的下一个聚类里的点的平均距离。
则针对这个样本,其轮廓系数 s 的值为:
针对一个数据集,其轮廓系数 s 为其所有样本的轮廓系数的平均值。轮廓系数的数值介于[-1,1]之间,-1 表示完全错误的聚类,1 表示完美的聚类,0 表示聚类重叠。
针对前面的例子,可以分别计算本节介绍的几个聚类算法性能评估指标,综合来看聚类算法的性能:
from sklearn import metrics
labels = docs.target
print("Homogeneity: %0.3f" % metrics.homogeneity_score(labels, kmean.labels_))
print("Completeness: %0.3f" % metrics.completeness_score(labels, kmean.labels_))
print("V-measure: %0.3f" % metrics.v_measure_score(labels, kmean.labels_))
print("Adjusted Rand-Index: %.3f" % metrics.adjusted_rand_score(labels, kmean.labels_))
print("Silhouette Coefficient: %0.3f" % metrics.silhouette_score(X, kmean.labels_, sample_size=1000))计算机上的输出如下:
Homogeneity: 0.351
Completeness: 0.505
V-measure: 0.414
Adjusted Rand-Index: 0.228
Silhouette Coefficient: 0.004这些数值是好是坏呢?坦白讲,只能算为一般。读者可以结合上述介绍的指标的含义,理解这些数值背后表达的意义。可能的一个原因是数据集质量不高,感兴趣的读者可以阅读原始的语料库,检验一下如果通过人工标记,是否能够标记出这些文章的正确分类。另外,针对 Cluster 0 的前 10 大 TF-IDF 权重的单词 my、any、me、by、know、your、some、do、so、has,这些都是没有特征的单词,即使人工标记,也无法判断这些单词应该属于哪种类别的文章。