朴素贝叶斯

朴素贝叶斯算法是有监督的学习算法，解决的是分类问题，如客户是否流失、是否值得投资、信用等级评定等多分类问题。** 该算法的优点在于简单易懂、学习效率高、在某些领域的分类问题中能够与决策树、神经网络相媲美。** 但由于该算法以自变量之间的独立（条件特征独立）性和连续变量的正态性假设为前提，就会导致算法精度在某种程度上受影响。

朴素贝叶斯分类最适合的场景就是文本分类、情感分析和垃圾邮件识别。其中情感分析和垃圾邮件识别都是通过文本来进行判断。从这里你能看出来，这三个场景本质上都是文本分类，这也是朴素贝叶斯最擅长的地方。所以朴素贝叶斯也常用于自然语言处理 NLP 的工具。

贝叶斯决策理论

假设现在我们有一个数据集，它由两类数据组成，数据分布如下图所示：

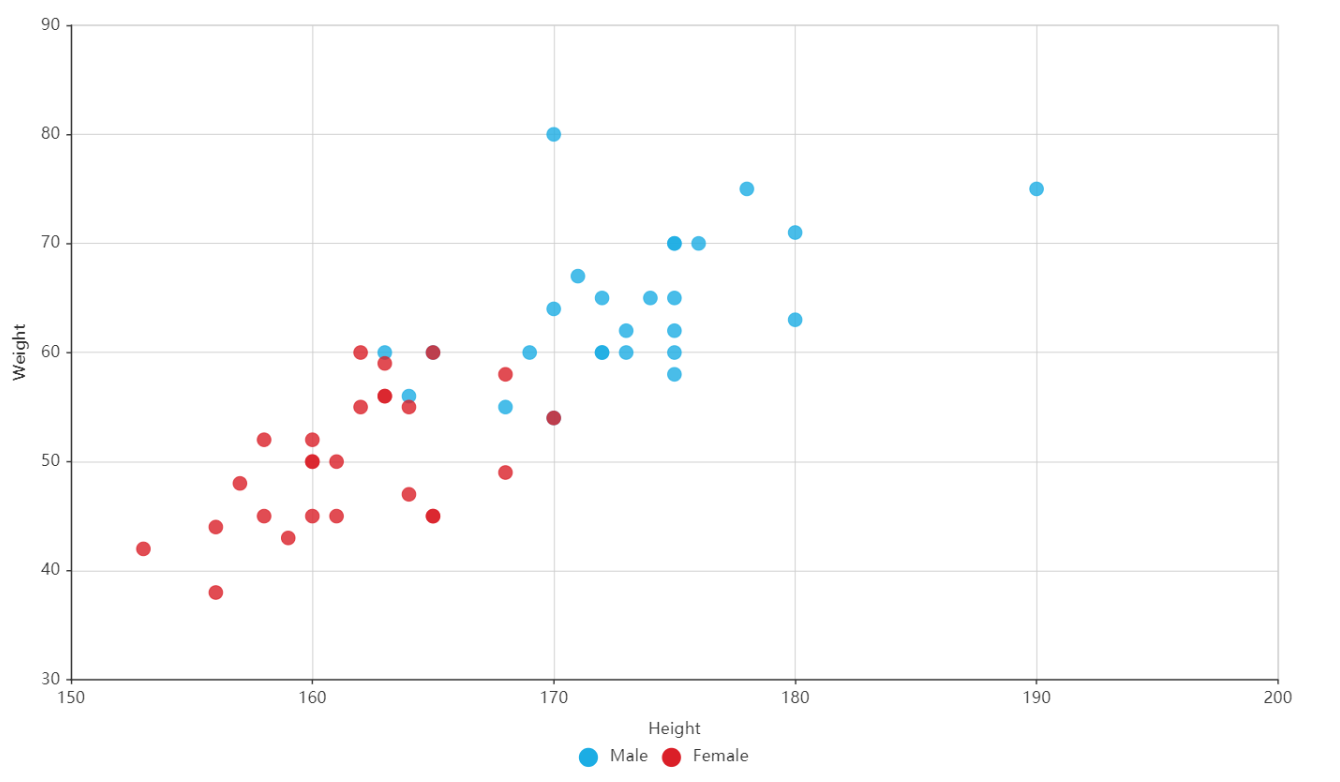
我们现在用 $p1(x,y)$ 表示数据点 $(x,y)$ 属于类别 1(图中红色圆点表示的类别) 的概率，用 $p2(x,y)$ 表示数据点 $(x,y)$ 属于类别 2(图中蓝色三角形表示的类别) 的概率，那么对于一个新数据点 (x,y)，可以用下面的规则来判断它的类别：

• 如果 $p_1(x,y)>p_2(x,y)$ ，那么类别为 1
• 如果 $p_1(x,y)<p_2(x,y)$，那么类别为 2

也就是说，我们会选择高概率对应的类别。这就是贝叶斯决策理论的核心思想，即选择具有最高概率的决策。已经了解了贝叶斯决策理论的核心思想，那么接下来，就是学习如何计算 p1 和 p2 概率。

条件概率

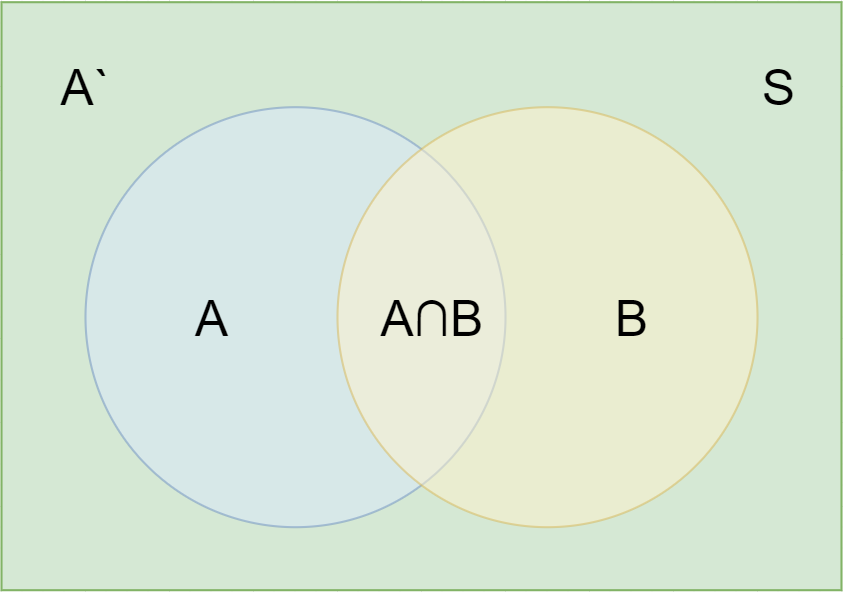
在学习计算 p1 和 p2 概率之前，我们需要了解什么是条件概率 (Conditional probability)，就是指在事件 B 发生的情况下，事件 A 发生的概率，用 P(A|B) 来表示。

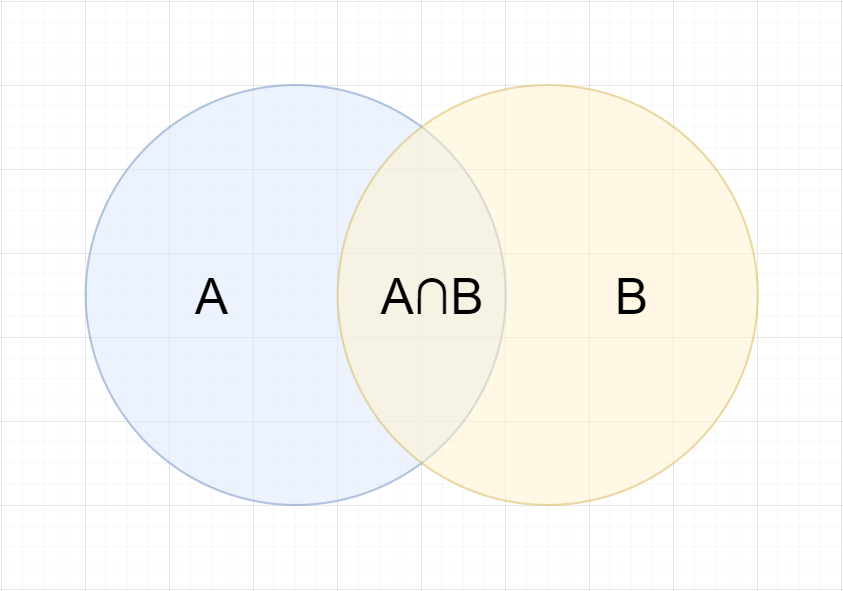
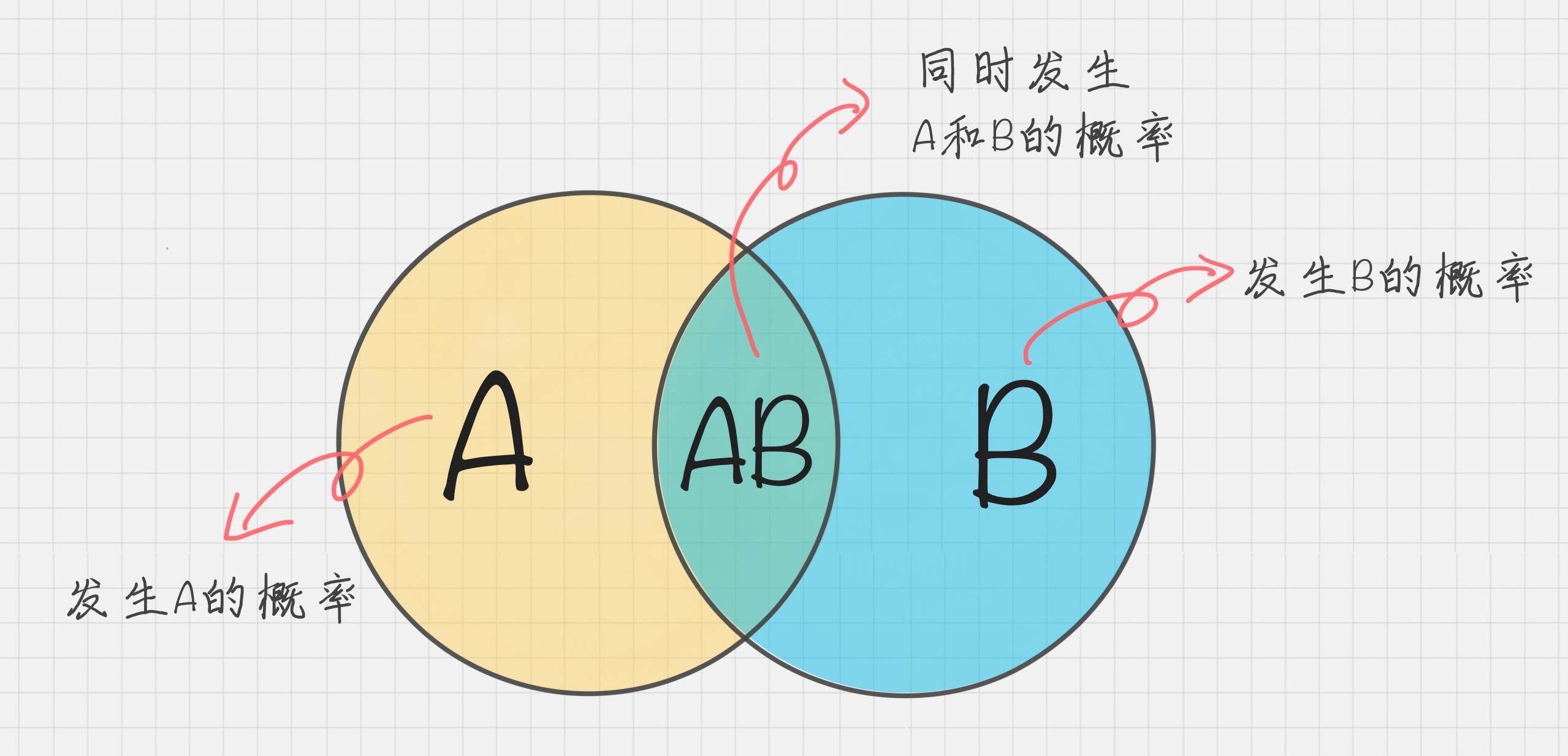
根据文氏图，可以很清楚地看到在事件 B 发生的情况下，事件 A 发生的概率就是 P(A∩B) 除以 P(B)。

$$P(A|B)=\frac{P(A\cap B)}{P(B)}$$

因此

$$P(A\cap B)=P(A|B)P(B)$$

同理可得

$$P(A\cap B)=P(B|A)P(A)$$

所以

$$P(B|A)P(A)=P(A|B)P(B)$$

即

$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$

这就是条件概率公式

全概率公式 (了解)

除了条件概率以外，在计算 p1 和 p2 的时候，还要用到全概率公式，因此，这里继续推导全概率公式。

假定样本空间 S，是两个事件 A 与 A'的和。

即

$$P(B)=P(B\cap A)+P(B\cap A\prime )$$

在上一节的推导当中，我们已知

$$P(A\cap B)=P(B|A)P(A)$$

所以，

$$P(B)=P(B|A)P(A)+P(B|A\prime )P(A\prime )$$

这就是全概率公式。它的含义是，如果 A 和 A'构成样本空间的一个划分，那么事件 B 的概率，就等于 A 和 A'的概率分别乘以 B 对这两个事件的条件概率之和。

将这个公式代入上一节的条件概率公式，就得到了条件概率的另一种写法：

$$\begin{gathered} P(A|B)=\frac{P(B|A)P(A)}{ \\ P(B|A)P(A)+P(B|A\prime )P(A\prime )} \end{gathered}$$

贝叶斯推断

对条件概率公式进行变形，可以得到如下形式：

$$P(A|B)=P(A)\frac{P(B|A)}{P(B)}$$

我们把 P(A) 称为"先验概率"（Prior probability），即在 B 事件发生之前，我们对 A 事件概率的一个判断。

P(A|B) 称为"后验概率"（Posterior probability），即在 B 事件发生之后，我们对 A 事件概率的重新评估。

P(B|A)/P(B) 称为"可能性函数"（Likelyhood），这是一个调整因子，使得预估概率更接近真实概率。

所以，条件概率可以理解成下面的式子：

后验概率　＝　先验概率 ｘ 调整因子

这就是贝叶斯推断的含义。我们先预估一个"先验概率"，然后加入实验结果，看这个实验到底是增强还是削弱了"先验概率" ，由此得到更接近事实的"后验概率"。

在这里，如果"可能性函数"P(B|A)/P(B)>1，意味着"先验概率"被增强，事件 A 的发生的可能性变大；如果"可能性函数"=1，意味着 B 事件无助于判断事件 A 的可能性；如果"可能性函数"<1，意味着"先验概率"被削弱，事件 A 的可能性变小。

概率定义

概率定义为⼀件事情发⽣的可能性 扔出⼀个硬币，结果头像朝上 P(X) : 取值在[0, 1]

	职业	体型	女神是否喜欢
1	程序员	超重	不喜欢
2	产品	匀称	喜欢
3	程序员	匀称	喜欢
4	程序员	超重	喜欢
5	美工	匀称	不喜欢
6	美工	超重	不喜欢
7	产品	匀称	喜欢

问题如下：

1. ⼥神喜欢的概率？
2. 职业是程序员并且体型匀称的概率？
3. 在⼥神喜欢的条件下，职业是程序员的概率？
4. 在⼥神喜欢的条件下，职业是程序员、体重超重的概率？

P(喜欢) = 4/7
P(程序员, 匀称) = 1/7(联合概率)
P(程序员|喜欢) = 2/4 = 1/2(条件概率)
P(程序员, 超重|喜欢) = 1/4

思考题：在⼩明是产品经理并且体重超重的情况下，如何计算⼩明被⼥神喜欢的概率？ 即 P(喜欢 | 产品，超重) = ？ 此时我们需要⽤到朴素⻉叶斯进⾏求解，在讲解⻉叶斯公式之前，⾸先复习⼀下联合概率、条件概率和相互独⽴的概念。

联合概率、条件概率与相互独立

联合概率：包含多个条件，且所有条件同时成⽴的概率 记作：P(A,B) 条件概率：就是事件 A 在另外⼀个事件 B 已经发⽣条件下的发⽣概率 记作：P(A|B) 相互独⽴：如果 P(A, B) = P(A)P(B)，则称事件 A 与事件 B 相互独⽴。

贝叶斯公式

$$P(C|W)=\frac{P(W|C)P(C)}{P(W)}$$

注：W 为给定文档的特征值（频数统计，预测文档提供）,C 为文档类别

案例计算

那么思考题就可以套⽤⻉叶斯公式这样来解决：

P(喜欢 | 产品，超重) = P(产品，超重 | 喜欢)P(喜欢)/P(产品，超重)

上式中，

• P(产品，超重 | 喜欢) 和 P(产品，超重) 的结果均为 0，导致⽆法计算结果。这是因为我们的样本量太少了，不具有代表 性。
• 本来现实⽣活中，肯定是存在职业是产品经理并且体重超重的⼈的，P(产品，超重) 不可能为 0；
• ⽽且事件“职业是产品经理”和事件“体重超重”通常被认为是相互独⽴的事件，但是，根据我们有限的 7 个样本计算“P(产品，超重) = P( 产品)P(超重)”不成⽴。

⽽朴素⻉叶斯可以帮助我们解决这个问题。

• 朴素贝叶斯，简单理解，就是假定了特征与特征之间相互独⽴的⻉叶斯公式。
• 也就是说，朴素贝叶斯，之所以朴素，就在于假定了特征与特征相互独⽴。

所以，思考题如果按照朴素⻉叶斯的思路来解决，就可以是

P(产品, 超重) = P(产品) * P(超重) = 2/7 * 3/7 = 6/49
p(产品, 超重|喜欢) = P(产品|喜欢) * P(超重|喜欢) = 1/2 * 1/4 = 1/8
P(喜欢|产品, 超重) = P(产品, 超重|喜欢) * P(喜欢)/P(产品, 超重) = 1/8 * 4/7 / 6/49 = 7/12

那么这个公式如果应⽤在⽂章分类的场景当中，我们可以这样看：

公式可以理解为

$$P(C|F1,F2,...)=\frac{P(F1,F2,...|C)}{P(F1,F2,...)}$$

其中 C 可以是不同类别

公式分为三个部分

• P(C)：每个文档类别的概率（某个文档类别数/总文档数量）
• P(W│C)：给定类别下特征（被预测⽂档中出现的词）的概率
  • 计算⽅法：P(F1│C)=Ni/N（训练⽂档中去计算）
    • Ni 为该 F1 词在 C 类别所有⽂档中出现的次数
    • N 为所属类别 C 下的⽂档所有词出现的次数和
• P(F1,F2,…) 预测⽂档中每个词的概率

如果计算两个类别概率⽐较：

所以我们只要比较前面的大小，就可以得出谁的概率大

文章分类计算

需求：通过前四个训练样本（⽂章），判断第五篇⽂章，是否属于 China 类

	文档 ID	文档中的词	输入 c=China 类
训练集	1	Chinese Beijing Chinese	Yes
	2	Chinese Chinese Shanghai	Yes
	3	Chinese Macao	Yes
	4	Tokyo Japan Chinese	No
测试集	5	Chinese Chinese Chinese Tokyo Japan	?

计算结果

P(C|Chinese, Chinese, Chinese, Tokyo, Japan) -->
P(Chinese, Chinese, Chinese, Tokyo, Japan|C) * P(C) / P(Chinese, Chinese, Chinese, Tokyo, Japan)
=
P(Chinese|C)^3 * P(Tokyo|C) * P(Japan|C) * P(C) / [P(Chinese)^3 * P(Tokyo) * P(Japan)]
# 这个⽂章是需要计算是不是China类，是或者不是最后的分⺟值都相同:
# ⾸先计算是China类的概率:

P(Chinese|C) = 5/8
P(Tokyo|C) = 0/8
P(Japan|C) = 0/8

# 接着计算不是China类的概率:
P(Chinese|C) = 1/3
P(Tokyo|C) = 1/3
P(Japan|C) = 1/3

问题：从上面的例子我们得到 P(TokyolC) 和 P(JapanIC) 都为 0，这是不合理的，如果词频列表里面有很多出现次数都为 0，很可能计算结果都为零。

解决方法：拉普拉斯平滑系数

$$P(F1|C)=\frac{Ni+\alpha }{N+\alpha m}$$

a 为指定的系数一般为 1，m 为训练文档中统计出的特征词个数

#这个文章是需要计算是不是China类:

首先计算是China类的概率: 0.0003
	P(Chinese|C) = 5/8 --> 6/14
	P(Tokyo|C) = 0/8 --> 1/14
	P( Japan|C) = 0/8 --> 1/14

接着计算不是China类的概率: 0. 0001
	P(Chinese|C) = 1/3 --> (经过拉普拉斯平滑系数处理) 2/9
	P(Tokyo|C) = 1/3 --> 2/9
	P(Japan|C) = 1/3 --> 2/9

案例：商品评论情感分析

应用朴素贝叶斯 API 实现商品评论情感分析

学习目标

api 介绍

sklearn.naive_ _bayes.MultinomialNB(alpha =|1.0)

• 朴素贝叶斯分类
• alpha:拉普拉斯平滑系数

商品评论情感分析

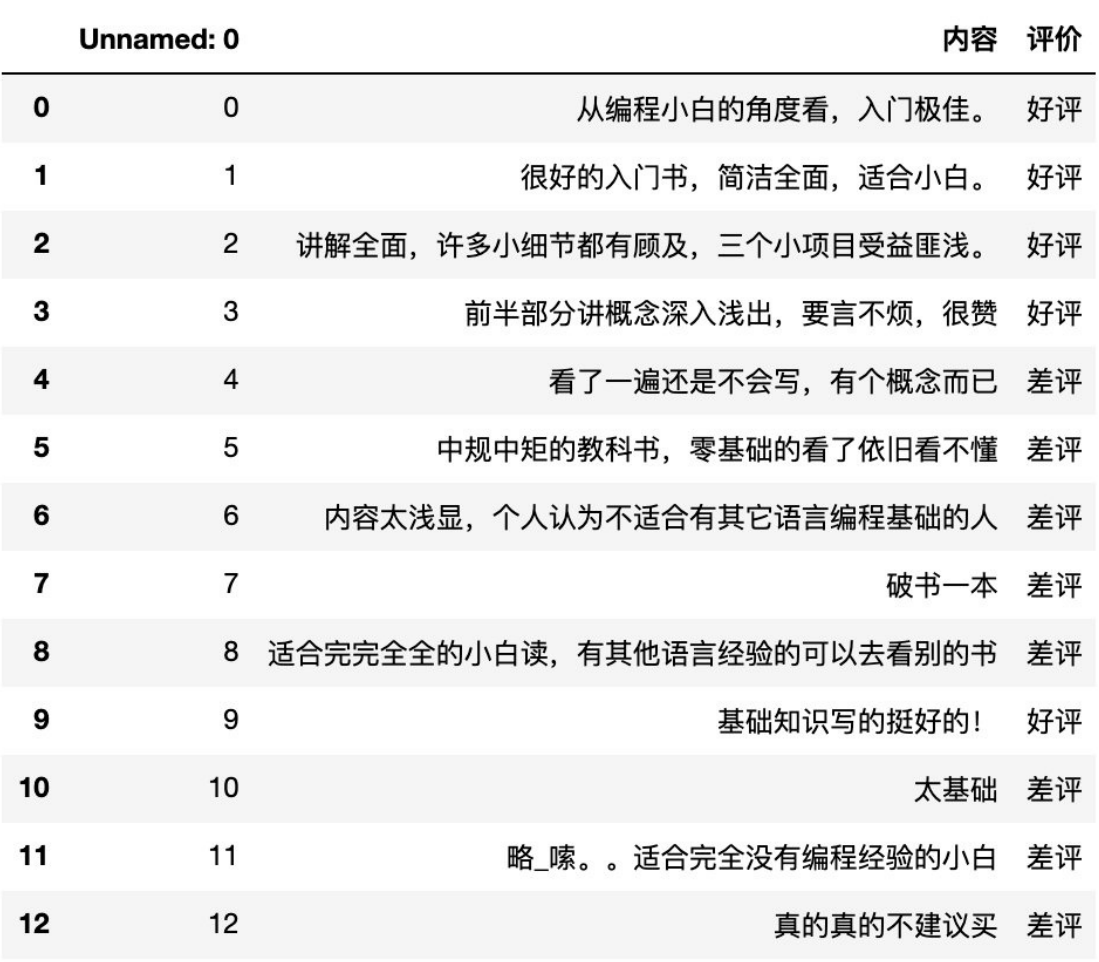
步骤分析

• 1）获取数据
• 2）数据基本处理
  • 2.1）取出内容列，对数据进⾏分析
  • 2.2）判定评判标准
  • 2.3）选择停⽤词
  • 2.4）把内容处理，转化成标准格式
  • 2.5）统计词的个数
  • 2.6）准备训练集和测试集
• 3）模型训练
• 4）模型评估

案例：中文文档分类

对中文文档分类的练习题吧。

数据说明：

文档共有 4 中类型：女性、体育、文学、校园；

训练集放到 train 文件夹里，测试集放到 test 文件夹里，停用词放到 stop 文件夹里。

请使用朴素贝叶斯分类对训练集进行训练，并对测试集进行验证，并给出测试集的准确率。

# 中文文本分类
import os
import jieba
import warnings
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn import metrics

warnings.filterwarnings('ignore')


def cut_words(file_path):
    """
    对文本进行切词
    :param file_path: txt 文本路径
    :return: 用空格分词的字符串
    """
    text_with_spaces = ''
    text = open(file_path, 'r', encoding='gb18030').read()
    textcut = jieba.cut(text)
    for word in textcut:
        text_with_spaces += word + ' '
    return text_with_spaces


def loadfile(file_dir, label):
    """
    将路径下的所有文件加载
    :param file_dir: 保存 txt 文件目录
    :param label: 文档标签
    :return: 分词后的文档列表和标签
    """
    file_list = os.listdir(file_dir)
    words_list = []
    labels_list = []
    for file in file_list:
        file_path = file_dir + '/' + file
        words_list.append(cut_words(file_path))
        labels_list.append(label)
    return words_list, labels_list


# 训练数据
train_words_list1, train_labels1 = loadfile('text classification/train/女性', '女性')
train_words_list2, train_labels2 = loadfile('text classification/train/体育', '体育')
train_words_list3, train_labels3 = loadfile('text classification/train/文学', '文学')
train_words_list4, train_labels4 = loadfile('text classification/train/校园', '校园')

train_words_list = train_words_list1 + train_words_list2 + train_words_list3 + train_words_list4
train_labels = train_labels1 + train_labels2 + train_labels3 + train_labels4

# 测试数据
test_words_list1, test_labels1 = loadfile('text classification/test/女性', '女性')
test_words_list2, test_labels2 = loadfile('text classification/test/体育', '体育')
test_words_list3, test_labels3 = loadfile('text classification/test/文学', '文学')
test_words_list4, test_labels4 = loadfile('text classification/test/校园', '校园')

test_words_list = test_words_list1 + test_words_list2 + test_words_list3 + test_words_list4
test_labels = test_labels1 + test_labels2 + test_labels3 + test_labels4

stop_words = open('text classification/stop/stopword.txt', 'r', encoding='utf-8').read()
stop_words = stop_words.encode('utf-8').decode('utf-8-sig')  # 列表头部\ufeff 处理
stop_words = stop_words.split('\n')  # 根据分隔符分隔

# 计算单词权重
tf = TfidfVectorizer(stop_words=stop_words, max_df=0.5)

train_features = tf.fit_transform(train_words_list)
# 上面 fit 过了，这里 transform
test_features = tf.transform(test_words_list)

# 多项式贝叶斯分类器

clf = MultinomialNB(alpha=0.001).fit(train_features, train_labels)
predicted_labels = clf.predict(test_features)

# 计算准确率
print('准确率为：', metrics.accuracy_score(test_labels, predicted_labels))

朴素贝叶斯算法总结

朴素贝叶斯优缺点

• 优点：
  • 朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率
  • 对缺失数据不太敏感，算法也比较简单，常用于文本分类
  • 分类准确度高，速度快
• 缺点：
  • 由于使用了样本属性独立性的假设，所以如果特征属性有关联时其效果不好
  • 需要计算先验概率，而先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳;

朴素贝叶斯内容汇总

NB 的原理

朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。

• 对于给定的待分类项 x，通过学习到的模型计算后验概率分布，
• 即：在此项出现的条件下各个目标类别出现的概率，将后验概率最大的类作为 x 所属的类别。

**朴素贝叶斯朴素在哪里？ **

在计算条件概率分布 $P(X=x|Y=c_k)$ 时，NB 引入了一个很强的条件独立假设，即，当 Y 确定时，X 的各个特征分量取值之间相互独立。

为什么引入条件独立性假设？

为了避免贝叶斯定理求解时面临的组合爆炸、样本稀疏问题。 假设条件概率分为

$$\begin{gathered} P(X=x|Y=c_k)=P \\ ⟮ \\ {X}^{(1)}=x^{(1)},...X^{(n)}=x^{(n)}|Y=c_k⟯ \end{gathered}$$

其中 $x^{(j)}$ 可能取值有 $S_j$ 个，$j= 1,2...n, $ $Y$ 可能取值有 $K$ 个，那么参数个数为 $$K\prod_{j=1}^{n}S_{j}$$ 个，这就导致条件概率分布的参数数量为指数级别。

在估计条件概率 P(X|Y) 时出现概率为 0 的情况怎么办？

解决这一问题的方法是采用贝叶斯估计。 简单来说，引入 λ ,

• 当 λ=0 时，就是普通的极大似然估计;
• 当 λ=1 时称为 拉普拉斯平滑。

为什么属性独立性假设在实际情况中很难成立，但朴素贝叶斯仍能取得较好的效果？

• 人们在使用分类器之前，首先做的第一步 (也是最重要的一步) 往往是特征选择，这个过程的目的就是为了排除特征之间的共线性、选择相对较为独立的特征; .
• 对于分类任务来说，只要各类别的条件概率排序正确，无需精准概率值就可以得出正确分类;
• 如果属性间依赖对所有类别影响相同，或依赖关系的影响能相互抵消，则属性条件独立性假设在降低计算复杂度的同时不会对性能产生负面影响。

朴素贝叶斯与 LR 的区别？

简单来说：

区别一：

• 朴素贝叶斯是生成模型，

  • 根据已有样本进行贝叶斯估计学习出先验概率 P(Y) 和条件概率 P(X|Y),
  • 进而求出联合分布概率 P(XY),
  • 最后利用贝叶斯定理求解 P(Y|)X),

• 而 LR 是判别模型，

  • 根据极大化对数似然函数直接求出条件概率 P(Y|X);

• 从概率框架的角度来理解机器学习;主要有两种策略：

  第一种：给定 x，可通过直接建模 P(C |x) 来预测 C，这样得到的是"判别式模型" (discriminative models);

  第二种：也可先对联合概率分布 P(x,c) 建模，然后再由此获得 P(c |x)，这样 得到的是"生成式模型" (generative models) ;

  显然，前面介绍的逻辑回归、决策树、都可归入判别式模型的范畴，还有后面学到的 BP 神经网络支持向量机等; 对生成式模型来说，必然需要考虑

  $$P(c|x)=\frac{P(x,c)}{P(x)}$$

区别⼆：

• 朴素贝叶斯是基于很强的条件独立假设 (在已知分类 Y 的条件下，各个特征变量取值是相互独立的)，
• 而 LR 则对此没有要求;

区别三：

• 朴素贝叶斯适用于数据集少的情景，
• 而 LR 适用于大规模数据集。

进一步说明：

前者是生成式模型，后者是判别式模型，二者的区别就是生成式模型与判别式模型的区别。

• 首先，Navie Bayes 通过已知样本求得先验概率 P(Y),及条件概率 P(X|Y) ,对于给定的实例，计算联合概率，进而求出后验概率。也就是说，它尝试去找到底这个数据是怎么生成的 (产生的) ，然后再进行分类。哪个类别最有可能产生这个信号，就属于那个类别。

  • 优点：样本容量增加时，收敛更快;隐变量存在时也可适用。
  • 缺点：时间长;需要样本多;浪费计算资源

• 相比之下，Logistic 回归不关心样本中类别的比例及类别下出现特征的概率，它直接给出预测模型的式子。设每个特征都有一个权重，训练样本数据更新权重 w，得出最终表达式。

  • 优点：
    • 直接预测往往准确率更高;
    • 简化问题;
    • 可以反应数据的分布情况，类别的差异特征;
    • 适用于较多类别的识别。
  • 缺点
    • 收敛慢;
    • 不适用于有隐变量的情况。

贝叶斯原理是英国数学家托马斯·贝叶斯提出的。贝叶斯是个很神奇的人，他的经历类似梵高。生前没有得到重视，死后，他写的一篇关于归纳推理的论文被朋友翻了出来，并发表了。这一发表不要紧，结果这篇论文的思想直接影响了接下来两个多世纪的统计学，是科学史上著名的论文之一。

贝叶斯原理跟我们的生活联系非常紧密。举个例子，如果你看到一个人总是花钱，那么会推断这个人多半是个有钱人。当然这也不是绝对，也就是说，当你不能准确预知一个事物本质的时候，你可以依靠和事物本质相关的事件来进行判断，如果事情发生的频次多，则证明这个属性更有可能存在。

如何对文档进行分类

如果我们要对文档进行分类，有两个重要的阶段：

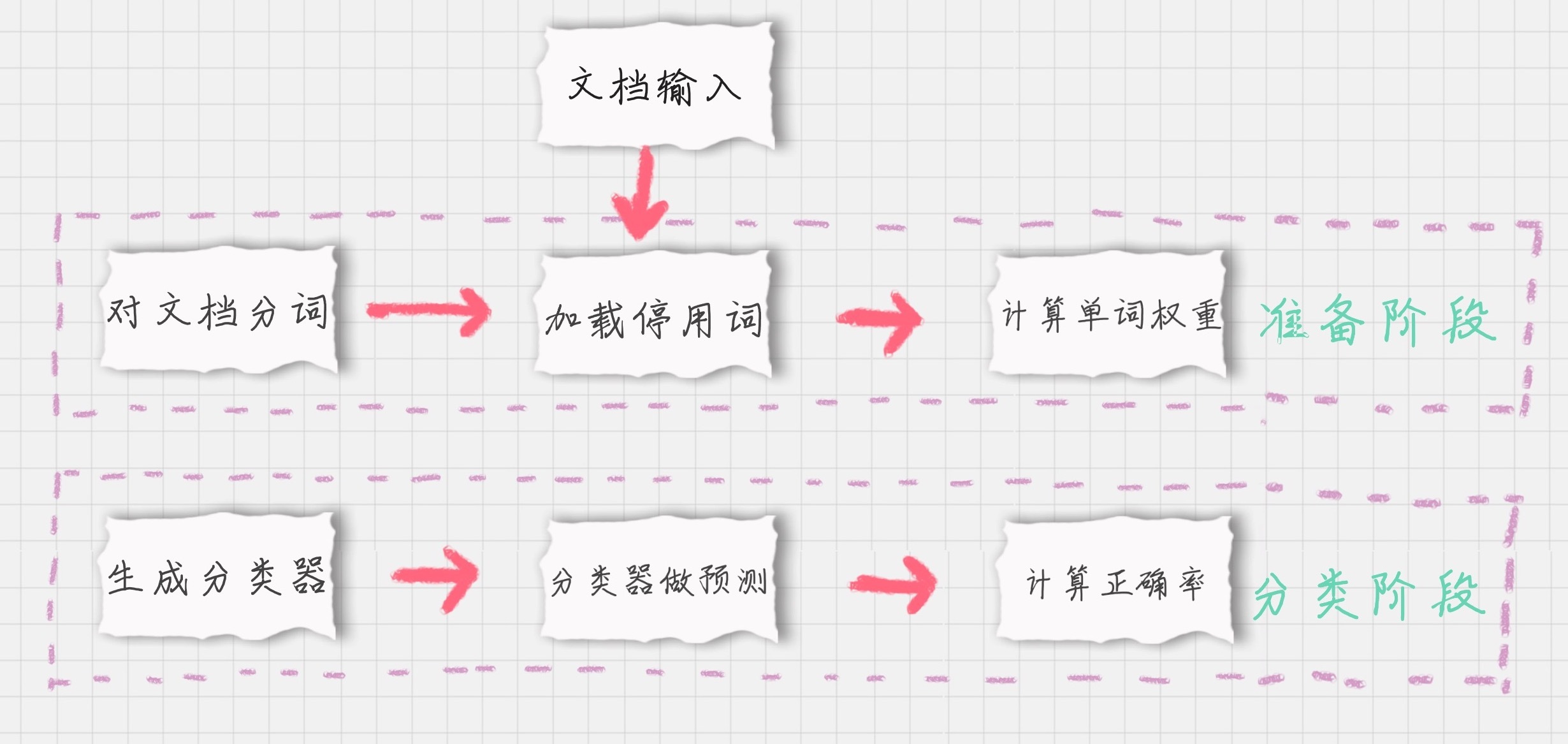
1. 基于分词的数据准备，包括分词、单词权重计算、去掉停用词；
2. 应用朴素贝叶斯分类进行分类，首先通过训练集得到朴素贝叶斯分类器，然后将分类器应用于测试集，并与实际结果做对比，最终得到测试集的分类准确率。

下面，我分别对这些模块进行介绍。

模块 1：对文档进行分词

在准备阶段里，最重要的就是分词。那么如果给文档进行分词呢？英文文档和中文文档所使用的分词工具不同。

在英文文档中，最常用的是 NTLK 包。NTLK 包中包含了英文的停用词 stop words、分词和标注方法。

import nltk

word_list = nltk.word_tokenize(text)  # 分词
nltk.pos_tag(word_list)  # 标注单词的词性

在中文文档中，最常用的是 jieba 包。jieba 包中包含了中文的停用词 stop words 和分词方法。

import jieba

word_list = jieba.cut(text)  # 中文分词

模块 2：加载停用词表

我们需要自己读取停用词表文件，从网上可以找到中文常用的停用词保存在 stop_words.txt，然后利用 Python 的文件读取函数读取文件，保存在 stop_words 数组中。

stop_words = [line.strip().decode('utf-8') for line in io.open('stop_words.txt').readlines()]

模块 3：计算单词的权重

这里我们用到 sklearn 里的 TfidfVectorizer 类，上面我们介绍过它使用的方法。

直接创建 TfidfVectorizer 类，然后使用 fit_transform 方法进行拟合，得到 TF-IDF 特征空间 features，你可以理解为选出来的分词就是特征。我们计算这些特征在文档上的特征向量，得到特征空间 features。

tf = TfidfVectorizer(stop_words=stop_words, max_df=0.5)
features = tf.fit_transform(train_contents)

这里 max_df 参数用来描述单词在文档中的最高出现率。假设 max_df=0.5，代表一个单词在 50% 的文档中都出现过了，那么它只携带了非常少的信息，因此就不作为分词统计。

一般很少设置 min_df，因为 min_df 通常都会很小。

模块 4：生成朴素贝叶斯分类器

我们将特征训练集的特征空间 train_features，以及训练集对应的分类 train_labels 传递给贝叶斯分类器 clf，它会自动生成一个符合特征空间和对应分类的分类器。

这里我们采用的是多项式贝叶斯分类器，其中 alpha 为平滑参数。为什么要使用平滑呢？因为如果一个单词在训练样本中没有出现，这个单词的概率就会被计算为 0。但训练集样本只是整体的抽样情况，我们不能因为一个事件没有观察到，就认为整个事件的概率为 0。为了解决这个问题，我们需要做平滑处理。

当 alpha=1 时，使用的是 Laplace 平滑。Laplace 平滑就是采用加 1 的方式，来统计没有出现过的单词的概率。这样当训练样本很大的时候，加 1 得到的概率变化可以忽略不计，也同时避免了零概率的问题。

当 0<alpha<1 时，使用的是 Lidstone 平滑。对于 Lidstone 平滑来说，alpha 越小，迭代次数越多，精度越高。我们可以设置 alpha 为 0.001。

# 多项式贝叶斯分类器
from sklearn.naive_bayes import MultinomialNB

clf = MultinomialNB(alpha=0.001).fit(train_features, train_labels)

模块 5：使用生成的分类器做预测

首先我们需要得到测试集的特征矩阵。

方法是用训练集的分词创建一个 TfidfVectorizer 类，使用同样的 stop_words 和 max_df，然后用这个 TfidfVectorizer 类对测试集的内容进行 fit_transform 拟合，得到测试集的特征矩阵 test_features。

test_tf = TfidfVectorizer(stop_words=stop_words, max_df=0.5, vocabulary=train_vocabulary)
test_features = test_tf.fit_transform(test_contents)

然后我们用训练好的分类器对新数据做预测。

方法是使用 predict 函数，传入测试集的特征矩阵 test_features，得到分类结果 predicted_labels。predict 函数做的工作就是求解所有后验概率并找出最大的那个。

predicted_labels = clf.predict(test_features)

模块 6：计算准确率

计算准确率实际上是对分类模型的评估。我们可以调用 sklearn 中的 metrics 包，在 metrics 中提供了 accuracy_score 函数，方便我们对实际结果和预测的结果做对比，给出模型的准确率。

使用方法如下：

from sklearn import metrics

print(metrics.accuracy_score(test_labels, predicted_labels))