逻辑回归介绍

逻辑回归（Logistic Regression）算法的名字里虽然带有“回归”二字，但实际上逻辑回归算法是用来解决分类问题的算法。由于算法的简单和高效，在实际中应用非常广泛。

就其模型本身而言，有以下几个特点。

模型简单：建模思路清晰，容易理解与掌握。
适用范围广：模型的假设容易被满足，适用的场景很多。
模型可解释性强：模型参数有对应的实际意义，而且参数的取值直接反映特征的强弱，具有强解释性。
结果可靠性强：与线性回归模型类似，有很好的数学工具对模型参数和模型结果做分析，比如稳定性分析等。这使得模型结果的可信度很高。

逻辑回归的原理

假设有一场足球赛，我们有两支球队的所有出场球员信息、历史交锋成绩、比赛时间、主客场、裁判和天气等信息，根据这些信息预测球队的输赢。假设比赛结果记为 y，赢球标记为 1，输球标记为 0，这个就是典型的二元分类问题，可以用逻辑回归算法来解决。

从这个例子里可以看出，逻辑回归算法的输出是个离散值，这是与线性回归算法的最大区别。

逻辑回归主要的应用场景为：

广告点击率
是否为垃圾邮件
是否患病
金融诈骗
虚假账号

看到上面的例子，我们可以发现其中的特点，那就是都属于两个类别之间的判断。逻辑回归就是解决二分类问题的利器

逻辑回归的数据输入

要想掌握逻辑回归，必须掌握两点：

逻辑回归中，其输入值是什么
如何判断逻辑回归的输出

h (w) = w_{1} x_{1} + w_{2} x_{2} + w_{3} x_{3} + b

逻辑回归的输入就是一个线性回归的结果。

然后将一个线性结果进行二分类

预测函数

需要找出一个预测函数模型，使其值输出在[0，1]之间。然后选择一个基准值，如 0.5，如果算出来的预测值大于 0.5，就认为其预测值为 1，反之则其预测值为 0。

g (z) = \frac{1}{1 + e^{- z_{1}}}

来作为预测函数，其中 e 是自然对数的底数。函数 g（z）称为 Sigmoid 函数，也称为 Logistic 函数。以 z 为横坐标，以 g（z）为纵坐标

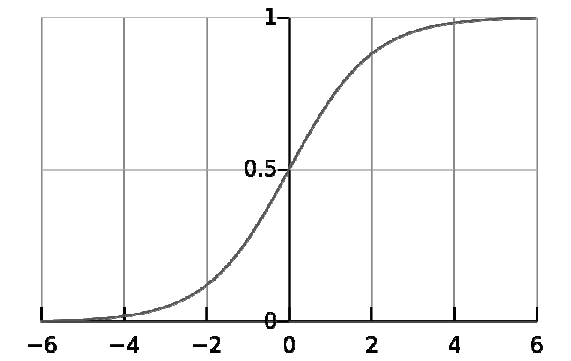
从图中可以看出，当 z=0 时，g（z）=0.5。当 z＞0 时，g（z）＞0.5，当 z 越来越大时，g（z）无限接近于 1。当 z＜0 时，g（z）＜0.5，当 z 越来越小时，g（z）无限接近于 0。这正是我们想要的针对二元分类算法的预测函数。

问题来了，怎样把输入特征和预测函数结合起来呢？

结合线性回归函数的预测函数 h~θ~（x）=θ^T^x，假设令 z（x）=θ^T^x，则逻辑回归算法的预测函数如下：

h_{θ} (x) = g (z) = g (θ^{T} x) = \frac{1}{1 + e^{- θ^{T} x}}

下面来解读预测函数。

h~θ~（x）表示在输入值为 x，参数为θ的前提条件下 y=1 的概率。用概率论的公式可以写成：

h_{θ} (x) = P (y = 1 | x, θ)

上面的概率公式可以读成：[在输入 x 及参数θ条件下 y=1 的概率]，这是个条件概率公式。由概率论的知识可以推导出

P (y = 1 | x, θ) + P (y = 0 | x, θ) = 1

对二元分类法来说，这是个非黑即白的世界。

判定边界

逻辑回归算法的预测函数由下面两个公式给出的：

h_{θ} = g (θ^{T} x)

假定 y=1 的判定条件是 h~θ~（x）≥0.5，y=0 的判定条件是 h~θ~（x）＜0.5，则可以推导出 y=1 的判定条件就是θ^T^x≥0，y=0 的判定条件就是θ^T^x＜0。所以，θ^T^x=0 即是我们的判定边界。

下面给出两个判定边界的例子。

假定有两个变量 x~1~，x~2~，其逻辑回归预测函数是 h~θ~（x）=g（θ~0~+θ~1~x~1~+θ~2~x~2~）。假设给定参数

θ = [\begin{matrix} - 3 \\ 1 \\ 1 \end{matrix}]

那么可以得到判定边界 -3+x~1~+x~2~=0，即 x~1~+x~2~=3，如果以 x~1~为横坐标，x~2~ 为纵坐标，则这个函数画出来就是一个通过（0，3）和（3，0）两个点的斜线。这条线就是判定边界，如图 6-2 左图所示。

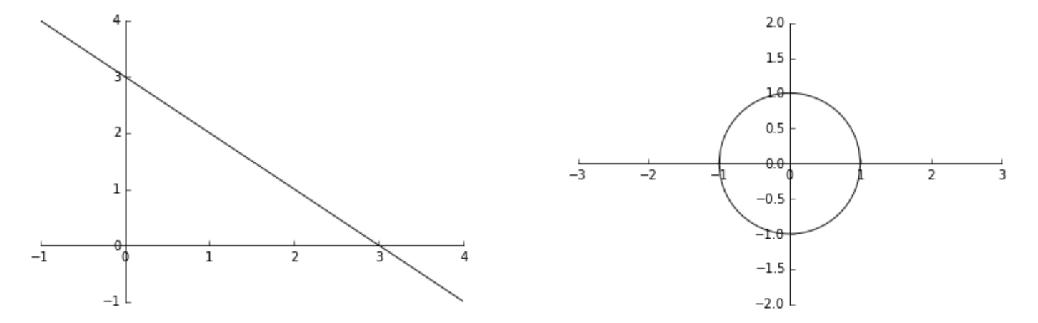
其中，直线左下角为 y=0，直线右上解为 y=1。横坐标为 x~1~，纵坐标为 x~2~。

如果预测函数是多项式

h_{θ} (x) = g (θ_{0} + θ_{1} x_{1} + θ_{2} x_{2} + θ_{3} x_{1}^{2} + θ_{3} x_{2}^{2})

且给定

θ = [\begin{matrix} - 1 \\ 0 \\ 0 \\ 1 \\ 1 \end{matrix}]

则可以得到判定边界函数 $x_{1}^{2} + x_{2}^{2} = 1$ 。

还是以 x~1~为横坐标，x~2~为纵坐标，则这是一个半径为 1 的圆。圆内部是 y=0，圆外部是 y=1，这是二阶多项式的情况，更一般的多阶多项式可以表达出更复杂的判定边界。

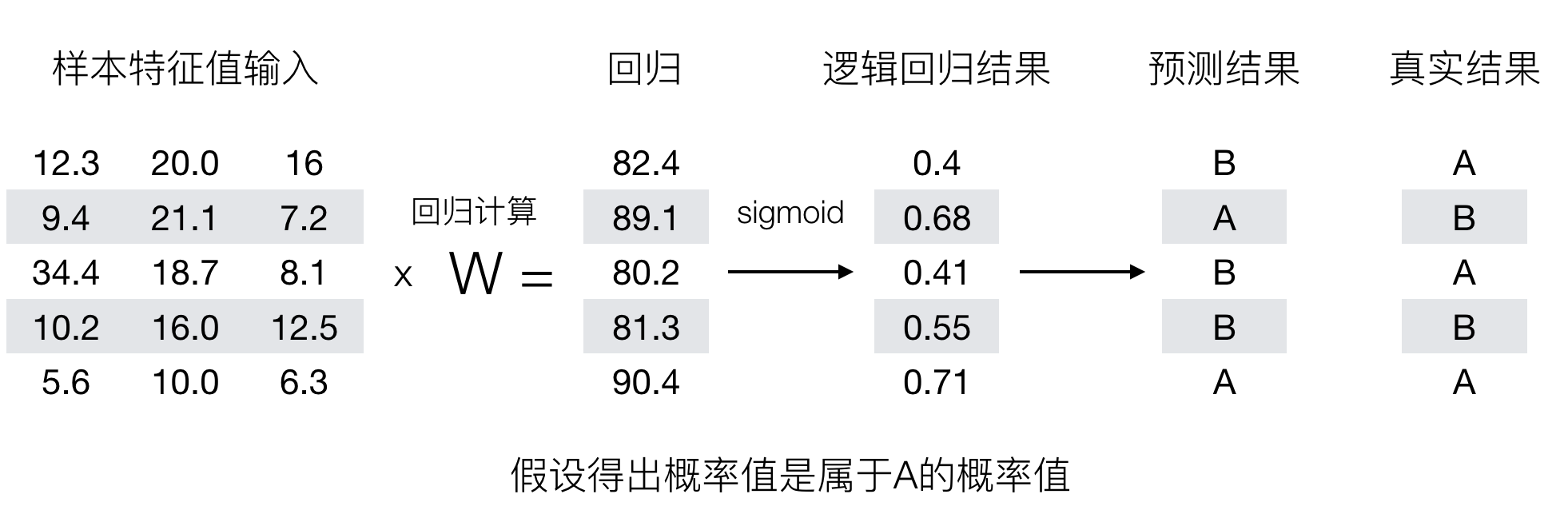
逻辑回归最终的分类是通过属于某个类别的概率值来判断是否属于某个类别，并且这个类别默认标记为 1(正例),另外的一个类别会标记为 0(反例)。（方便损失计算）

输出结果解释 (重要)：假设有两个类别 A，B，并且假设我们的概率值为属于 A(1) 这个类别的概率值。现在有一个样本的输入到逻辑回归输出结果 0.55，那么这个概率值超过 0.5，意味着我们训练或者预测的结果就是 A(1) 类别。那么反之，如果得出结果为 0.3 那么，训练或者预测结果就为 B(0) 类别。

关于逻辑回归的阈值是可以进行改变的，比如上面举例中，如果你把阈值设置为 0.6，那么输出的结果 0.55，就属于 B 类。

在之前，我们用最小二乘法衡量线性回归的损失

在逻辑回归中，当预测结果不对的时候，我们该怎么衡量其损失呢？

我们来看下图 (下图中，设置阈值为 0.6)，

é€"è¾‘å›žå½’è¿ç®—è¿‡ç¨‹

那么如何去衡量逻辑回归的预测结果与真实结果的差异呢？

损失以及优化

损失

逻辑回归的损失，称之为对数似然损失，公式如下：

分开类别：

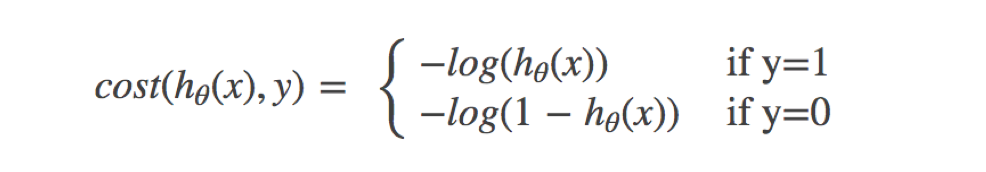
å•ä¸ªå¯¹æ•°ä¼¼ç„¶æŸå¤±

其中 y 为真实值，h~θ~(x) 为预测值

怎么理解单个的式子呢？这个要根据 log 的函数图像来理解

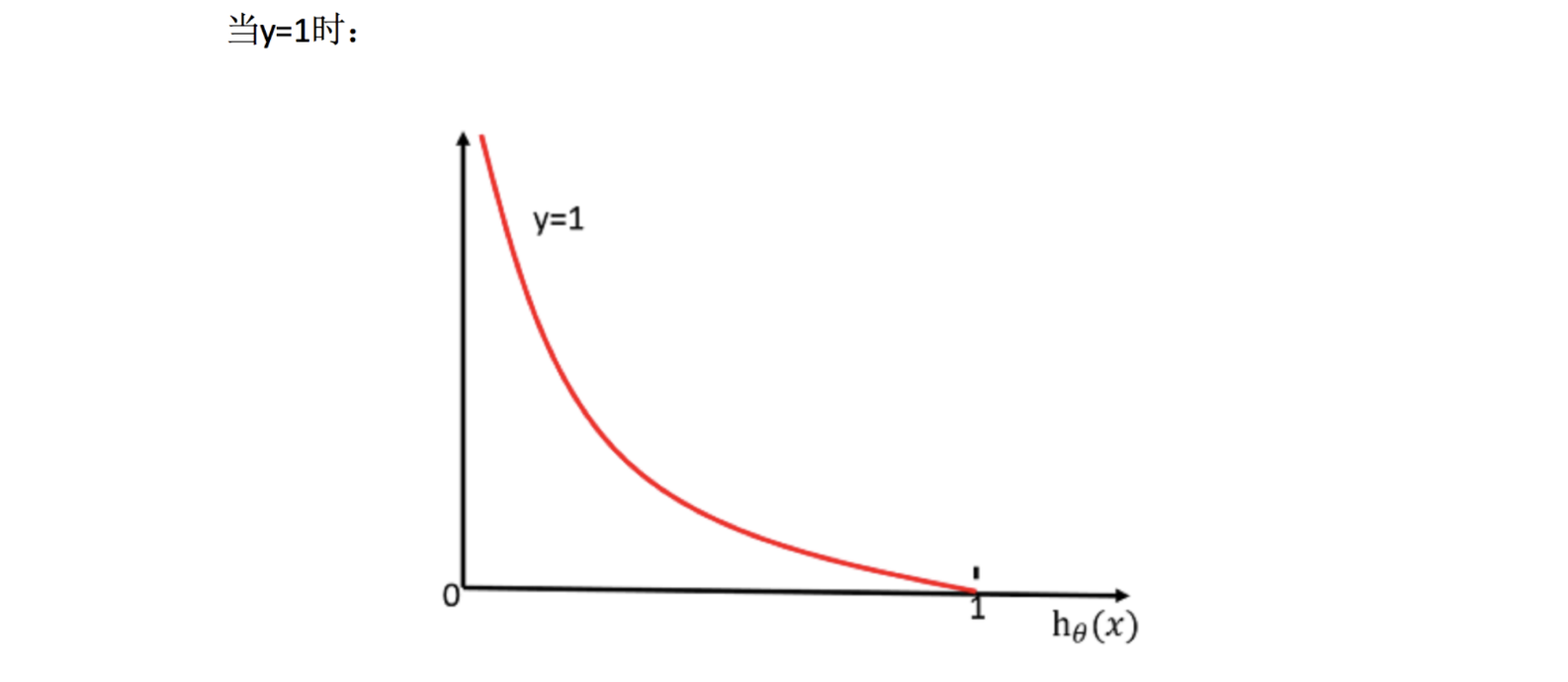
无论何时，我们都希望损失函数值，越小越好

分情况讨论，对应的损失函数值：

当 y=1 时，我们希望 $h_{θ} (x)$ 值越大越好；
当 y=0 时，我们希望 $h_{θ} (x)$ 值越小越好
综合完整损失函数

å®Œæ•´å¯¹æ•°ä¼¼ç„¶æŸå¤±

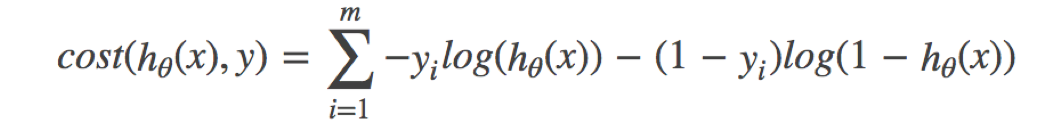
接下来我们呢就带入上面那个例子来计算一遍，就能理解意义了。

æŸå¤±è®¡ç®—è¿‡ç¨‹

我们已经知道，log(P), P 值越大，结果越小，所以我们可以对着这个损失的式子去分析

优化

同样使用梯度下降优化算法，去减少损失函数的值。这样去更新逻辑回归前面对应算法的权重参数，提升原本属于 1 类别的概率，降低原本是 0 类别的概率。

小结

逻辑回归概念【知道】
- 解决的是一个二分类问题
- 逻辑回归的输入是线性回归的输出
逻辑回归的原理【掌握】
- 输入：
  - 线性回归的输出
- 激活函数
  - sigmoid 函数
  - 把整体的值映射到 [0,1]
  - 再设置一个阈值，进行分类判断
逻辑回归的损失和优化【掌握】
- 损失
  - 对数似然损失
  - 借助了 log 思想，进行完成
  - 真实值等于 0，等于 1 两种情况进行划分
- 优化
  - 提升原本属于 1 类别的概率，降低原本是 0 类别的概率。

逻辑回归 api 介绍

python

sklearn.linear_model.LogisticRegression(solver='liblinear', penalty='l2', C=1.0)

solver 可选参数:{'liblinear', 'sag', 'saga','newton-cg', 'lbfgs'}，
- 默认：'liblinear'；用于优化问题的算法。
- 对于小数据集来说，“liblinear”是个不错的选择，而“sag”和'saga'对于大型数据集会更快。
- 对于多类问题，只有'newton-cg'， 'sag'， 'saga'和'lbfgs'可以处理多项损失;“liblinear”仅限于“one-versus-rest”分类。
penalty：正则化的种类
C：正则化力度

默认将类别数量少的当做正例

LogisticRegression 方法相当于 SGDClassifier(loss="log", penalty=" "),SGDClassifier 实现了一个普通的随机梯度下降学习。而使用 LogisticRegression(实现了 SAG)

逻辑回归介绍 ​

逻辑回归的原理 ​

逻辑回归的数据输入 ​

预测函数 ​

判定边界 ​

损失以及优化 ​

损失 ​

优化 ​

逻辑回归 api 介绍 ​