kd 树(原理、了解)
问题导入:
实现 k 近邻算法时,主要考虑的问题是如何对训练数据进行快速 k 近邻搜索。
这在特征空间的维数大及训练数据容量大时尤其必要。
k 近邻法最简单的实现是线性扫描(穷举搜索),即要计算输入实例与每一个训练实例的距离。计算并存储好以后,再查找 K 近邻。 当训练集很大时,计算非常耗时。
为了提高 kNN 搜索的效率,可以考虑使用特殊的结构存储训练数据,以减小计算距离的次数。
kd 树简介
什么是 kd 树
根据KNN每次需要预测一个点时,我们都需要计算训练数据集里每个点到这个点的距离,然后选出距离最近的 k 个点进行投票。 当数据集很大时,这个计算成本非常高。
kd 树:为了避免每次都重新计算一遍距离,算法会把距离信息保存在一棵树里,这样在计算之前从树里查询距离信息,尽量避免重新计算。其基本原理是, 如果 A 和 B 距离很远,B 和 C 距离很近,那么 A 和 C 的距离也很远。有了这个信息,就可以在合适的时候跳过距离远的点。
这样优化后的算法复杂度可降低到O(DNlog(N))。感兴趣的读者可参阅论文:Bentley,J.L.,Communications of the ACM(1975)。
1989 年,另外一种称为Ball Tree的算法,在 kd Tree 的基础上对性能进一步进行了优化。 感兴趣的读者可以搜索Five balltree construction algorithms来了解详细的算法信息。
原理
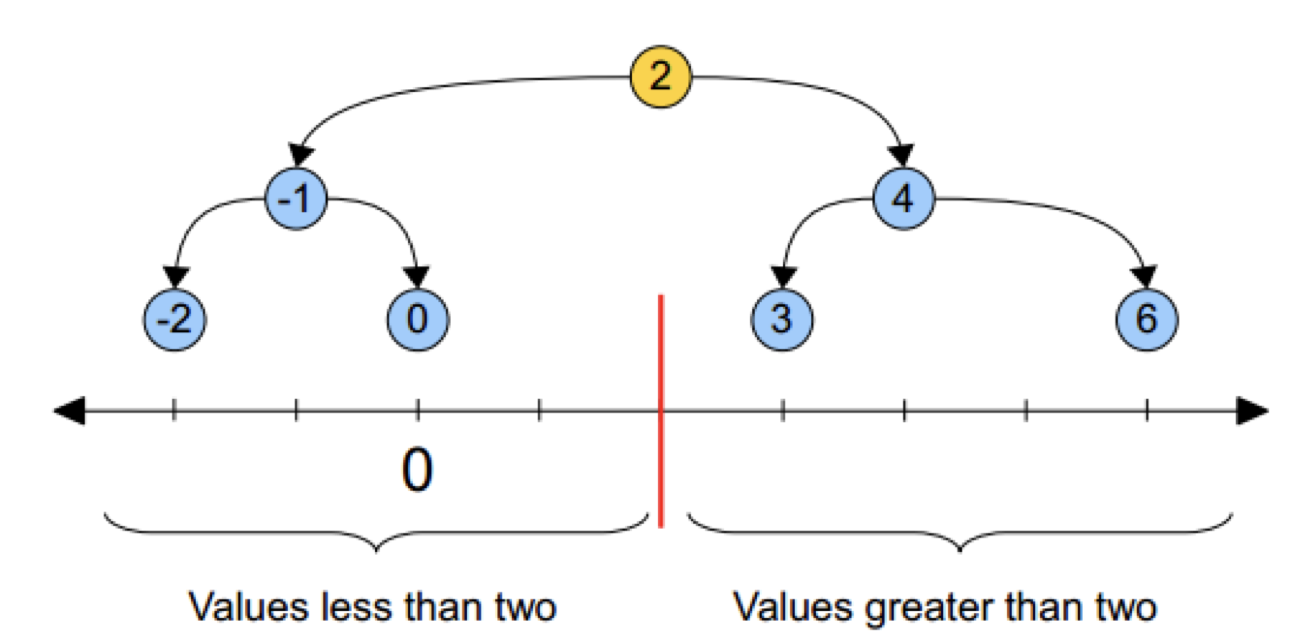
黄色的点作为根节点,上面的点归左子树,下面的点归右子树,接下来再不断地划分,分割的那条线叫做分割超平面(splitting hyperplane),在一维中是一个点,二维中是线,三维的是面。
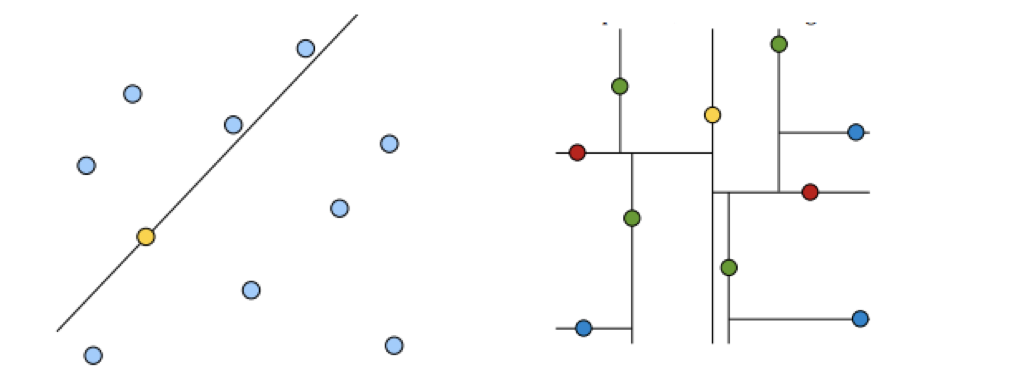
黄色节点就是 Root 节点,下一层是红色,再下一层是绿色,再下一层是蓝色。
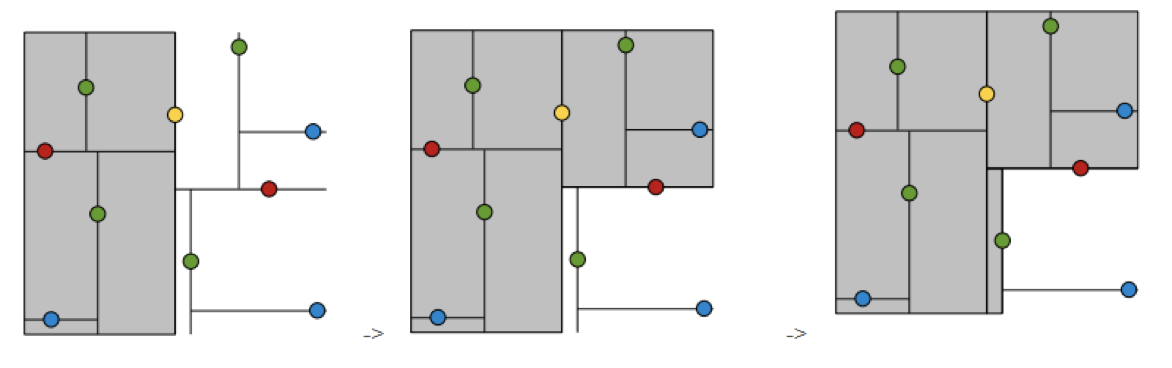
1. 树的建立;
2. 最近邻域搜索(Nearest-Neighbor Lookup)
kd 树 (K-dimension tree) 是一种对 k 维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。 kd 树是一种二叉树,表示对 k 维空间的一个划分, 构造 kd 树相当于不断地用垂直于坐标轴的超平面将 K 维空间切分,构成一系列的 K 维超矩形区域。kd 树的每个结点对应于一个 k 维超矩形区域。 利用 kd 树可以省去对大部分数据点的搜索,从而减少搜索的计算量。
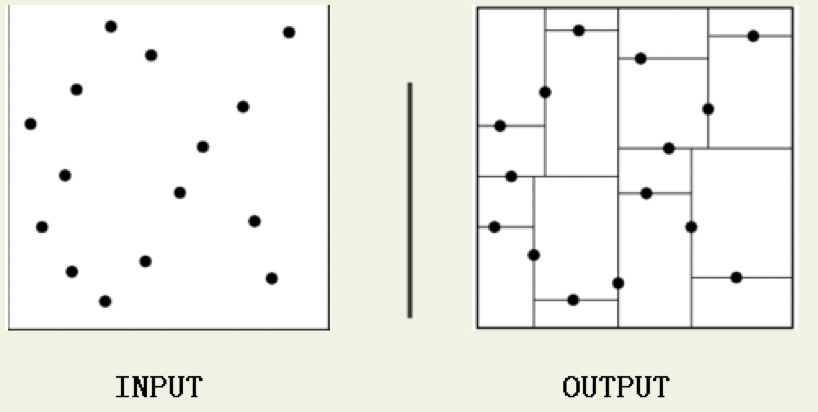
类比“二分查找”:给出一组数据:[9 1 4 7 2 5 0 3 8] ,要查找 8。如果挨个查找(线性扫描),那么将会把数据集都遍历一遍。而如果排一下序那数据集就变成了:[0 1 2 3 4 5 6 7 8 9] ,按前一种方式我们进行了很多没有必要的查找,现在如果我们以 5 为分界点,那么数据集就被划分为了左右两个“簇” [0 1 2 3 4] 和[6 7 8 9]。
因此,根本就没有必要进入第一个簇,可以直接进入第二个簇进行查找。把二分查找中的数据点换成 k 维数据点,这样的划分就变成了用超平面对 k 维空间的划分。空间划分就是对数据点进行分类,“挨得近”的数据点就在一个空间里面。
构造方法
(1)构造根结点,使根结点对应于 K 维空间中包含所有实例点的超矩形区域;
(2)通过递归的方法,不断地对 k 维空间进行切分,生成子结点。 在超矩形区域上选择一个坐标轴和在此坐标轴上的一个切分点,确定一个超平面,这个超平面通过选定的切分点并垂直于选定的坐标轴,将当前超矩形区域切分为左右两个子区域(子结点);这时,实例被分到两个子区域。
(3)上述过程直到子区域内没有实例时终止(终止时的结点为叶结点)。在此过程中,将实例保存在相应的结点上。
(4)通常,循环的选择坐标轴对空间切分,选择训练实例点在坐标轴上的中位数为切分点,这样得到的 kd 树是平衡的(平衡二叉树:它是一棵空树,或其左子树和右子树的深度之差的绝对值不超过 1,且它的左子树和右子树都是平衡二叉树)。
KD 树中每个节点是一个向量,和二叉树按照数的大小划分不同的是,KD 树每层需要选定向量中的某一维,然后根据这一维按左小右大的方式划分数据。在构建 KD 树时,关键需要解决 2 个问题:
(1)选择向量的哪一维进行划分;
(2)如何划分数据;
第一个问题简单的解决方法可以是随机选择某一维或按顺序选择,但是**更好的方法应该是在数据比较分散的那一维进行划分(分散的程度可以根据方差来衡量) **。
第二个问题中,好的划分方法可以使构建的树比较平衡,可以每次选择中位数来进行划分。
案例分析
树的建立
给定一个二维空间数据集:T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)},构造一个平衡 kd 树。
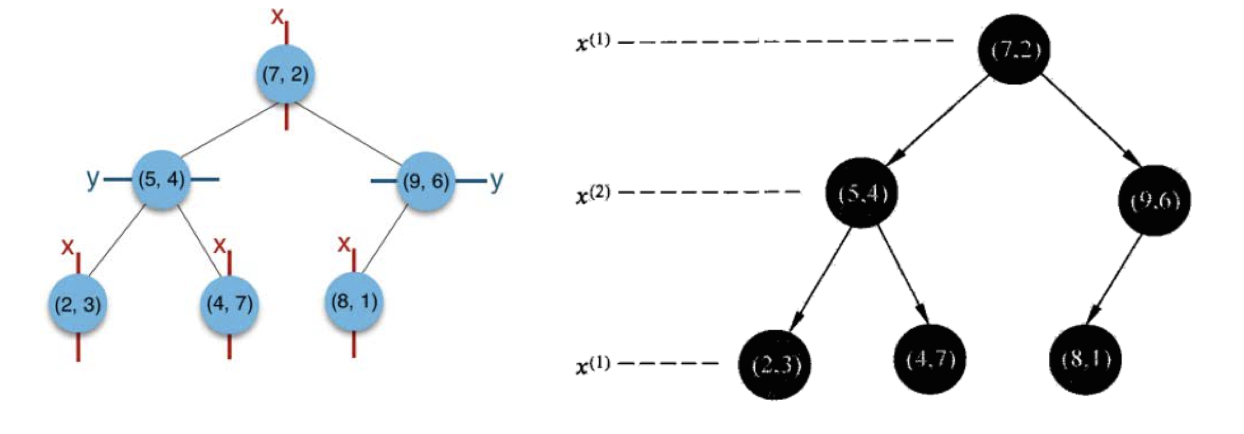
(1)思路引导:
根结点对应包含数据集 T 的矩形,选择 x(1) 轴,6 个数据点的 x(1) 坐标中位数是 6,这里选最接近的 (7,2) 点,以平面 x(1) =7 将空间分为左、右两个子矩形(子结点);接着左矩形以 x(2)=4 分为两个子矩形(左矩形中{(2,3),(5,4),(4,7)}点的 x(2) 坐标中位数正好为 4),右矩形以 x(2)=6 分为两个子矩形,如此递归,最后得到如下图所示的特征空间划分和 kd 树。
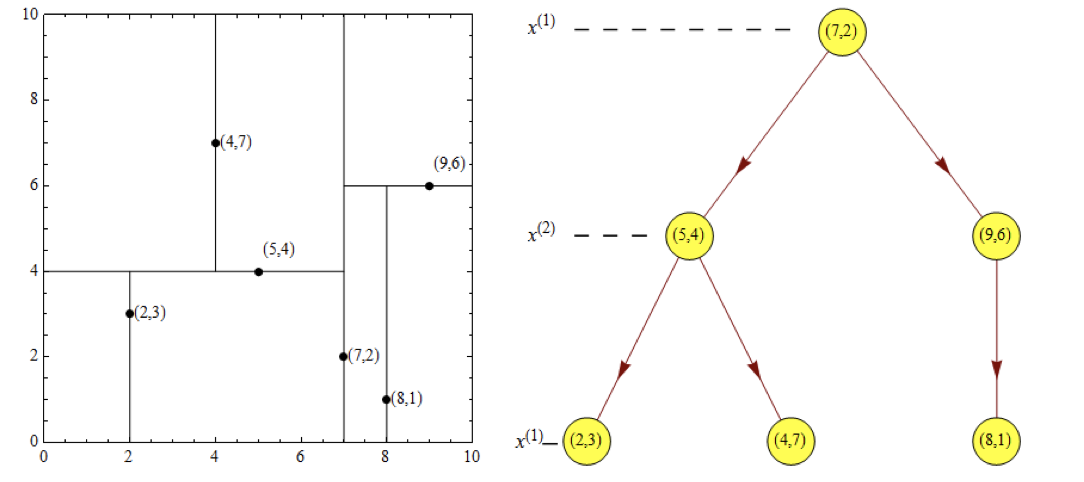
最近领域的搜索
假设标记为星星的点是 test point, 绿色的点是找到的近似点,在回溯过程中,需要用到一个队列,存储需要回溯的点,在判断其他子节点空间中是否有可能有距离查询点更近的数据点时, 做法是以查询点为圆心,以当前的最近距离为半径画圆,这个圆称为候选超球(candidate hypersphere),如果圆与回溯点的轴相交,则需要将轴另一边的节点都放到回溯队列里面来。
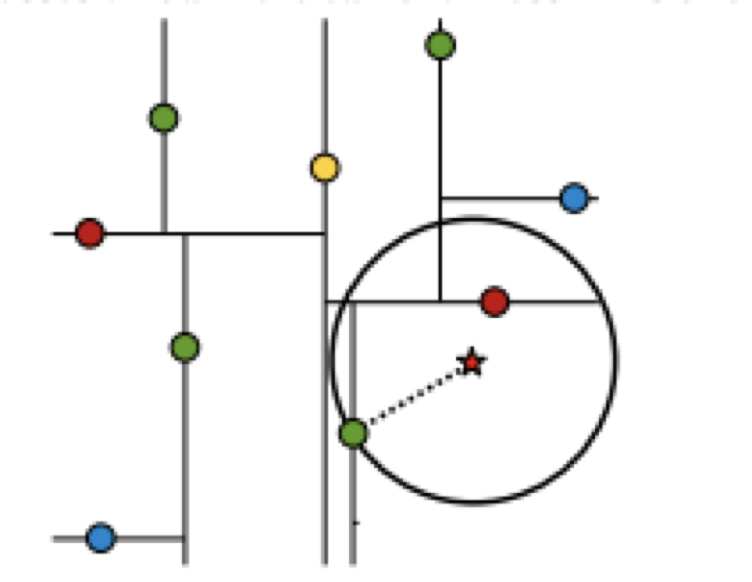
样本集{(2,3),(5,4), (9,6), (4,7), (8,1), (7,2)}
查找点 (2.1,3.1)
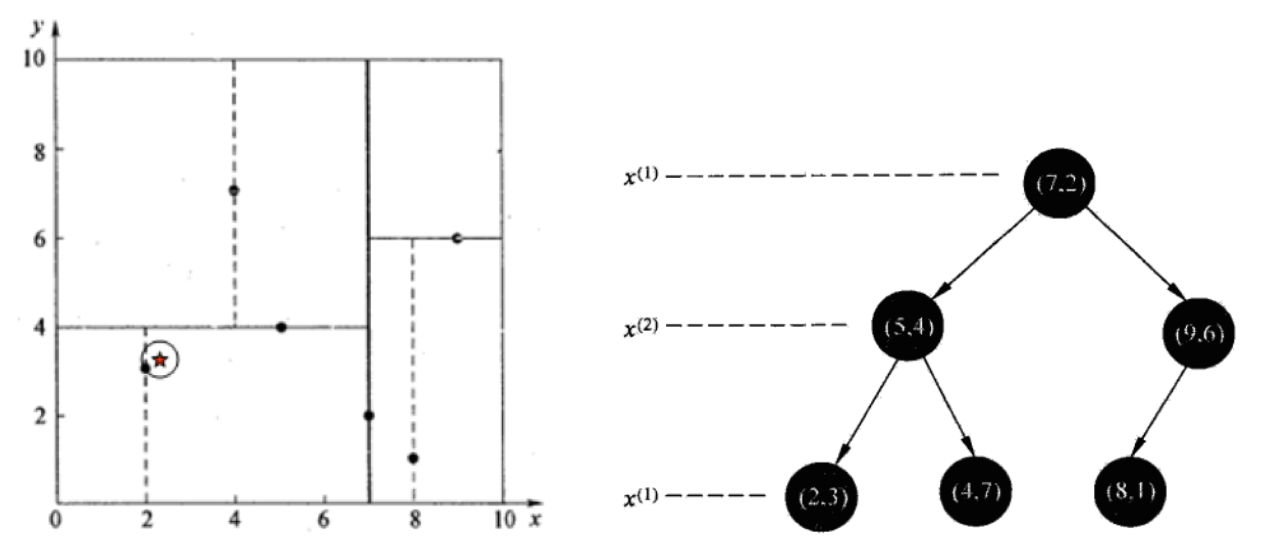
在 (7,2) 点测试到达 (5,4),在 (5,4) 点测试到达 (2,3),然后 search_path 中的结点为<(7,2),(5,4), (2,3)>,从 search_path 中取出 ( 2,3) 作为当前最佳结点 nearest, dist 为 0.141;
然后回溯至 (5,4),以 (2.1,3.1) 为圆心,以 dist=0.141 为半径画一个圆,并不和超平面 y=4 相交,如上图,所以不必跳到结点 (5,4) 的右子空间去搜索,因为右子空间中不可能有更近样本点了。
于是再回溯至 (7,2),同理,以 (2.1,3.1) 为圆心,以 dist=0.141 为半径画一个圆并不和超平面 x=7 相交,所以也不用跳到结点 (7,2) 的右子空间去搜索。
至此,search_path 为空,结束整个搜索,返回 nearest(2,3)作为(2.1,3.1)的最近邻点,最近距离为 0.141。
查找点 (2,4.5)
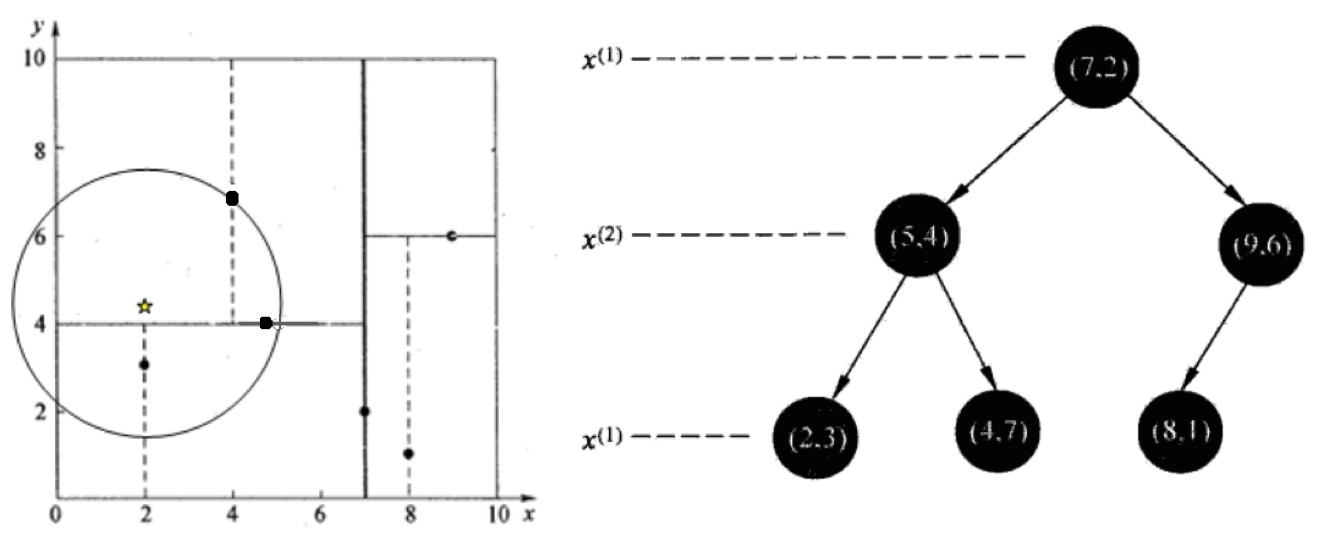
在 (7,2) 处测试到达 (5,4),在 (5,4) 处测试到达 (4,7)【优先选择在本域搜索】,然后 search_path 中的结点为<(7,2),(5,4), (4,7)> ,从 search_path 中取出 (4,7) 作为当前最佳结点 nearest, dist 为 3.202;
然后回溯至 (5,4),以 (2,4.5) 为圆心,以 dist=3.202 为半径画一个圆与超平面 y=4 相交,所以需要跳到 (5,4) 的左子空间去搜索。所以要将 (2,3) 加入到 search_path 中,现在 search_path 中的结点为<(7,2),(2, 3)>; 另外,(5,4) 与 (2,4.5) 的距离为 3.04 < dist = 3.202,所以将 (5,4) 赋给 nearest,并且 dist=3.04。
回溯至 (2,3),(2,3) 是叶子节点,直接平判断 (2,3) 是否离 (2,4.5) 更近,计算得到距离为 1.5,所以 nearest 更新为 (2,3),dist 更新为 (1.5)
回溯至 (7,2),同理,以 (2,4.5) 为圆心,以 dist=1.5 为半径画一个圆并不和超平面 x=7 相交,所以不用跳到结点 (7,2) 的右子空间去搜索。
至此,search_path 为空,结束整个搜索,返回 nearest(2,3) 作为 (2,4.5) 的最近邻点,最近距离为 1.5。