神经网络基础

神经网络
分类的损失函数
网络优化方法
案例 - 价格分类案例
Transformer 模型

神经网络

人工神经网络（Artificial Neural Network，简写为 ANN）也简称为神经网络（NN），是一种模仿生物神经网络结构和功能的计算模型。人脑可以看做是一个生物神经网络，由众多的神经元连接而成。各个神经元传递复杂的电信号，树突接收到输入信号，然后对信号进行处理，通过轴突输出信号。下图是生物神经元示意图：

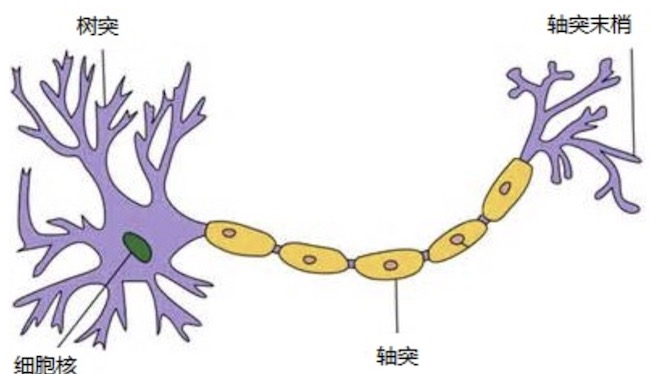
当电信号通过树突进入到细胞核时，会逐渐聚集电荷。达到一定的电位后，细胞就会被激活，通过轴突发出电信号。

那怎么构建人工神经网络中的神经元呢？

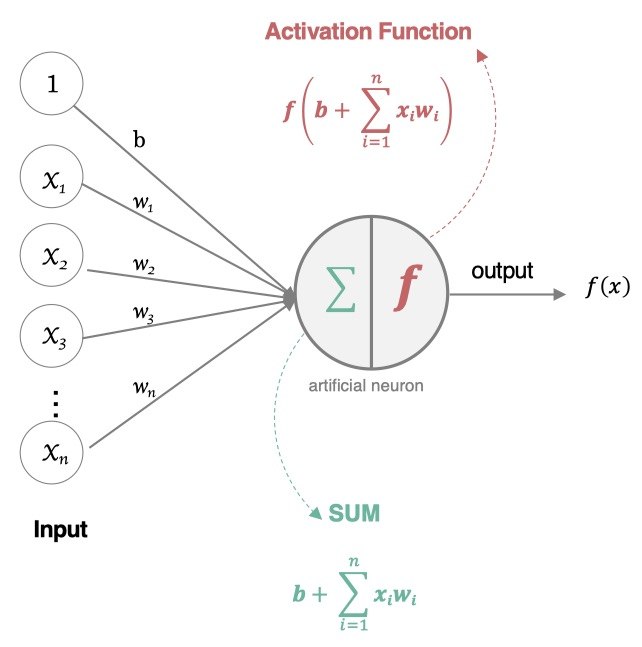
这个过程就像，来源不同树突 (树突都会有不同的权重) 的信息，进

行的加权计算，输入到细胞中做加和，再通过激活函数输出细胞值。

接下来，我们使用多个神经元来构建神经网络，相邻层之间的神经元相互连接，并给每一个连接分配一个强度，如下图所示：

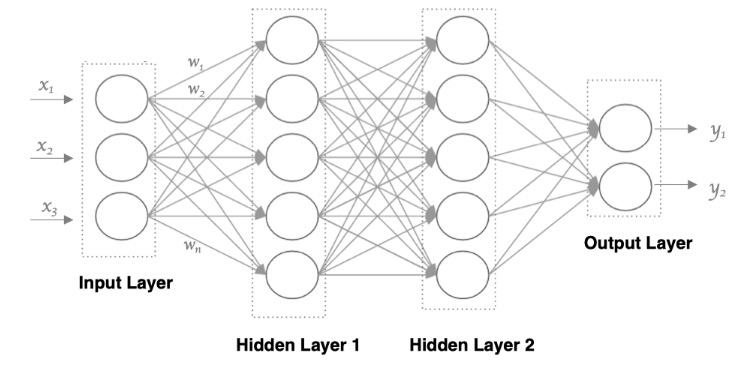
神经网络中信息只向一个方向移动，即从输入节点向前移动，通过隐藏节点，再向输出节点移动。其中的基本部分是：

1. 输入层: 即输入 x 的那一层

2. 输出层: 即输出 y 的那一层

3. 隐藏层: 输入层和输出层之间都是隐藏层

特点是：

同一层的神经元之间没有连接。
第 N 层的每个神经元和第 N-1 层的所有神经元相连（这就是 full connected 的含义)，这就是全连接神经网络。
第 N-1 层神经元的输出就是第 N 层神经元的输入。
每个连接都有一个权重值（w 系数和 b 系数）。

总结

1、知道深度学习与机器学习的关系

深度学习是机器学习的⼀个⼦集，主要区别在是否包含特征⼯程

2、知道神经⽹络是什么

⼀种模仿⽣物神经⽹络结构和功能的计算模型，由神经元构成（加权和 + 激活函数）

3、神经网络的构成

输入层，隐藏层和输出层

激活函数

激活函数用于对每层的输出数据进行变换, 进而为整个网络注入了非线性因素。此时，神经网络就

可以拟合各种曲线。

没有引入非线性因素的网络等价于使用一个线性模型来拟合
通过给网络输出增加激活函数，实现引入非线性因素，使得网络模型可以逼近任意函数，提升网络对复杂问题的拟合能力。

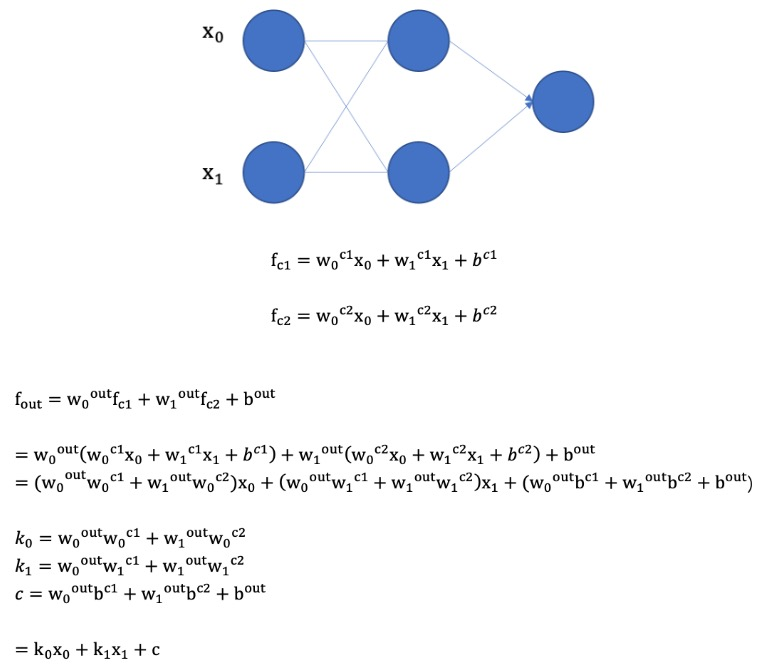
如果不使用激活函数，整个网络虽然看起来复杂，其本质还相当于一种线性模型，如下公式所示：

sigmoid 激活函数

激活函数公式： $f (x) = \frac{1}{1 + e^{- x}}$

激活函数求导公式： $f^{'} (x) = {(\frac{1}{1 + e^{- x}})}^{'} = \frac{1}{1 + e^{- x}} (1 - \frac{1}{1 + e^{- x}}) = f (x) (1 - f (x))$

sigmoid 激活函数的函数图像如下：

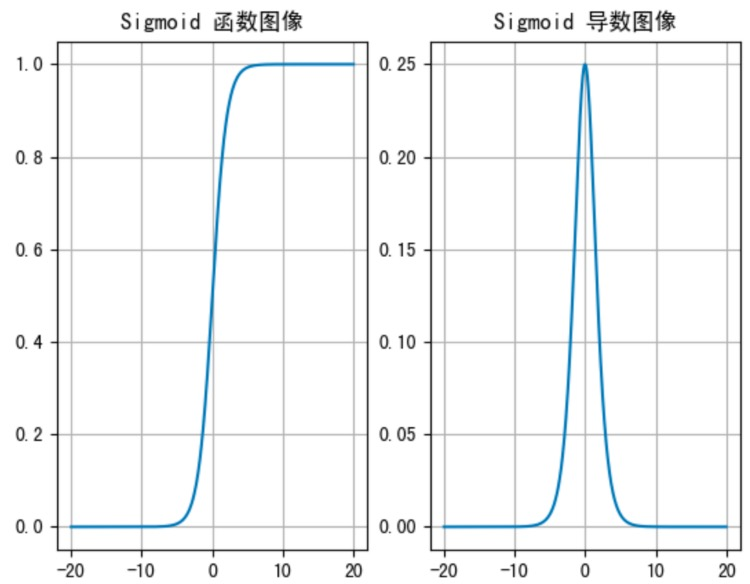
sigmoid 函数可以将任意的输入映射到 (0, 1) 之间，当输入的值大致在 <-6 或者 >6 时，意味着输入任何值得到的激活值都是差不多的，这样会丢失部分的信息。比如：输入 100 和输出 10000 经过 sigmoid 的激活值几乎都是等于 1 的，但是输入的数据之间相差 100 倍的信息就丢失了。
对于 sigmoid 函数而言，输入值在 [-6, 6] 之间输出值才会有明显差异，输入值在 [-3, 3] 之间才会**有比较好的效果 **。
通过上述导数图像，我们发现导数数值范围是 (0, 0.25)，当输入 <-6 或者 >6 时，sigmoid 激活函数图像的导数接近为 0，此时 网络参数将更新极其缓慢，或者无法更新。
一般来说，sigmoid 网络在 5 层之内就会产生梯度消失现象。而且，该激活函数并不是以 0 为中心的，所以在实践中这种激活函数使用的很少。 sigmoid 函数一般只用于二分类的输出层。

ReLU 激活函数

ReLU 公式如下： $f (x) = max (0, x)$
激活函数求导公式： $f^{'} (x) = 0 or 1$
ReLU 的函数图像如下：

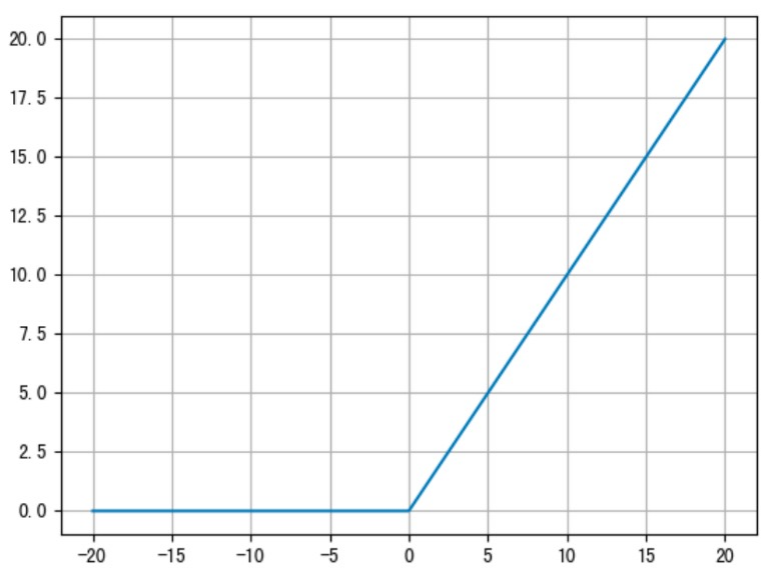
ReLU 激活函数将小于 0 的值映射为 0，而大于 0 的值则保持不变，它更加重视正信号，而忽略负信号，这种激活函数运算更为简单，能够提高模型的训练效率。
当 x<0 时，ReLU 导数为 0，而当 x>0 时，则不存在饱和问题。所以，ReLU 能够在 x> 0 时保持梯度不衰减，从而缓解梯度消失问题。然而，随着训练的推进，部分输入会落入小于 0 区域，导致对应权重无法更新。这种现象被称为“神经元死亡” 。
ReLU 是目前最常用的激活函数。与 sigmoid 相比，RELU 的优势是：采用 sigmoid 函数，计算量大（指数运算），反向传播求误差梯度时，计算量相对大，而采用 Relu 激活函数，整个过程的计算量节省很多。 sigmoid 函数反向传播时，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练。Relu 会使一部分神经元的输出为 0，这样就造成了网络的稀疏性，并且减少了参数的相互依存关系，缓解了过拟合问题的发生。

SoftMax 激活函数

softmax 用于多分类过程中，它是二分类函数 sigmoid 在多分类上的推广，目的是将多分类的结果以概率

的形式展现出来。计算方法如下图所示：

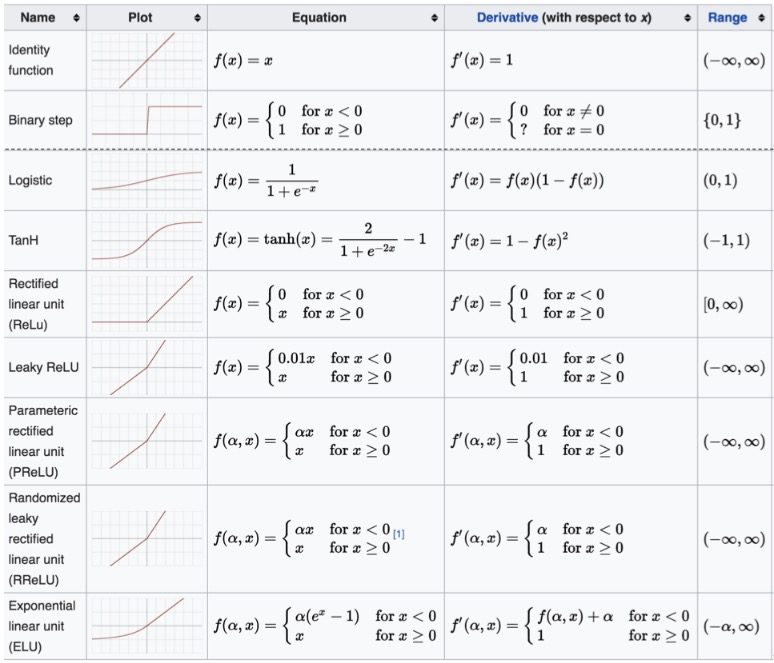
其他常见的激活函数

激活函数的选择方法

对于隐藏层:

优先选择 ReLU 激活函数
如果 ReLu 效果不好，那么尝试其他激活，如 Leaky ReLu 等。
如果你使用了 ReLU，需要注意一下 Dead ReLU 问题，避免出现大的梯度从而导致过多的神经元死亡。

对于输出层:

二分类问题选择 sigmoid 激活函数
多分类问题选择 softmax 激活函数

总结

激活函数的作用？
向神经网络中添加非线性元素
常见的激活函数及其特点？
Sigmoid, relu,softmax 等
激活函数的选择方法？
隐藏层：relu
输出层：二分类：sigmoid，多分类：softmax

神经网络搭建和参数计算

在 pytorch 中定义深度神经网络其实就是层堆叠的过程，继承自 nn.Module，实现两个方法：

__init__ 方法中定义网络中的层结构，主要是全连接层
forward 方法，在实例化模型的时候，底层会自动调用该函数。该函数中可以定义数据的传播方式，为

初始化定义的 layer 传入数据等。

我们来构建如下图所示的神经网络模型：

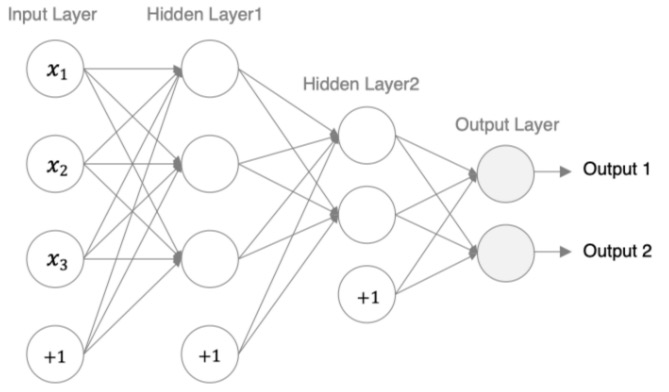
编码设计如下：

第 1 个隐藏层：激活函数使用 sigmoid
第 2 个隐藏层：激活函数采用 relu
out 输出层线性层假若多分类任务，采用 softmax 做激活

python

import torch
import torch.nn as nn
from torchsummary import summary  # 计算模型参数，查看模型结构，pip install torchsummary


## 创建神经网络模型类
class Model(nn.Module):
    # 初始化属性值
    def __init__(self):
        super(Model, self).__init__()  # 调用父类的初始化属性值
        self.linear1 = nn.Linear(3, 3)  # 创建第一个隐藏层模型，3 个输入特征，3 个输出特征
        # 创建第二个隐藏层模型，3 个输入特征 (上一层的输出特征),2 个输出特征
        self.linear2 = nn.Linear(3, 2)
        # 创建输出层模型
        self.out = nn.Linear(2, 2)

    # 创建前向传播方法，自动执行 forward() 方法
    def forward(self, x):
        # 数据经过第一个线性层
        x = self.linear1(x)
        # 使用 sigmoid 激活函数
        x = torch.sigmoid(x)
        # 数据经过第二个线性层
        x = self.linear2(x)
        # 使用 relu 激活函数
        x = torch.relu(x)
        # 数据经过输出层
        x = self.out(x)
        # 使用 softmax 激活函数
        # dim=-1 维度数据相加为 1
        x = torch.softmax(x, dim=-1)
        return x


if __name__ == "__main__":
    # 实例化 model 对象
    my_model = Model()
    # 随机产生数据
    my_data = torch.randn(5, 3)
    print("mydata shape", my_data.shape)
    # 数据经过神经网络模型训练
    output = my_model(my_data)
    print("output shape-->", output.shape)
    # 计算模型参数
    # 计算每层每个神经元的 w 和 b 个数总和
    summary(my_model, input_size=(3,), batch_size=5)

输出结果：

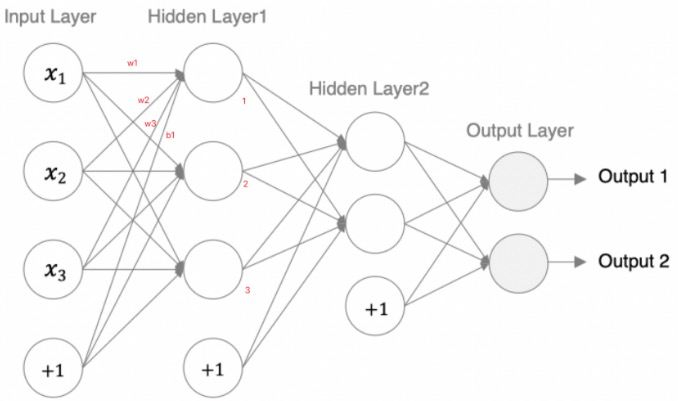
模型参数的计算：

以第一个隐层为例：该隐层有 3 个神经元，每个神经元的参数为：4 个（w1,w2,w3,b1），所以一共用 3x4=12 个参数。
输入数据和网络权重是两个不同的事儿！对于初学者理解这一点十分重要，要分得清。

总结

神经网络的搭建方法
- 定义继承自 nn.Module 的模型类
- 在__init__方法中定义网络中的层结构
- 在 forward 方法中定义数据传输方式
网络参数量的统计方法
- 统计每一层中的权重 w 和偏置 b 的数量

神经网络的优缺点

优点
- 精度⾼，性能优于其他的机器学习⽅法，甚⾄在某些领域超过了⼈类
- 可以近似任意的⾮线性函数
- 随之计算机硬件的发展，在学界和业界受到了热捧，有⼤量的框架和库可供调。
缺点
- ⿊箱，很难解释模型是怎么⼯作的
- 训练时间⻓，需要⼤量的计算⼒
- ⽹络结构复杂，需要调整超参数
- ⼩数据集上表现不佳，容易发⽣过拟合

损失函数

知道分类任务的损失函数

什么是损失函数

在深度学习中，损失函数是用来衡量模型参数的质量的函数，衡量的方式是比较网络输出和真实输出的差异：

多分类损失函数

在多分类任务通常使用 softmax 将 logits 转换为概率的形式，所以多分类的交叉熵损失也叫做 softmax 损失，它的计算方法是：

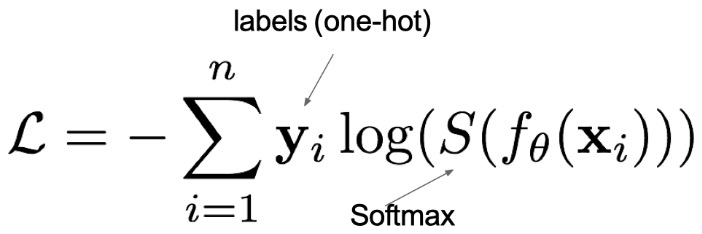
其中：

y 是样本 x 属于某一个类别的真实概率
而 f(x) 是样本属于某一类别的预测分数
S 是 softmax 激活函数，将属于某一类别的预测分数转换成概率
L 用来衡量真实值 y 和预测值 f(x) 之间差异性的损失结果

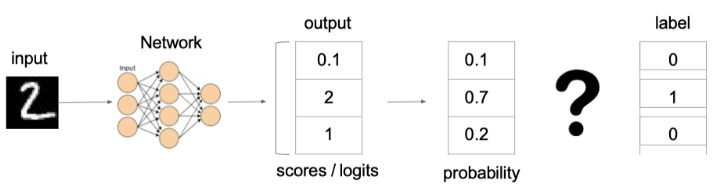
上图中的交叉熵损失为： $- (0 \log (0.10) + 1 \log (0.7) + 0 \log (0.2)) = - \log (0.7)$

从概率角度理解，我们的目的是最小化正确类别所对应的预测概率的对数的负值 (损失值最小)，如下图所示：

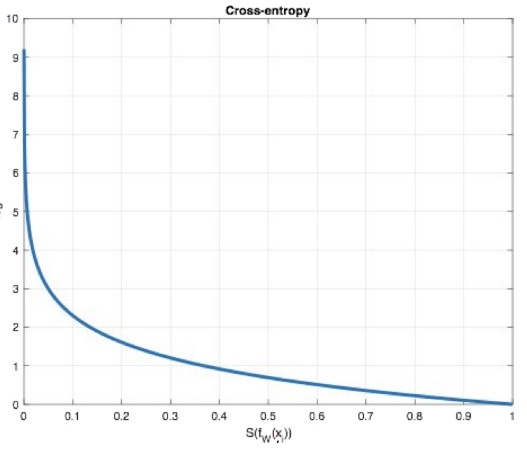
二分类任务损失函数

在处理二分类任务时，我们不再使用 softmax 激活函数，而是使用 sigmoid 激活函数，那损失函数也相应的进行调整，使用二分类的交叉熵损失函数：

L = - y \log \hat{y} - (1 - y) \log (1 - \hat{y})

其中：

y 是样本 x 属于某一个类别的真实概率
而 y^是样本属于某一类别的预测概率
L 用来衡量真实值 y 与预测值 y^之间差异性的损失结果。

网络优化方法

目标

知道梯度下降算法
知道网络训练过程中的 epoch, batch,iter
了解反向传播算法过程

梯度下降算法回顾

梯度下降法是一种寻找使损失函数最小化的方法。从数学上的角度来看，梯度的方向是函数增长速度最快的方向，那么梯度的反方向就是函数减少最快的方向，所以有：

w_{i j}^{new} = w_{i j}^{old} - η \frac{\partial E}{\partial w_{i j}}

其中，η是学习率，如果学习率太小，那么每次训练之后得到的效果都太小，增大训练的时间成本。如果，学习率太大，那就有可能直接跳过最优解，进入无限的训练中。解决的方法就是，学习率也需要随着训练的进行而变化。

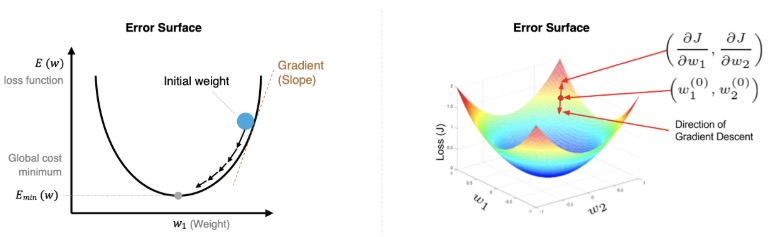
在进行模型训练时，有三个基础的概念：

1. Epoch: 使用全部数据对模型进行以此完整训练，训练轮次

2. Batch_size: 使用训练集中的小部分样本对模型权重进行以此反向传播的参数更新，每次训练每批次样本数量

3. Iteration: 使用一个 Batch 数据对模型进行一次参数更新的过程

假设数据集有 50000 个训练样本，现在选择 Batch Size = 256 对模型进行训练。

每个 Epoch 要训练的图片数量：50000

训练集具有的 Batch 个数：50000/256+1=196

每个 Epoch 具有的 Iteration 个数：196

10 个 Epoch 具有的 Iteration 个数：1960

总结

梯度下降算法的思想
网络优化，使损失函数最小的方法
网络训练中的三个概念
Epoch,batch,iter

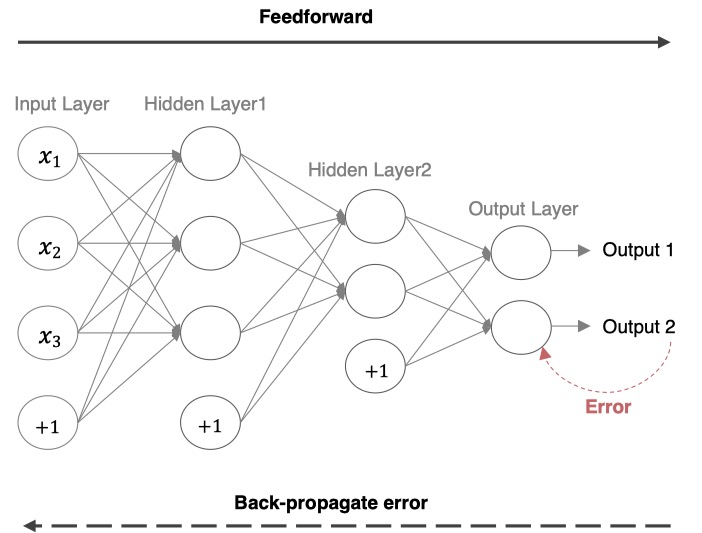
反向传播 (BP 算法)[了解]

前向传播：指的是数据输入的神经网络中，逐层向前传输，一直到运算到输出层为止。

反向传播（Back Propagation）：利用损失函数 ERROR，从后往前，结合梯度下降算法，依次求各个参数的偏导，

并进行参数更新

**反向传播对神经网络中的各个节点的权重进行更新。**一个简单的神经网络用来举例：激活函数为 sigmoid

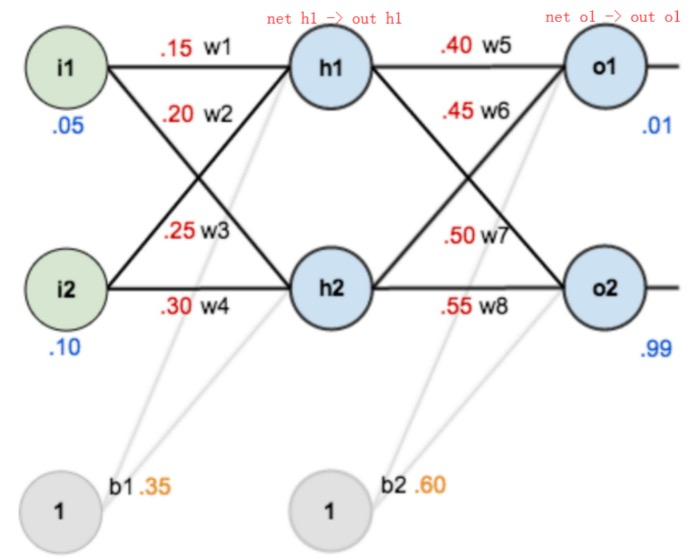
前向传播运算过程：

接下来是反向传播，我们先来求最简单的，求误差 E 对 w5 的导数。要求误差 E 对 w5 的导数，需要先求误差 E 对 out o1 的导数，再求 out o1 对 net o1 的导数，最后再求 net o1 对 w5 的导数，经过这个处理，我们就可以求出误差 E 对 w5 的导数（偏导），如下图所示：

导数（梯度）已经计算出来了，下面就是反向传播与参数更新过程：

如果要想求误差 E 对 w1 的导数，误差 E 对 w1 的求导路径不止一条，这会稍微复杂一点，但换汤不换药，计算过程如下

所示：

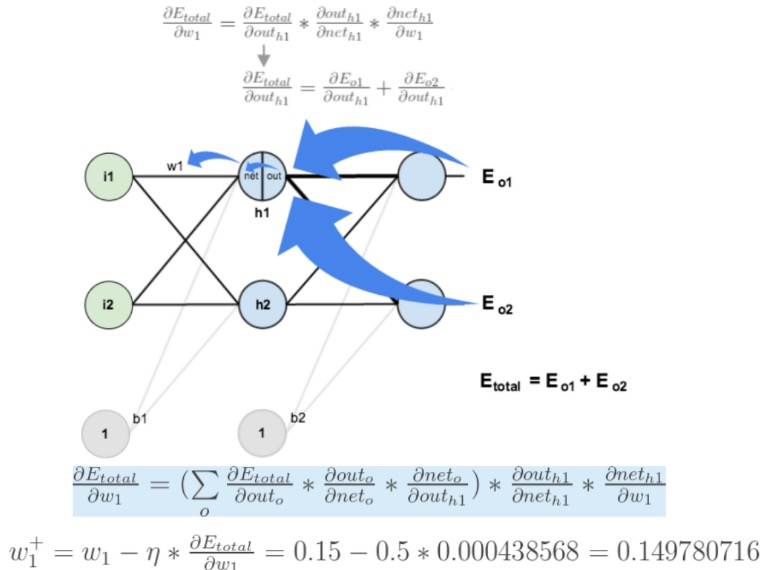
总结

1.前向传播和反向传播是什么？

前向传播：指的是数据输入的神经网络中，逐层向前传输，一直到运算到输出层为止。

反向传播（Back Propagation）：利用损失函数 ERROR，从后往前，结合梯度下降算法，依次求各个参数的偏导，并进行参数更新

案例 - 价格分类案例

掌握构建分类模型流程
动手实践整个过程

需求分析

小明创办了一家手机公司，他不知道如何估算手机产品的价格。为了解决这个问题，他收集了多家公司的手机销售数据。该数据为二手手机的各个性能的数据，最后根据这些性能得到 4 个价格区间，作为这些二手手机售出的价格区间。

主要包括：

battery-power：电池一次可储存的总能量，单位为毫安时
blue：是否有蓝牙
clock_speed：微处理器执行指令的速度
dual_sim：是否支持双卡
fc：前置摄像头百万像素
four_g:是否有4G
int_memory:内存（GB）
m_dep：移动深度（cm）
mobile_wt：手机重量
n_cores：处理器内核数
pc：主摄像头百万像素
px_height：像素分辨率高度
px_width：像素分辨率宽度
ram：随机存取存储器（兆字节）
sc_h：手机屏幕高度（cm）
sc_w：手机屏幕宽度（cm）
talk_time：一次电池充电持续时间最长的时间
three_g:是否有3G
touch_screen：是否有触控屏
wifi：是否能连wifi
price_range：价格区间（0，1，2，3)

我们需要帮助小明找出手机的功能（例如：RAM 等）与其售价之间的某种关系。我们可以使用机器学习的方法来解决这个问题，也可以构建一个全连接的网络。

需要注意的是：在这个问题中，我们不需要预测实际价格，而是一个价格范围，它的范围使用 0、1、2、3 来表示，所以该问题也是一个分类问题。接下来我们还是按照四个步骤来完成这个任务：

准备训练集数据
构建要使用的模型
模型训练
模型预测评估

导入所需的工具包

## 导入相关模块
import torch
from torch.utils.data import TensorDataset
from torch.utils.data import DataLoader
import torch.nn as nn
import torch.optim as optim
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import time

构建数据集

数据共有 2000 条，其中 1600 条数据作为训练集，400 条数据用作测试集。我们使用 sklearn 的数据集划分工作来完成。并使用 PyTorch 的 TensorDataset 来将数据集构建为 Dataset 对象，方便构造数据集加载对象。

python


## 构建数据集
def create_dataset():
    # 使用 pandas 读取数据
    data = pd.read_csv('data/手机价格预测.csv')
    # 特征值和目标值
    x, y = data.iloc[:, :-1], data.iloc[:, -1]
    # 类型转换：特征值，目标值
    x = x.astype(np.float32)
    y = y.astype(np.int64)
    # 数据集划分
    x_train, x_valid, y_train, y_valid = train_test_split(x, y, train_size=0.8, random_state=88)
    # 构建数据集，转换为 pytorch 的形式
    train_dataset = TensorDataset(torch.from_numpy(x_train.values), torch.tensor(y_train.values))
    valid_dataset = TensorDataset(torch.from_numpy(x_valid.values), torch.tensor(y_valid.values))
    # 返回结果
    return train_dataset, valid_dataset, x_train.shape[1], len(np.unique(y))

获取数据的结果

python

if __name__ == '__main__':
    # 获取数据
    train_dataset, valid_dataset, input_dim, class_num = create_dataset()
    print("输入特征数：", input_dim)
    print("分类个数：", class_num)

输出结果为：

输入特征数： 20
分类个数： 4

构建分类网络模型

构建全连接神经网络来进行手机价格分类，该网络主要由三个线性层来构建，使用 relu 激活函数。

网络共有 3 个全连接层，具体信息如下：第一层: 输入为维度为 20, 输出维度为: 128 第二层: 输入为维度为 128, 输出维度为: 256 第三层: 输入为维度为 256, 输出维度为: 4

python

## 构建网络模型
class PhonePriceModel(nn.Module):
    def __init__(self, input_dim, output_dim):
        super(PhonePriceModel, self).__init__()
        # 1. 第一层：输入为维度为 20, 输出维度为：128
        self.linear1 = nn.Linear(input_dim, 128)
        # 2. 第二层：输入为维度为 128, 输出维度为：256
        self.linear2 = nn.Linear(128, 256)
        # 3. 第三层：输入为维度为 256, 输出维度为：4
        self.linear3 = nn.Linear(256, output_dim)

    def forward(self, x):
        # 前向传播过程
        x = torch.relu(self.linear1(x))
        x = torch.relu(self.linear2(x))
        output = self.linear3(x)
        # 获取数据结果
        return output

模型实例化：

python

if __name__ == '__main__':
    # 模型实例化
    model = PhonePriceModel(input_dim, class_num)
    summary(model, input_size=(input_dim,), batch_size=16)

模型训练

网络编写完成之后，我们需要编写训练函数。所谓的训练函数，指的是输入数据读取、送入网络、计算损失、更新参数的流程，该流程较为固定。我们使用的是多分类交叉熵损失函数、使用 SGD 优化方法。最终，将训练好的模型持久化到磁盘中。

python

## 模型训练过程
def train(train_dataset, input_dim, class_num, ):
    # 初始化模型
    model = PhonePriceModel(input_dim, class_num)
    # 损失函数
    criterion = nn.CrossEntropyLoss()
    # 优化方法
    optimizer = optim.SGD(model.parameters(), lr=1e-3)
    # 训练轮数
    num_epoch = 50

编写训练函数

python

## 遍历每个轮次的数据
for epoch_idx in range(num_epoch):
    # 初始化数据加载器
    dataloader = DataLoader(train_dataset, shuffle=True, batch_size=8)
    # 训练时间
    start = time.time()
    # 计算损失
    total_loss = 0.0
    total_num = 1
    # 遍历每个 batch 数据进行处理
    for x, y in dataloader:
        # 将数据送入网络中进行预测
        output = model(x)
        # 计算损失
        loss = criterion(output, y)
        # 梯度清零
        optimizer.zero_grad()
        # 反向传播
        loss.backward()
        # 参数更新
        optimizer.step()
        # 损失计算
        total_num += 1
        total_loss += loss.item()
    # 打印损失变换结果
    print('epoch: %4s loss: %.2f, time: %.2fs' % (epoch_idx + 1, total_loss / total_num, time.time() - start))
## 模型保存
torch.save(model.state_dict(), 'model/phone.pth')

调用训练函数：

python

if __name__ == '__main__':
    # 获取数据
    train_dataset, valid_dataset, input_dim, class_num = create_dataset()
    # 模型训练过程
    train(train_dataset, input_dim, class_num)

训练结果如下所示：

编写评估函数

使用训练好的模型，对未知的样本的进行预测的过程。我们这里使用前面单独划分出来的验证集来进行评估。

python

def test(valid_dataset, input_dim, class_num):
    # 加载模型和训练好的网络参数
    model = PhonePriceModel(input_dim, class_num)
    model.load_state_dict(torch.load('data/phone.pth'))
    # 构建加载器
    dataloader = DataLoader(valid_dataset, batch_size=8, shuffle=False)
    # 评估测试集
    correct = 0
    # 遍历测试集中的数据
    for x, y in dataloader:
    # 将其送入网络中
    output = model(x)
    # 获取类别结果
    y_pred = torch.argmax(output, dim=1)
    # 获取预测正确的个数
    correct += (y_pred == y).sum()
    # 求预测精度
    print('Acc: %.5f' % (correct.item() / len(valid_dataset)))


if __name__ == '__main__':
    # 获取数据
    train_dataset, valid_dataset, input_dim, class_num = create_dataset()
    # 模型预测结果
    test(valid_dataset, input_dim, class_num)

输出结果： Acc: 0.54750

总结

1.案例的整体流程是： • 数据集构建 • 模型构建 • 模型训练 • 模型预测

神经网络基础 ​

神经网络 ​

激活函数 ​

sigmoid 激活函数 ​

ReLU 激活函数 ​

SoftMax 激活函数 ​

其他常见的激活函数 ​

激活函数的选择方法 ​

总结 ​

神经网络搭建和参数计算 ​

神经网络的优缺点 ​

损失函数 ​

什么是损失函数 ​

多分类损失函数 ​

二分类任务损失函数 ​

网络优化方法 ​

梯度下降算法回顾 ​

反向传播 (BP 算法)[了解] ​

案例 - 价格分类案例 ​

需求分析 ​

导入所需的工具包 ​

构建数据集 ​

获取数据的结果 ​

构建分类网络模型 ​

模型训练 ​

编写训练函数 ​

编写评估函数 ​

神经网络基础

神经网络

激活函数

sigmoid 激活函数

ReLU 激活函数

SoftMax 激活函数

其他常见的激活函数

激活函数的选择方法

总结

神经网络搭建和参数计算

神经网络的优缺点

损失函数

什么是损失函数

多分类损失函数

二分类任务损失函数

网络优化方法

梯度下降算法回顾

反向传播 (BP 算法)[了解]

案例 - 价格分类案例

需求分析

导入所需的工具包

构建数据集

获取数据的结果

构建分类网络模型

模型训练

编写训练函数

编写评估函数