K-近算法邻
k-近邻(K Nearest Neighbor)算法是一个有监督的机器学习算法。k-近邻算法也称为 knn 算法,可以解决分类问题,也可以解决回归问题。这个算法是机器学习里面一个比较经典的算法, 总体来说 KNN 算法是相对比较容易理解的算法
定义
如果一个样本在特征空间中的 k 个最相似 (即特征空间中最邻近) 的样本中的大多数属于某一个类别,则该样本也属于这个类别。
根据你的“邻居”来推断出你的类别,可以总结为一句话 “离谁近,就是谁”
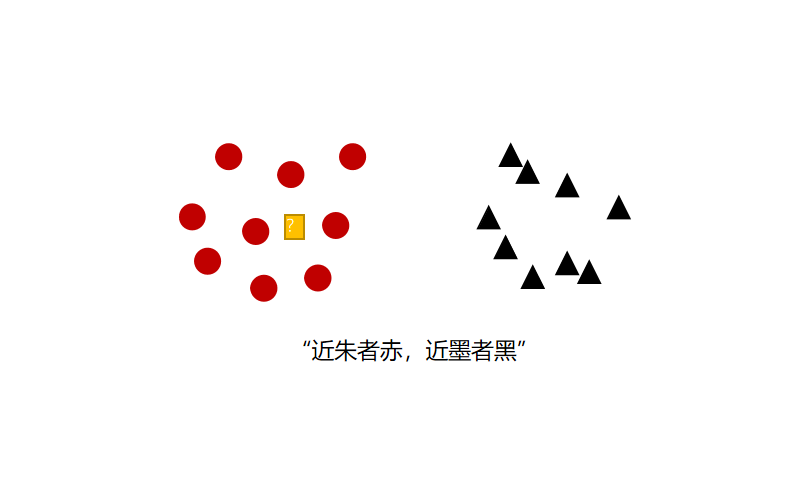
KNN 算法原理
k-近邻算法的核心思想是未标记样本的类别,由距离其最近的 k 个邻居投票来决定。
假设,我们有一个已经标记的数据集,即已经知道了数据集中每个样本所属的类别。此时,有一个未标记的数据样本,我们的任务是预测出这个数据样本所属的类别。k-近邻算法的原理是,计算待标记的数据样本和数据集中每个样本的距离,取距离最近的 k 个样本。待标记的数据样本所属的类别,就由这 k 个距离最近的样本投票产生。
KNN 算法流程
1)计算已知类别数据集中的点与当前点之间的距离
2)按距离递增次序排序
3)选取与当前点距离最小的 k 个点
4)统计前 k 个点所在的类别出现的频率
5)返回前 k 个点出现频率最高的类别作为当前点的预测分类
K-近邻算法简介
- 定义:就是通过你的"邻居"来判断你属于哪个类别
- 如何计算你到你的"邻居"的距离:一般时候,都是使用欧氏距离
案例:预测汽车类型(分类问题)
根据汽车的大小,预测汽车属于什么类型
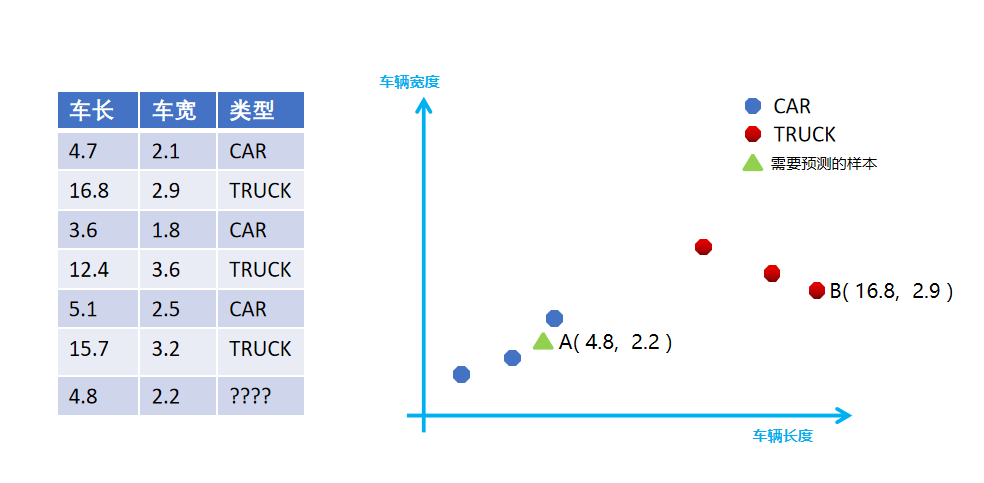
首先需要计算最后一辆车到其他汽车的欧氏距离
import math
train = [
{'length': 4.7, 'width': 2.1, 'cate': 'CAR'},
{'length': 5.1, 'width': 2.5, 'cate': 'CAR'},
{'length': 3.6, 'width': 1.8, 'cate': 'CAR'},
{'length': 12.4, 'width': 3.6, 'cate': 'TRUCK'},
{'length': 16.8, 'width': 2.9, 'cate': 'TRUCK'},
{'length': 15.7, 'width': 3.2, 'cate': 'TRUCK'},
]
target = {'length': 4.8, 'width': 2.2, 'cate': ''}
# 计算 预测点到所有点的距离
predict = []
for x in train:
ret = math.sqrt((target['length'] - x['length']) ** 2 + (target['width'] - x['width']) ** 2)
predict.append([ret, x['cate']])
predict.sort()
print(predict)算法优缺点
优点:准确性高,对异常值和噪声有较高的容忍度。
缺点:计算量较大,对内存的需求也较大。从算法原理可以看出来,每次对一个未标记样本进行分类时,都需要全部计算一遍距离。
算法参数
其算法参数是 k,参数选择需要根据数据来决定。k 值越大,模型的偏差越大,对噪声数据越不敏感,当 k 值很大时,可能造成模型欠拟合;k 值越小,模型的方差就会越大,当 k 值太小,就会造成模型过拟合。
算法的变种
k-近邻算法有一些变种,其中之一就是可以增加邻居的权重。默认情况下,在计算距离时,都是使用相同权重。实际上,我们可以针对不同的邻居指定不同的距离权重,如距离越近权重越高。这个可以通过指定算法的 weights 参数来实现。
另外一个变种是,使用一定半径内的点取代距离最近的 k 个点。在 scikit-learn 里,RadiusNeighborsClassifier 类实现了这个算法的变种。当数据采样不均匀时,该算法变种可以取得更好的性能。
K-近邻算法 API
sklearn.neighbors.KNeighborsClassifier(n_neighbors=5)
n_neighbors:int,可选(默认= 5),k_neighbors 查询默认使用的邻居数
sklearn knn
步骤分析
- 获取数据集
- 数据基本处理(该案例中省略)
- 特征工程(该案例中省略)
- 机器学习
- 模型评估(该案例中省略)
import matplotlib.pyplot as plt
import numpy as np
import pandas
# 导入 K 近邻算法模型
from sklearn.neighbors import KNeighborsClassifier
# 1. 获取数据集
car_data = [
{'length': 4.7, 'width': 2.1, 'cate': 'CAR'},
{'length': 5.1, 'width': 2.5, 'cate': 'CAR'},
{'length': 3.6, 'width': 1.8, 'cate': 'CAR'},
{'length': 12.4, 'width': 3.6, 'cate': 'TRUCK'},
{'length': 16.8, 'width': 2.9, 'cate': 'TRUCK'},
{'length': 15.7, 'width': 3.2, 'cate': 'TRUCK'},
]
# 2. 进行基本的处理(略)
df = pandas.DataFrame(data=car_data)
# 3. 特征工程(略)
target = {'length': 4.8, 'width': 2.2, 'cate': ''}
print(df[['length', 'width']])
df_car = df[df['cate'] == 'CAR']
df_truck = df[df['cate'] == 'TRUCK']
# 绘制图表对照查看(课省略)
print(df_car)
plt.scatter(df_car.length, df_car.width)
plt.scatter(df_truck.length, df_truck.width)
plt.scatter([4.8], [2.2])
plt.show()
# 4. 机器学习
# 实例化 API
estimator = KNeighborsClassifier(n_neighbors=1)
# 使用 fit 方法进行训练 自动学习
estimator.fit(df[['length', 'width']], df.cate)
# 使用模型预测结果
print(estimator.predict([[4.8, 2.2]]))
# 5. 模型评估(略)问题
距离公式,除了欧式距离,还有哪些距离公式可以使用?
选取 K 值的大小?
API 中其他参数的具体含义?
小案例
导入模块
from sklearn.neighbors import KNeighborsClassifier构造数据集
x = [[50], [60], [80], [100]]
y = ['普通', '合格', '优秀', '完美']机器学习 -- 模型训练
# 实例化 API
estimator = KNeighborsClassifier(n_neighbors=2)
# 使用 fit 方法进行训练
estimator.fit(x, y)
estimator.predict([[1]])电影类型分析(案例)
假设我们现在有几部电影
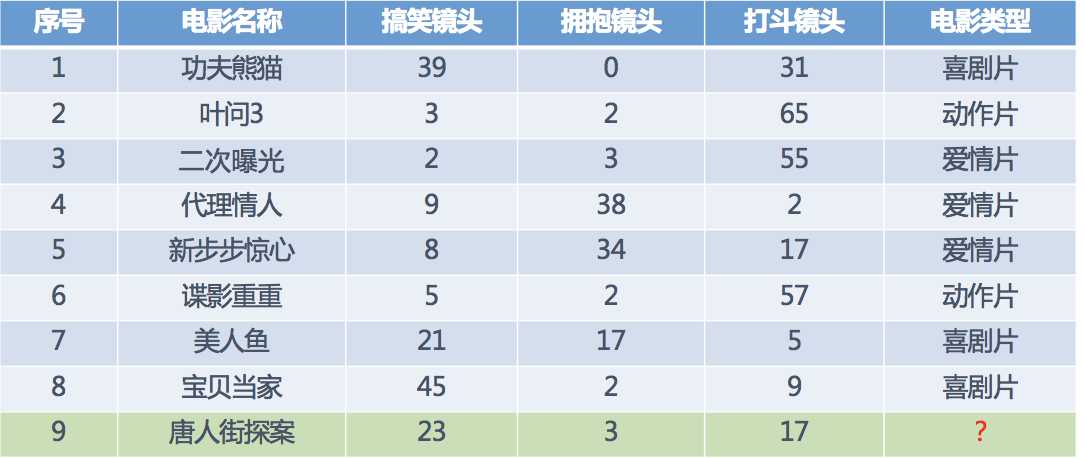
其中 9 号电影不知道类别,如何去预测?我们可以利用 K 近邻算法的思想
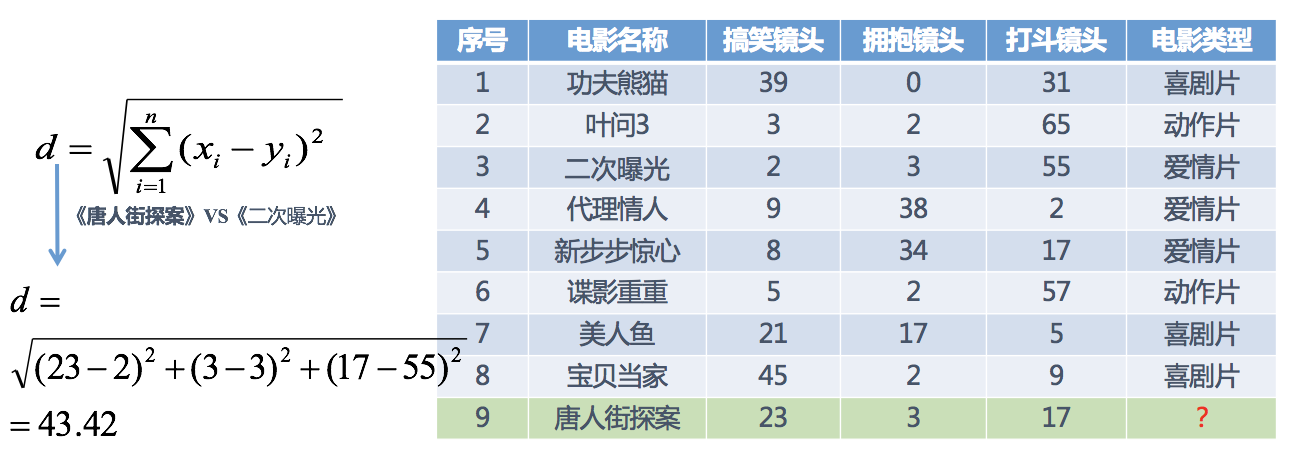
分别计算每个电影和被预测电影的距离,然后求解

k 值的选择
K 值选择说明
举例说明:

- K 值过小
- 容易受到异常点的影响
- k 值过大
- 受到样本均衡的问题
K 值选择问题,李航博士的一书「统计学习方法」上所说:
选择较小的 K 值,就相当于用较小的领域中的训练实例进行预测,“学习”近似误差会减小,只有与输入实例较近或相似的训练实例才会对预测结果起作用,与此同时带来的问题是“学习”的估计误差会增大,换句话说, K 值的减小就意味着整体模型变得复杂,容易发生过拟合;
选择较大的 K 值,就相当于用较大领域中的训练实例进行预测,其优点是可以减少学习的估计误差,但缺点是学习的近似误差会增大。这时候, 与输入实例较远(不相似的)训练实例也会对预测器作用,使预测发生错误,且 K 值的增大就意味着整体的模型变得简单。
K=N(N 为训练样本个数),则完全不足取,因为此时无论输入实例是什么,都只是简单的预测它属于在训练实例中最多的类,模型过于简单,忽略了训练实例中大量有用信息。
在实际应用中,K 值一般取一个比较小的数值,例如采用交叉验证法(简单来说,就是把训练数据在分成两组:训练集和验证集)来选择最优的 K 值。
- 近似误差:
- 对现有训练集的训练误差,关注训练集,
- 如果近似误差过小可能会出现过拟合的现象,对现有的训练集能有很好的预测,但是对未知的测试样本将会出现较大偏差的预测。
- 模型本身不是最接近最佳模型。
- 估计误差:
- 可以理解为对测试集的测试误差,关注测试集,
- 估计误差小说明对未知数据的预测能力好,
- 模型本身最接近最佳模型。
总结:
- KNN 中 K 值大小选择对模型的影响【知道】
- K 值过小:
- 容易受到异常点的影响
- 容易过拟合
- k 值过大:
- 受到样本均衡的问题
- 容易欠拟合
- K 值过小: