正心全栈编程-文档站

Appearance

如何在 sklearn 中使用 SVM ​

在 Python 的 sklearn 工具包中有 SVM 算法，首先需要引用工具包：

from sklearn import svm

SVM 既可以做回归，也可以做分类。

当用 SVM 做回归的时候，可以使用 SVR 或 LinearSVR。SVR 的英文是 Support Vector Regression。

当做分类器的时候，我们使用的是 SVC 或者 LinearSVC。SVC 的 英文是 Support Vector Classification。

从名字上你能看出 LinearSVC 是个线性分类器，用于处理线性可分的数据，只能使用线性核函数。SVM 是通过核函数将样本从原始空间映射到一个更高维的特质空间中，这样就使得样本在新的空间中线性可分。

如果是针对非线性的数据，需要用到 SVC。在 SVC 中，我们既可以使用到线性核函数（进行线性划分），也能使用高维的核函数（进行非线性划分）。

kernel 代表核函数的选择，它有四种选择，只不过默认是 rbf，即高斯核函数。

  1. linear：线性核函数
  2. poly：多项式核函数
  3. rbf：高斯核函数（默认）
  4. sigmoid：sigmoid 核函数

这四种函数代表不同的映射方式，在实际工作中，如何选择这 4 种核函数呢？

  • 线性核函数，是在数据线性可分的情况下使用的，运算速度快，效果好。不足在于它不能处理线性不可分的数据。

  • 多项式核函数可以将数据从低维空间映射到高维空间，但参数比较多，计算量大。

  • 高斯核函数同样可以将样本映射到高维空间，但相比于多项式核函数来说所需的参数比较少，通常性能不错，所以是默认使用的核函数。

  • sigmoid 经常用在神经网络的映射中。因此当选用 sigmoid 核函数时，SVM 实现的是多层神经网络。

上面介绍的 4 种核函数，除了第一种线性核函数外，其余 3 种都可以处理线性不可分的数据。

如何创建一个 SVM 分类器呢？ ​

我们首先使用 SVC 的构造函数：model = svm.SVC(kernel=‘rbf’, C=1.0, gamma=‘auto’)，这里有三个重要的参数 kernel、C 和 gamma。

参数 C 代表目标函数的惩罚系数，惩罚系数指的是分错样本时的惩罚程度，默认情况下为 1.0。当 C 越大的时候，分类器的准确性越高，但同样容错率会越低，泛化能力会变差。相反，C 越小，泛化能力越强，但是准确性会降低。

参数 gamma 代表核函数的系数，默认为样本特征数的倒数，即 gamma = 1 / n_features。

在创建 SVM 分类器之后，就可以输入训练集对它进行训练。我们使用 model.fit(train_X,train_y)，传入训练集中的特征值矩阵 train_X 和分类标识 train_y。特征值矩阵就是我们在特征选择后抽取的特征值矩阵；分类标识就是人工事先针对每个样本标识的分类结果。这样模型会自动进行分类器的训练。我们可以使用 prediction=model.predict(test_X) 来对结果进行预测，传入测试集中的样本特征矩阵 test_X，可以得到测试集的预测分类结果 prediction。

同样也可以创建线性 SVM 分类器，使用 model=svm.LinearSVC()。在 LinearSVC 中没有 kernel 这个参数，限制我们只能使用线性核函数。由于 LinearSVC 对线性分类做了优化，对于数据量大的线性可分问题，使用 LinearSVC 的效率要高于 SVC。

如果你不知道数据集是否为线性，可以直接使用 SVC 类创建 SVM 分类器。

python
import numpy as np
from matplotlib import pyplot as plt
from sklearn import svm
from sklearn.datasets import make_blobs


def plot_hyperplane(clf, X, y,
                    h=0.02,
                    draw_sv=True,
                    title='hyperplan'):
    # create a mesh to plot in
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                         np.arange(y_min, y_max, h))

    plt.title(title)
    plt.xlim(xx.min(), xx.max())
    plt.ylim(yy.min(), yy.max())
    plt.xticks(())
    plt.yticks(())

    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    # Put the result into a color plot
    Z = Z.reshape(xx.shape)
    plt.contourf(xx, yy, Z, cmap='hot', alpha=0.5)

    markers = ['o', 's', '^']
    colors = ['b', 'r', 'c']
    labels = np.unique(y)
    for label in labels:
        plt.scatter(X[y == label][:, 0],
                    X[y == label][:, 1],
                    c=colors[label],
                    marker=markers[label])
    if draw_sv:
        sv = clf.support_vectors_
        plt.scatter(sv[:, 0], sv[:, 1], c='y', marker='x')


X, y = make_blobs(n_samples=100, centers=3,
                  random_state=0, cluster_std=0.8)

clf_linear = svm.SVC(C=1.0, kernel='linear')
clf_poly = svm.SVC(C=1.0, kernel='poly', degree=3)
clf_rbf = svm.SVC(C=1.0, kernel='rbf', gamma=0.5)
clf_rbf2 = svm.SVC(C=1.0, kernel='rbf', gamma=0.1)

plt.figure(figsize=(10, 10), dpi=144)

clfs = [clf_linear, clf_poly, clf_rbf, clf_rbf2]
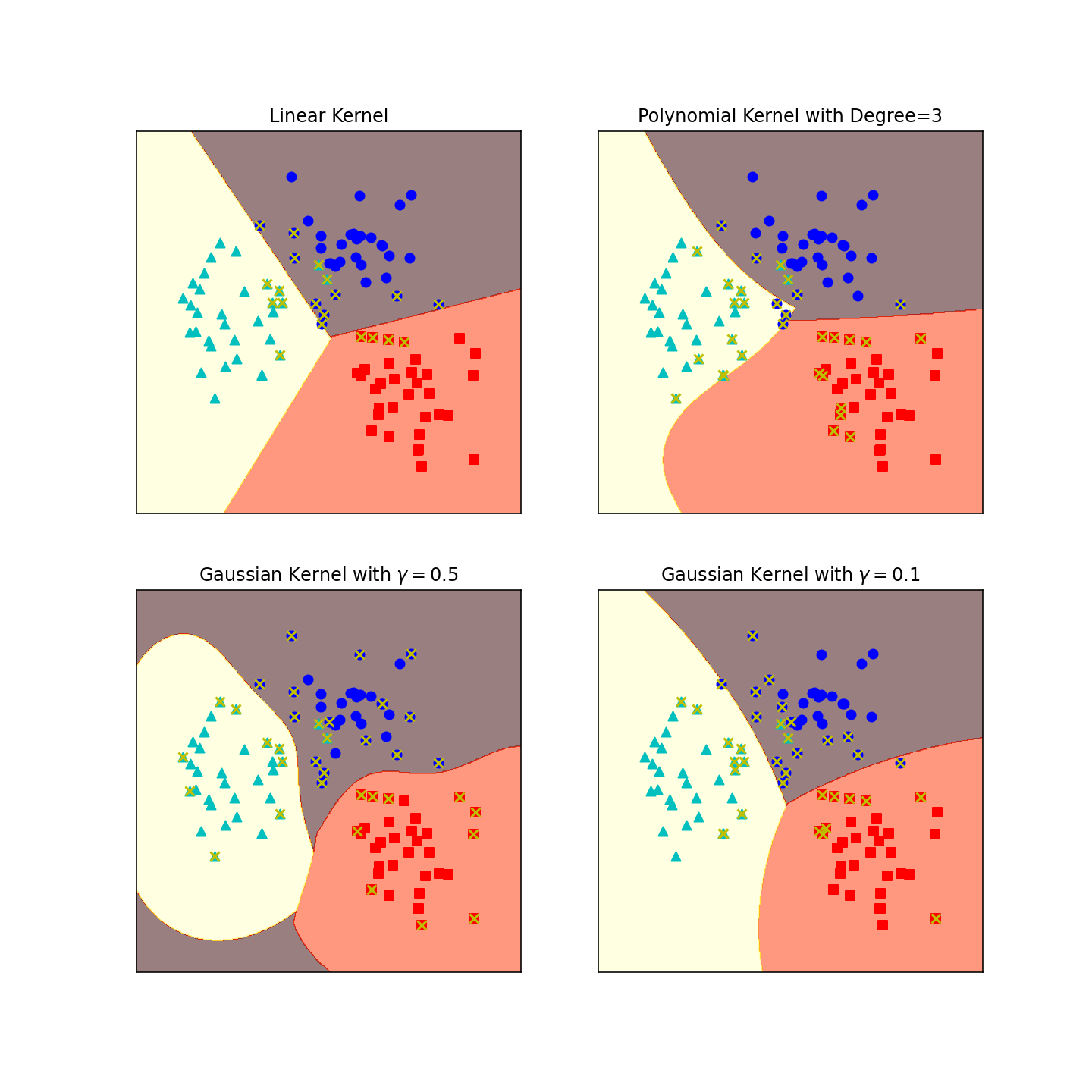
titles = ['Linear Kernel',
          'Polynomial Kernel with Degree=3',
          'Gaussian Kernel with $\gamma=0.5$',
          'Gaussian Kernel with $\gamma=0.1$']
for clf, i in zip(clfs, range(len(clfs))):
    clf.fit(X, y)
    plt.subplot(2, 2, i + 1)
    plot_hyperplane(clf, X, y, title=titles[i])
plt.show()

image-20210914144639999