PCA 算法

PCA 是 Principal Component Analysis 的缩写，中文称为主成分分析法。它是一种维数约减（Dimensionality Reduction）算法，即把[高维度数据]在[损失最小]的情况下转换为[低维度数据]的算法。显然，PCA 可以用来对数据进行压缩，可以在可控的失真范围内提高运算速度。本节涵盖的内容如下：

• PCA 算法的原理及运算步骤；

• 使用 Numpy 实现简化版的 PCA 算法，并与 scikit-learn 的结果进行比较；

• PCA 的物理含义；

• PCA 的数据还原率及应用；

• 通过一个人脸识别程序观察 PCA 的重要作用实例。

算法原理

我们先从最简单的情况谈起。假设需要把一个二维数据减为一维数据，要怎么做呢？

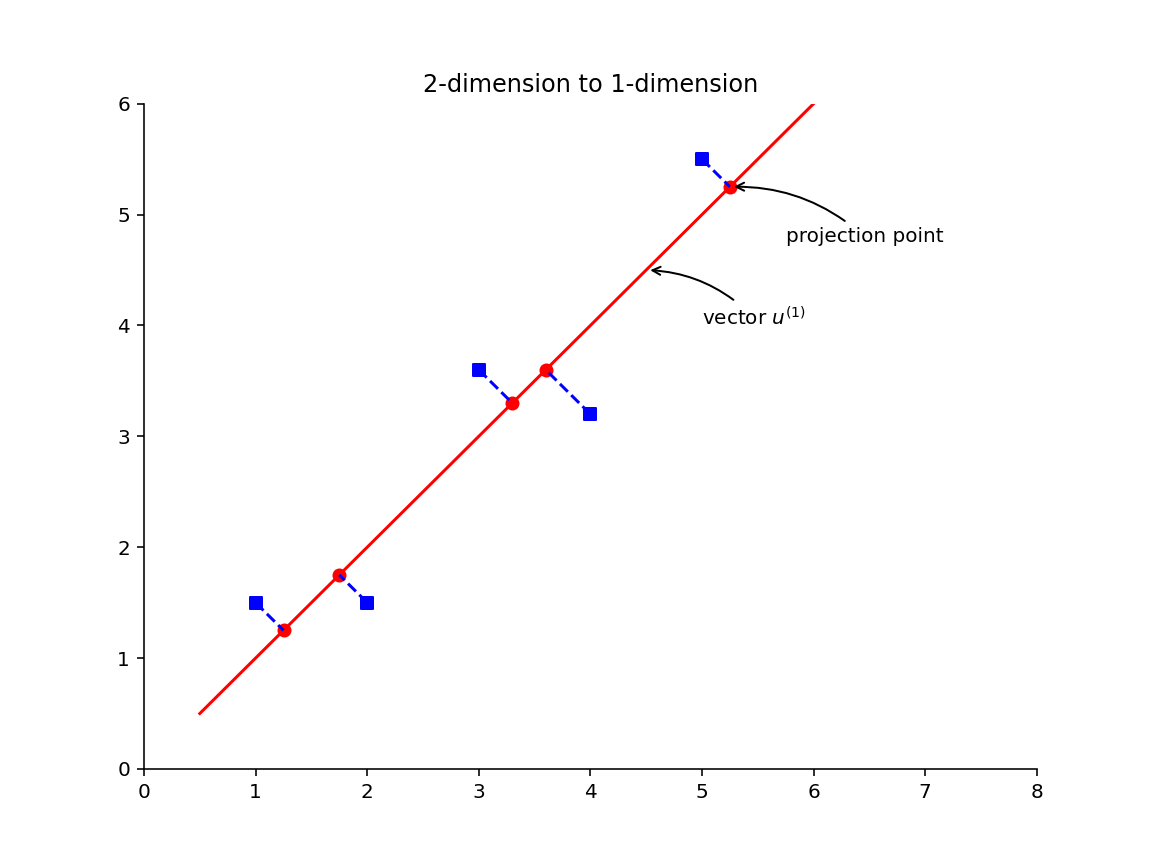
我们可以想办法找出一个向量 $u^{(1)}$，以便让二维数据的点（方形点）到这个向量所在的直线上的 平均距离最短，即投射误差最小。

这样就可以在失真最小的情况下，把二维数据转换为向量 $u^{(1)}$ 所在直线上的一维数据。再进一步，假如需要把三维数据降为二维数据时，我们需要找出两个向量 $u^{(1)}$， $u^{(2)}$，以便让三维数据的点在这两个向量所决定的平面上的投射误差最小。

如果从数学角度来一般地描述 PCA 算法就是，当需要从 n 维数据降为 k 维数据时，需要找出 k 个向量 $u^{(1)},u^{(2)},\dots ,u^{(k)}$，把 n 维的数据投射到这 k 个向量决定的线性空间里，最终使投射误差最小化的过程。

思考：什么情况下，进行 PCA 运算时误差为 0？当这些二维数据在同一条直线上时，进行 PCA 运算后，误差为 0。

问题来了，怎样找出投射误差最小的 k 个向量呢？要完整地用数学公式推导出这个方法，涉及较多高级线性代数的知识我们就此略过。感兴趣的读者可进一步阅读本章扩展阅读部分的内容。下面我们直接介绍 PCA 算法求解的一般步骤。

假设有一个数据集，用 $m\times n$ 维的矩阵 A 表示。矩阵中每一行表示一个样本，每一列表示一个特征，总共有 $m$ 个样本，每个样本有 $n$ 个特征。我们的目标是减少特征个数，只保留最重要的个 $k$ 特征。

数据归一化和缩放

数据归一化和缩放是一种数学技巧，旨在提高 PCA 运算时的效率。数据归一化的目标是使特征的均值为 0。数据归一化公式为：

$$x_j^{(i)}=a_j^{(i)}-{\mu }_j$$

其中，$a_j^{(i)}$ 是指 i 个样本的第 j 个特征的值，${\mu }_j$ 表示的是第 j 个特征的均值。当不同的特征值不在同一个数量级上的时候，还需要对数据进行缩放。数据归一化再缩放的公式为：

$$x_j^{(i)}=\frac{a_j^{(i)}-{\mu }_j}{s_j}$$

其中，$a_j^{(i)}$ 是指 $i$ 个样本的第 j 个特征的值，${\mu }_j$ 表示的是第 $j$ 个特征的均值，$s_j$ 表示第 $j$ 个特征的范围，即 $s_j=max(a_j^{(i)})-min(a_j^{(i)})$

计算协方差矩阵的特征向量

针对预处理后的矩阵 X，先计算其 协方差矩阵（Covariance Matrix）：

$$\sum =\frac{1}{m}{X}^{T}X$$

其中，$\sum$ 表示协方差矩阵，用大写的 Sigma 表示，大写的 Sigma 和累加运算符看起来几乎一样，但这里其实是一个数学符号而已，不是累加运算。计算结果 $\sum$ 将是一个 $n\times n$ 的矩阵

接着通过奇异值分解来计算协方差矩阵的 特征向量 （eigenvectors）：

$$[U,S,V]=svd(\sum )$$

其中，$svd$ 是奇异值分解（Singular Value Decomposition）运算，是高级线性代数的内容。经过奇异值分解后，有 3 个返回值，其中矩阵 $U$ 是个 $n\times n$ 的矩阵，如果我们选择 $U$ 的列作为向量，那么我们将得到 $n$ 个列向量 $u^{(1)},u^{(2)},\dots ,u^{(n)}$ ，这些向量就是协方差矩阵的特征向量。它表示的物理意义是，协方差矩阵Σ可以由这些特征向量进行线性组合得到。

数据降维和恢复

得到特征矩阵后，就可以对数据进行降维处理了。假设降维前的值为 $x^{(i)}$ ，降维后为 $z^{(i)}$ ，那么：

$$z^{(i)}=U_{reduce}^T{x}^{(i)}$$

其中，$U_{reduce}=[u^{(}1)，u^{(}2)，\dots ，u^{(}k)]$，它选取自矩阵 $U$ 的前 $k$ 个向量，$U_{reduce}$ 称为 主成分特征矩阵 ，它是数据降维和恢复的关键中间变量。看一下数据维度，$U_{reduce}$ 是 $n\times k$ 的矩阵，因此 $U_{reduce}^T$ 是 $k\times n$ 的矩阵，$x^{(}i)$ 是 $n\times 1$ 的向量，因此 $z^{(i)}$ 是 $k\times 1$ 的向量。这样即完成了数据的降维操作。

也可以用矩阵运算一次性转换多个向量，提高效率。假设 $X$ 是行向量 $x^{(i)}$ 组成的矩阵，则：

$$Z=X{U}_{reduce}$$

其中，X 是 m×n 的矩阵，因此降维后的矩阵 Z 也是一个 m×k 的矩阵。

从物理意义角度来看， $Z^{(i)}$ 就是 $x^{(i)}$ 在 $U_{reduce}$ 构成的线性空间投射，并且其投射误差最小。要从数学上证明这个结论，将是一个非常复杂的过程。对其原理感兴趣的读者可以参阅本章的扩展阅读。

数据降维后，怎样恢复呢？从前面的计算公式我们知道，降维的数据计算公式 $z^{(i)}=U_{reduce}^T{x}^{(i)}$ 所以，如果要还原数据，可以使用下面的公式：

$$X_{approx}=U_{reduce}{Z}^{(i)}$$

其中， $U_{reduce}$ 是 $n\times k$ 维矩阵， $Z^{(i)}$ 是 $k$ 维列向量。这样算出来的 $x^{(i)}$ 就是 $n$ 维列向量。

矩阵化数据恢复运算公式为：

$$X_{approx}=Z{U}_{reduce}^T$$

其中，$X_{approx}$ 是还原回来的数据，是一个 $m\times n$ 的矩阵，每行表示一个训练样例。$Z$ 是一个 $m\times k$ 的矩阵，是降维后的数据。

PCA 算法示例

假设我们的数据集总共有 5 个记录，每个记录有 2 个特征，这样构成的矩阵 A 为：

我们的目标是把二维数据降为一维数据。为了更好地理解 PCA 的计算过程，分别使用 Numpy 和 sklearn 对同一个数据进行 PCA 降维处理。

使用 Numpy 模拟 PCA 计算过程

下面我们使用 Numpy 来模拟 PCA 降维的过程。首先需要对数据进行预处理：

import numpy as np

A = np.array([[3, 2000],
              [2, 3000],
              [4, 5000],
              [5, 8000],
              [1, 2000]], dtype='float')
# 数据归一化
mean = np.mean(A, axis=0)
norm = A - mean
# 数据缩放
scope = np.max(norm, axis=0) - np.min(norm, axis=0)
norm = norm / scope
print(norm)

由于两个特征的均值不在同一个数量级，我们同时对数据进行了缩放。在笔者的计算机上输出如下：

array([[ 0.        , -0.33333333],
       [-0.25      , -0.16666667],
       [ 0.25      ,  0.16666667],
       [ 0.5       ,  0.66666667],
       [-0.5       , -0.33333333]])

接着对协方差矩阵进行奇异值分解，求解其特征向量：

# 协方差求奇异值
U, S, V = np.linalg.svd(np.dot(norm.T, norm))
print(U)

在计算机上的输出如下：

[[-0.67710949 -0.73588229]
 [-0.73588229  0.67710949]]

由于需要把二维数据降为一维，因此只取特征矩阵的第一列来构造出 Ureduce：

# 二维数据降为一维
U_reduce = U[:, 0].reshape(2, 1)
print(U_reduce)

其输出如下：

array([[-0.67710949],
       [-0.73588229]])

有了主成份特征矩阵，就可以对数据进行降维了：

# 降维
R = np.dot(norm, U_reduce)
print(R)

其输出如下：

[[ 0.2452941 ]
 [ 0.29192442]
 [-0.29192442]
 [-0.82914294]
 [ 0.58384884]]

这样就把二维的数据降维为一维的数据了。如果需要还原数据，依照 PCA 数据恢复的计算公式，可得：

# 数据恢复
Z = np.dot(R, U_reduce.T)
print(Z)

输出结果如下

[[-0.16609096 -0.18050758]
 [-0.19766479 -0.21482201]
 [ 0.19766479  0.21482201]
 [ 0.56142055  0.6101516 ]
 [-0.39532959 -0.42964402]]

由于我们在数据预处理阶段对数据进行了归一化，并且做了缩放处理，所以需要进一步还原才能得到原始数据，这一步是数据预处理的逆运算。

# 数据预处理的逆运算
print(np.multiply(Z, scope) + mean)

其中，numpy.multiply 是矩阵的点乘运算，即对应的元素相乘。对矩阵基础不熟悉的读者，可以搜索矩阵点乘和叉乘的区别。上述代码的输出如下：

[[2.33563616e+00 2.91695452e+03]
 [2.20934082e+00 2.71106794e+03]
 [3.79065918e+00 5.28893206e+03]
 [5.24568220e+00 7.66090960e+03]
 [1.41868164e+00 1.42213588e+03]]

与原始矩阵 A 相比，恢复后的数据还是存在一定程度的失真，这种失真是不可避免的。个别读者可能会对 2.91695452e+03 数值感到奇怪，实际上它是一种科学计数法，e+03 表示的是 10 的 3 次方，其表示的数值是 2916.95452。

使用 sklearn 进行 PCA 降维运算

在 sklearn 工具包里，类 sklearn.decomposition.PCA 实现了 PCA 算法，使用方便，不需要了解具体的 PCA 运算步骤。但需要注意的是，数据的预处理需要自己完成，其 PCA 算法实现本身不进行数据预处理 (归一化和缩放)。此处，我们选择 MinMaxScaler 类进行数据预处理。

import numpy as np
from sklearn.decomposition import PCA
from sklearn.preprocessing import MinMaxScaler

A = np.array([[3, 2000],
              [2, 3000],
              [4, 5000],
              [5, 8000],
              [1, 2000]], dtype='float')

# 数据归一化
scaler = MinMaxScaler()
A = scaler.fit_transform(A)
print(A)

# PCA 数据降维
pca = PCA(n_components=1)
R2 = pca.fit_transform(A)
print(R2)

# 恢复数据
print(pca.inverse_transform(R2))

阅读过前面章节的读者，对 Pipeline 应该不会陌生，它的作用是把数据预处理和 PCA 算法组成一个串行流水线。这段代码在笔者计算机上的输出如下：

array([[-0.2452941 ],
       [-0.29192442],
       [ 0.29192442],
       [ 0.82914294],
       [-0.58384884]])

这个输出值就是矩阵 A 经过预处理及 PCA 降维后的数值。细心的读者会发现，此处的输出和 10.2.1 节使用 Numpy 降维后的输出刚好符号相反。这其实不是错误，只是降维后大家选择的坐标方向不同而已。

接着我们在 sklearn 里把数据恢复回来：

# 恢复数据
print(pca.inverse_transform(R2))

这里的 pca 是一个 Pipeline 实例，其逆运算 inverse_transform() 是逐级进行的，即先进行 PCA 还原，再执行预处理的逆运算。具体来说就是先调用 PCA.inverse_transform()，然后再调用 MinMaxScaler.inverse_transform()。其输出如下：

[[2.33563616e+00 2.91695452e+03]
 [2.20934082e+00 2.71106794e+03]
 [3.79065918e+00 5.28893206e+03]
 [5.24568220e+00 7.66090960e+03]
 [1.41868164e+00 1.42213588e+03]]

PCA 的物理含义

我们可以把前面例子中的数据在一个坐标轴上全部画出来，从而仔细地观察 PCA 降维过程的物理含义

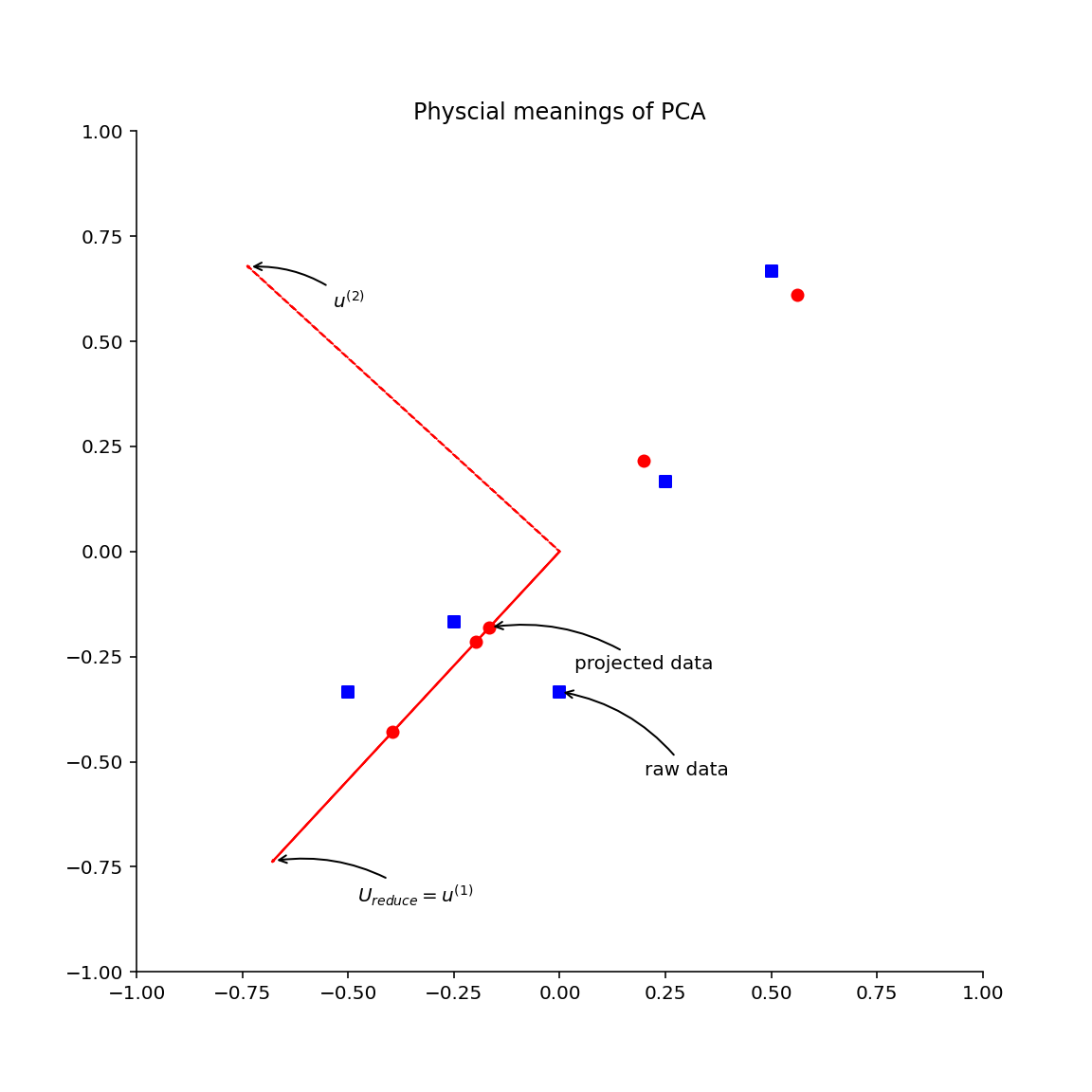
图中正方形的点是原始数据经过预处理后 (归一化、缩放) 的数据，圆形的点是从一维恢复到二维后的数据。

同时，我们画出主成分特征向量 u^(1)^，u^(2)^，根据图的直观印象，介绍几个有意思的结论：

首先，圆形点实际上就是方形点在向量 u^(1)^ 所在的直线上的投射点，所谓的降维，实际上就是方形的点在主成分特征向量 u^(1) ^上的投影。所谓的 PCA 数据恢复，并不是真正的恢复，只是把降维后的坐标转换为原坐标系中的坐标而已。

针对我们的例子，只是把由向量 u^(1)^ 决定的一维坐标系中的坐标转换为原始二维坐标系中的坐标。其次，主成分特征向量 u^(1)^，u^( 2)^ 是相互垂直的。再次，方形点和圆形点之间的距离，就是 PCA 数据降维后的误差。

PCA 的数据还原率及应用

PCA 算法可以用来对数据进行压缩，可以在可控的失真范围内提高运算速度。

数据还原率

使用 PCA 对数据进行压缩时，涉及失真的度量问题，即压缩后的数据能在多大程度上还原出原数据，我们称这一指标为 [数据还原率] ，用百分比表示。假设我们要求失真度不超过 1%，即数据还原率达到 99%，怎样来实现这个要求呢？k 是主成分分析法中主成分的个数。可以用下面的公式作为约束条件，从而选择合适的误差范围下，最合适的 k 值：

$$\begin{gathered} \frac{ \\ \frac{1}{m}\sum _{i=1}^m||x^{(i)}-x_{approx}^{(i)}|{|}^2 \\ }{ \\ \frac{1}{m}\sum _{i=1}^m||x^{(i)}||}\le 0.01 \end{gathered}$$

其中，分子部分表示平均投射误差的平方；分母部分表示所有训练样例到原点距离的平均值。这里的物理意义用术语可以描述为 [99% 的数据真实性被保留下来了] 。简单地理解为压缩后的数据还原出原数据的准确度为 99%。另外，常用的比率还有 0.05，这个时候数据还原率就是 95%。在实际应用中，可以根据要解决问题的场景来决定这个比率。

假设我们的还原率要求是 99%，那么用下面的算法来选择参数 k：

1. 让 k=1

2. 运行 PCA 算法，计算出

   $$U_{reduce},Z^{(1)},Z^{(2)},\cdots ,Z^{(m)},x_{approx}^1,x_{approx}^2,\cdots x_{approx}^m$$

3. 利用

   $$\begin{gathered} \frac{ \\ \frac{1}{m}\sum _{i=1}^m||x^{(i)}-x_{approx}^{(i)}|{|}^2 \\ }{ \\ \frac{1}{m}\sum _{i=1}^m||x^{(i)}||} \end{gathered}$$

   计算投射误差率，并判断是否满足要求，如果不满足要求，k=k+1，继续步骤 2;如果满足要求，k 即是我们选择的参数。

这个算法较容易理解，但实际上效率非常低，因为每做一次循环都需要运行一遍 PCA 算法。另一个更高效的方法是，利用协方差矩阵进行奇异值分解返回的 S 矩阵：$ [U,S,V]=svd(\sum)$ 。其中，$S$ 是个 $nxn$ 对角矩阵，即只有对角线上的值非零时其他元素均为 0。

从数学上可以证明，投射误差率也可以使用下面的公式计算：

$$\begin{gathered} 1-\frac{ \\ \sum _{i=1}^k||S_{ii} \\ }{ \\ \sum _{i=1}^n||S_{ii} \\ } \end{gathered}$$

这样运算效率大大提高了，我们只需要进行一次 svd 运算即可。

加快监督机器学习算法的运算速度

PCA 的一个典型应用是用来 加快监督学习的速度 。

例如，我们有 m 个训练数据 (x^(1)^,y^(1)^)，(x^(2)^,y^(2)^),...,(x^(m)^,y^(m)^), 其中，x^(1)^是 10000 维的数据，想像一下，如果这是个图片分类问题，如果输入的图片是 100x100 分辨率的，那么我们就有 10000 维的输入数据。

使用 PCA 来加快算法运算速度时，我们把输入数据分解出来 x^(1)^，x^(2)^，…，x^(m)^，然后运用 PCA 算法对输入数据进行降维压缩，得到降维后的数据 z^(1)^，z^(2)^，…，z^(m)^，最后得到新的训练样例 (z^(1)^，y^(1)^)，(z^(2)^，y^(2)^)，(z^(m)^，y^(m)^)。利用新的训练样例训练出关于压缩后的变量 z 的预测函数 h~θ~(z)。

思考 ：针对图片分类问题，使用 PCA 算法进行数据降维，与直接把图片进行缩放处理相比，有什么异同点？

需要注意，PCA 算法只用来处理训练样例，运行 PCA 算法得到的转换参数 $U_{reduce}$ 可以用来对交叉验证数据集 $x_{cv}^{(i)}$ 及测试数据集 $x_{test}^{(i)}$ 进行转换。当然，还需要相应地对数据进行归一化处理或对数据进行缩放。

实例：人脸识别

查看数据集里所有 400 张照片的缩略图。数据集总共包含 40 位人员的照片，每个人 10 张照片。读者可以在代码里下载数据集，也可以直接使用笔者下载好的数据集。已经下载好的数据集在随书代码目录 datasets/olivetti.pkz 下。

加载数据

下载完照片，就可以使用下面的代码来加载这些照片了：

import numpy as np
from sklearn.datasets import fetch_olivetti_faces

data_home = 'datasets/'
faces = fetch_olivetti_faces(data_home=data_home)

print(faces)

加载的图片数据集保存在 faces 变量里，scikit-learn 已经替我们把每张照片做了初步的处理，剪裁成 64×64 大小且人脸居中显示。这一步至关重要，否则我们的模型将被大量的噪声数据，即图片背景干扰。因为人脸识别的关键是五官纹理和特征，每张照片的背景都不同，人的发型也可能经常变化，这些特征都应该尽量排队在输入特征之外。最后，要成功加载数据集，还需要安装 Python 的图片处理工具包 Pillow，否则无法对图片进行解码，读者可参阅第 2 章开发环境搭建中的内容。

成功加载数据后，其 data 里保存的就是按照 scikit-learn 要求的训练数据集，target 里保存的就是类别目标索引。我们通过下面的代码，将数据集的概要信息显示出来：

# 处理数据
X = faces.data
y = faces.target
targets = np.unique(faces.target)
target_names = np.array(["c%d" % t for t in targets])
n_targets = target_names.shape[0]
n_samples, h, w = faces.images.shape
print('样本图片数量：{}\n特征结果数量：{}'.format(n_samples, n_targets))
print('图片大小：{}x{}\n数据形状：{}\n'.format(w, h, X.shape))

计算机上的输出如下：

样本图片数量: 400
特征结果数量: 40
图片大小: 64x64
数据形状: (400, 4096)

从输出可知，总共有 40 位人物的照片，图片总数是 400 张，输入特征有 4096 个。为了后续区分不同的人物，我们用索引号给目标人物命名，并保存在变量 target_names 里。为了更直观地观察数据，从每个人物的照片里随机选择一张显示出来。先定义一个函数来显示照片阵列：

# 绘制显示图片方法
def plot_gallery(images, titles, h, w, n_row=2, n_col=5):
    """显示图片阵列"""
    plt.figure(figsize=(2 * n_col, 2.2 * n_row), dpi=144)
    plt.subplots_adjust(bottom=0, left=.01, right=.99, top=.90, hspace=.01)
    for i in range(n_row * n_col):
        plt.subplot(n_row, n_col, i + 1)
        plt.imshow(images[i].reshape((h, w)), cmap=plt.cm.gray)
        plt.title(titles[i])
        plt.axis('off')

输入参数 images 是一个二维数据，每一行都是一个图片数据。在加载数据时，fetch_olivetti_faces() 函数已经帮我们做了预处理，图片的每个像素的 RGB 值都转换成了[0，1]的浮点数。因此，我们画出来的照片将是黑白的，而不是彩色的。在图片识别领域，一般情况下用黑白照片就可以了，可以减少计算量，也会让模型更准确。

接着分成两行显示出这些人物的照片：

# 绘制图片
n_row = 2
n_col = 6

sample_images = None
sample_titles = []
for i in range(n_targets):
    people_images = X[y == i]
    people_sample_index = np.random.randint(0, people_images.shape[0], 1)
    people_sample_image = people_images[people_sample_index, :]
    # 拼接特征图片
    if sample_images is not None:
        sample_images = np.concatenate((sample_images, people_sample_image), axis=0)
    else:
        sample_images = people_sample_image
    # 添加特征的标题
    sample_titles.append(target_names[i])

plot_gallery(sample_images, sample_titles, h, w, n_row, n_col)
plt.show()

代码中，X[y==i]可以选择出属于特定人物的所有照片，随机选择出来的照片都放在 sample_images 数组对象里，最后使用我们之前定义的函数 plot_gallery() 把照片画出来

从图片中可以看到，fetch_olivetti_faces() 函数帮我们剪裁了中间部分，只留下脸部特征。

最后，把数据集划分成训练数据集和测试数据集：

# 划分数据集
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=4)

一次失败的尝试

我们使用支持向量机来实现人脸识别

我们指定 SVC 的 class_weight 参数，让 SVC 模型能根据训练样本的数量来均衡地调整权重，这对不均匀的数据集，即目标人物的照片数量相差较大的情况是非常有帮助的。由于总共只有 400 张照片，数据规模较小，模型运行时间不长。

先需要加载数据

import numpy as np
from sklearn.datasets import fetch_olivetti_faces

data_home = 'datasets/'
faces = fetch_olivetti_faces(data_home=data_home)

X = faces.data
y = faces.target
targets = np.unique(faces.target)
target_names = np.array(["c%d" % t for t in targets])
n_targets = target_names.shape[0]

# 划分数据集
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=4)

接着，针对测试数据集进行预测：

from sklearn.svm import SVC

clf = SVC(class_weight='balanced')
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)

最后，分别使用 confusion_matrix 和 classification_report 来查看模型分类的准确性。

from sklearn.metrics import confusion_matrix

# 打印混淆矩阵
cm = confusion_matrix(y_test, y_pred, labels=range(n_targets))
np.set_printoptions(threshold=np.inf)
print("confusion matrix:\n", cm)

# 打印报告信息
from sklearn.metrics import classification_report

print(classification_report(y_test, y_pred))

confusion matrix 理想的输出，是矩阵的对角线上有数字，其他地方都没有数字。但我们的结果显示不是这样的。可以明显看出，很多图片都被预测成索引为 12 的类别了。结果看起来完全不对，这是怎么回事呢？

40 个类别里，查准率、召回率、F1 Score 全为 0，不能有更差的预测结果了。问题是为什么？哪里出了差错？

答案是，我们把每个像素都作为一个输入特征来处理，这样的数据噪声太严重了，模型根本没有办法对训练数据集进行拟合。想想看，我们总共有 4096 个特征，可是数据集大小才 400 个，比特征个数还少，而且我们还需要把数据集分出 20% 来作为测试数据集，这样训练数据集就更小了。这样的状况下，模型根本无法进行准确地训练和预测。

使用 PCA 来处理数据集

解决上述问题的一个办法是使用 PCA 来给数据降维，只选择前 k 个最重要的特征。问题来了，选择多少个特征合适呢？即怎么确定 k 的值？

$$\begin{gathered} \frac{ \\ \frac{1}{m}\sum _{i=1}^m||x^{(i)}-x_{approx}^{(i)}|{|}^2 \\ }{ \\ \frac{1}{m}\sum _{i=1}^m||x^{(i)}||} \end{gathered}$$

在 scikit-learn 里，可以从 PCA 模型的 explained_variance_ratio_变量里获取经 PCA 处理后的数据还原率。这是一个数组，所有元素求和即可知道我们选择的 k 值的数据还原率，数值越大说明失真越小，随着 k 值的增大，数值会无限接近于 1。

利用这一特性，可以让 k 取值 10~300 之间，每隔 30 进行一次取样。在所有的 k 值样本下，计算经过 PCA 算法处理后的数据还原率。然后根据数据还原率要求，来确定合理的 k 值。针对我们的情况，选择失真度小于 5%，即 PCA 处理后能保留 95% 的原数据信息。其代码如下：

from sklearn.decomposition import PCA

"""对数据进行降维"""
candidate_components = range(10, 300, 30)
explained_ratios = []
for c in candidate_components:
    # 设置 n_components 降维
    pca = PCA(n_components=c)
    X_pca = pca.fit_transform(X)
    # 获取数据还原率
    explained_ratios.append(np.sum(pca.explained_variance_ratio_))

# 绘制数据还原率
plt.figure(figsize=(10, 6), dpi=144)
plt.grid()
plt.plot(candidate_components, explained_ratios)
plt.xlabel('Number of PCA Components')
plt.ylabel('Explained Variance Ratio')
plt.title('Explained variance ratio for PCA')
plt.yticks(np.arange(0.5, 1.05, .05))
plt.xticks(np.arange(0, 300, 20))
plt.show()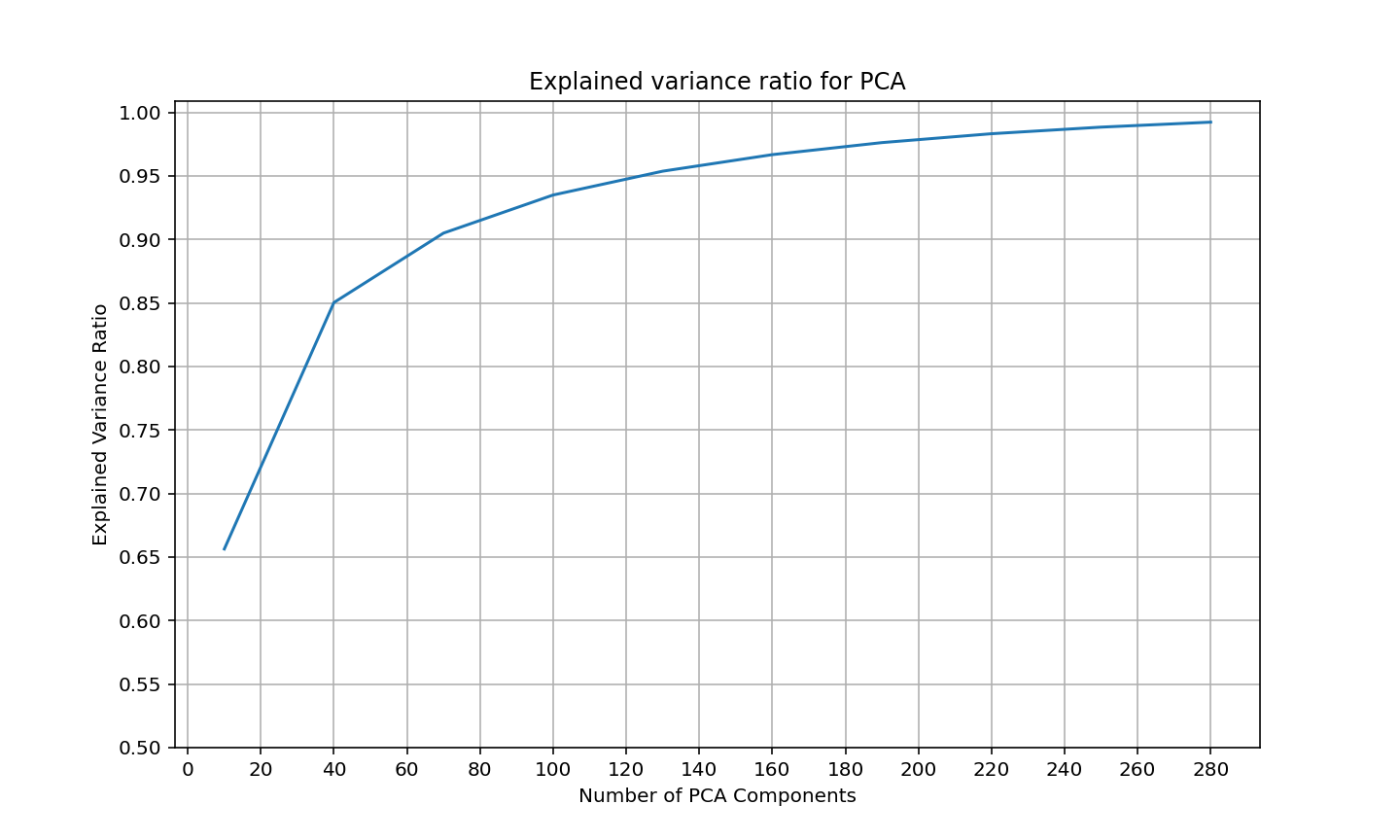

横坐标表示 k 值，纵坐标表示数据还原率。从图中可以看出，要保留 95% 以上的数据还原率，k 值选择 140 即可。也可以非常容易地找出不同的数据还原率所对应的 k 值。为了更直观地观察和对比在不同数据还原率下的数据，我们选择数据还原率分别在 95%、90%、80%、70%、60% 的情况下，画出经 PCA 处理后的图片。从图中不难看出，这些数据还原率对应的 k 值分别是 140、75、37、19、8。

为了方便，这里直接选择画出的人物的前 5 位作为我们的样本图片。每行画出 5 个图片，先画出原图，接着再画出每行在不同数据还原率下对应的图片。

"""绘制出降维图片代码"""


def plot_gallery(images, titles, h, w, n_row=2, n_col=5):
    """显示图片阵列"""
    plt.figure(figsize=(2 * n_col, 2.2 * n_row), dpi=144)
    plt.subplots_adjust(bottom=0, left=.01, right=.99, top=.90, hspace=.01)
    for i in range(n_row * n_col):
        plt.subplot(n_row, n_col, i + 1)
        plt.imshow(images[i].reshape((h, w)), cmap=plt.cm.gray)
        plt.title(titles[i])
        plt.axis('off')


def title_prefix(prefix, title):
    return "{}: {}".format(prefix, title)


sample_images = None
sample_titles = []
for i in range(n_targets):
    people_images = X[y == i]
    people_sample_index = np.random.randint(0, people_images.shape[0], 1)
    people_sample_image = people_images[people_sample_index, :]
    if sample_images is not None:
        sample_images = np.concatenate((sample_images, people_sample_image), axis=0)
    else:
        sample_images = people_sample_image
    sample_titles.append(target_names[i])

n_row = 1
n_col = 5

sample_images = sample_images[0:5]
sample_titles = sample_titles[0:5]

plotting_images = sample_images
plotting_titles = [title_prefix('orig', t) for t in sample_titles]
candidate_components = [140, 75, 37, 19, 8]
for c in candidate_components:
    pca = PCA(n_components=c)
    pca.fit(X)
    X_sample_pca = pca.transform(sample_images)
    X_sample_inv = pca.inverse_transform(X_sample_pca)
    plotting_images = np.concatenate((plotting_images, X_sample_inv), axis=0)
    sample_title_pca = [title_prefix('{}'.format(c), t) for t in sample_titles]
    plotting_titles = np.concatenate((plotting_titles, sample_title_pca), axis=0)

plot_gallery(plotting_images, plotting_titles, h, w,
             n_row * (len(candidate_components) + 1), n_col)

plt.show()

代码里，我们把所有的图片收集进 plotting_images 数组，然后调用前面定义的 plot_gallery() 函数一次性地画出来。

图中第 1 行显示的是原图，第 2 行显示的是数据还原度在 95% 处，即 k=140 的图片；第 2 行显示的是数据还原度在 90% 处，即 k=90 的图片；依此类推。读者可以直观地观察到，原图和 95% 数据还原率的图片没有太大差异。另外，即使在 k=8 时，图片依然能比较清楚地反映出人物的脸部特征轮廓。

最终结果

接下来问题就变得简单了。我们选择 k=140 作为 PCA 参数，对训练数据集和测试数据集进行特征提取。

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=4)

n_components = 140

pca = PCA(n_components=n_components, svd_solver='randomized', whiten=True).fit(X_train)

X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)

接着使用 GridSearchCV 来选择一个最佳的 SVC 模型参数，然后使用最佳参数对模型进行训练。

from sklearn.model_selection import GridSearchCV

param_grid = {'C': [1, 5, 10, 50, 100],
              'gamma': [0.0001, 0.0005, 0.001, 0.005, 0.01]}
clf = GridSearchCV(SVC(kernel='rbf', class_weight='balanced'), param_grid, verbose=2, n_jobs=4)
clf = clf.fit(X_train_pca, y_train)
print(clf.best_params_)

接着使用这一模型对测试样本进行预测，并且使用 confusion_matrix 输出预测准确性信息。

y_pred = clf.best_estimator_.predict(X_test_pca)
cm = confusion_matrix(y_test, y_pred, labels=range(n_targets))

np.set_printoptions(threshold=np.inf)
print(cm)

从输出的对角线上的数据可以看出，大部分预测结果都正确。我们再使用 classification_report 输出分类报告，查看测准率， 召回率及 F1 Score。

print(classification_report(y_test, y_pred))

在总共只有 400 张图片，每位目标人物只有 10 张图片的情况下，精准率和召回率平均达到了 0.95 以上，这是一个非常了不起的性能。