分类评估方法

了解什么是混淆矩阵
知道分类评估中的精确率和召回率
知道 roc 曲线和 auc 指标

分类评估方法

精确率与召回率

混淆矩阵（Confusion Matrix）

在分类任务下，预测结果 (Predicted Condition) 与正确标记 (True Condition) 之间存在四种不同的组合，构成混淆矩阵 ( 适用于多分类)

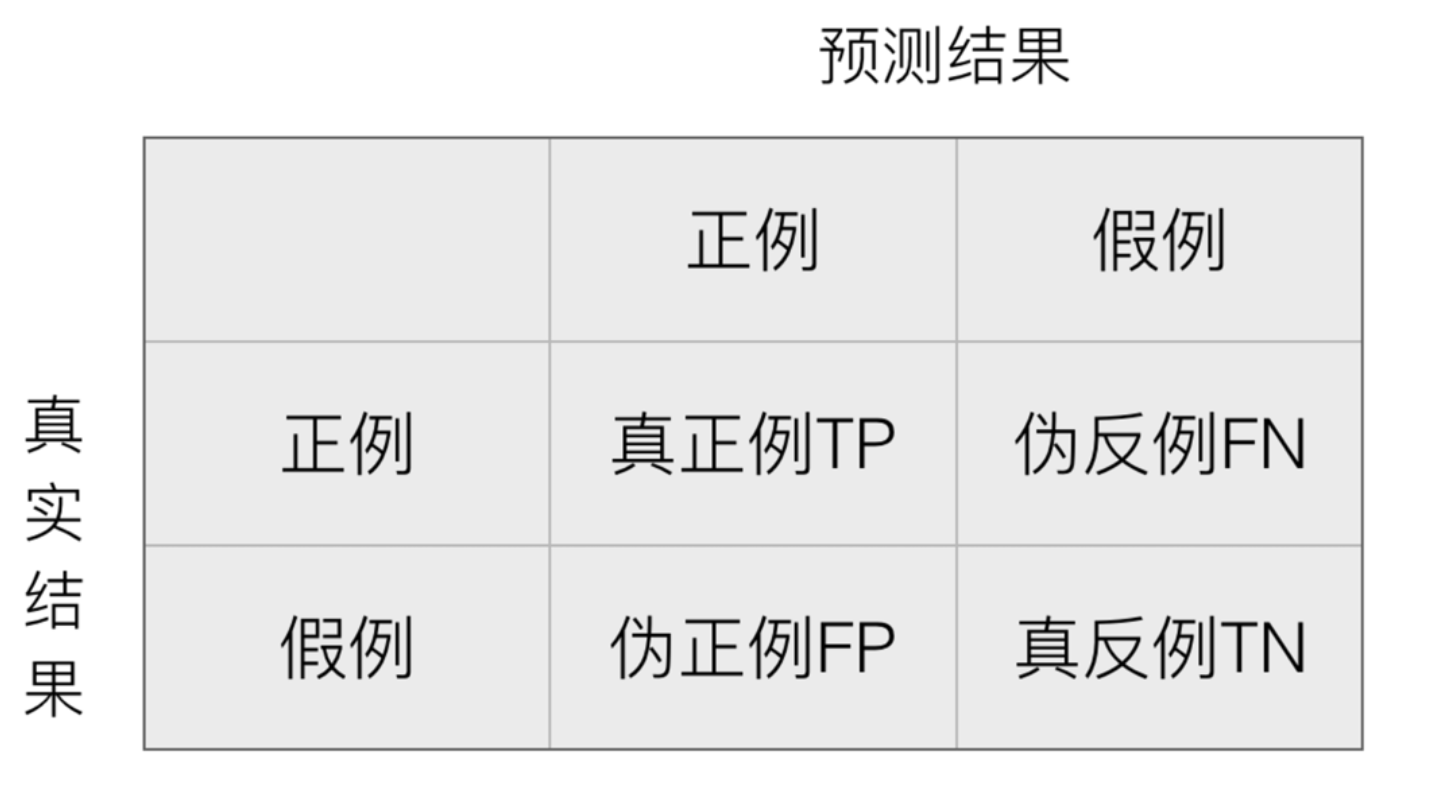
精确率 (Precision) 与召回率 (Recall)

精确率：预测结果为正例样本中真实为正例的比例（了解）

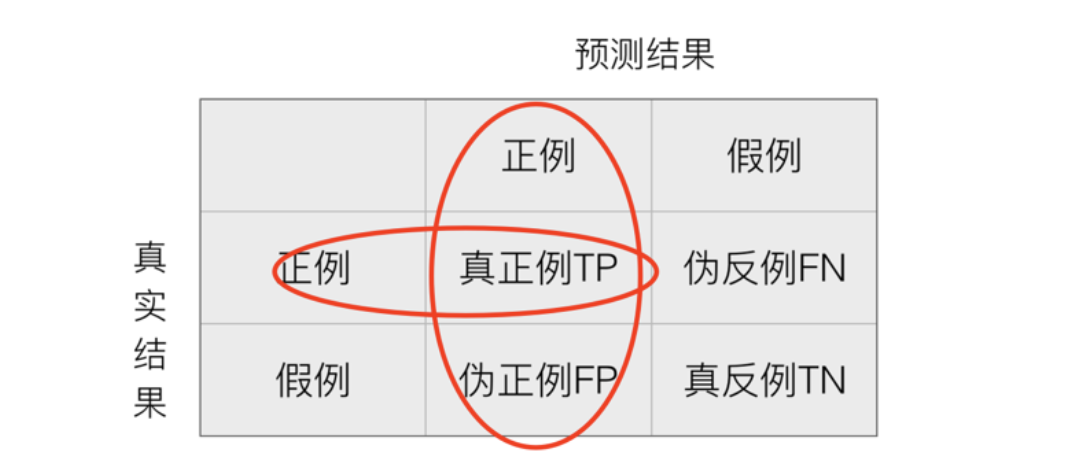
召回率：真实为正例的样本中预测结果为正例的比例（查得全，对正样本的区分能力）

F1-score

还有其他的评估标准，F1-score，反映了模型的稳健型

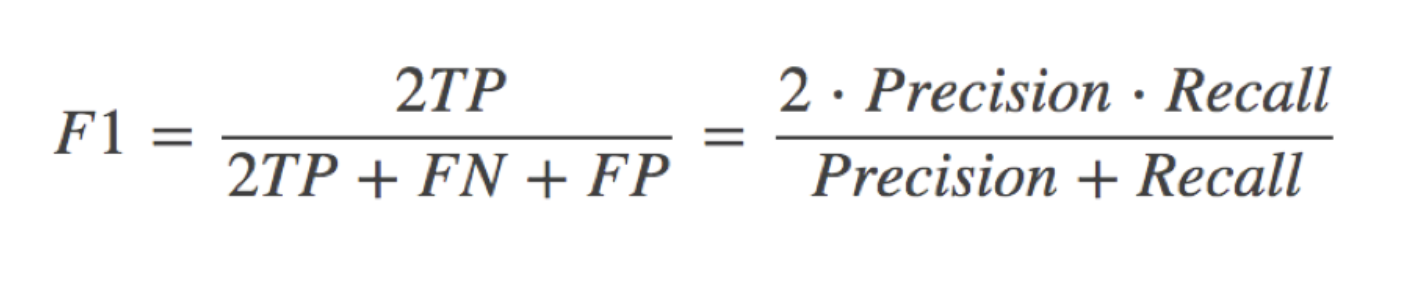
分类评估报告 API

sklearn.metrics.classification_report(y_true, y_pred, labels=[], target_names=None )
- y_true：真实目标值
- y_pred：估计器预测目标值
- labels:指定类别对应的数字
- target_names：目标类别名称
- return：每个类别精确率与召回率

python

ret = classification_report(
  y_test, y_predict, labels=(2, 4), target_names=("良性", "恶性")
)
print(ret)

假设这样一个情况，如果 99 个样本癌症，1 个样本非癌症，不管怎样我全都预测正例 (默认癌症为正例),准确率就为 99% 但是这样效果并不好，这就是样本不均衡下的评估问题

问题：如何衡量样本不均衡下的评估？

ROC 曲线与 AUC 指标

TPR 与 FPR

TPR = TP / (TP + FN)
- 所有真实类别为 1 的样本中，预测类别为 1 的比例
FPR = FP / (FP + TN)
- 所有真实类别为 0 的样本中，预测类别为 1 的比例

ROC 曲线

ROC 曲线的横轴就是 FPRate，纵轴就是 TPRate，当二者相等时，表示的意义则是：对于不论真实类别是 1 还是 0 的样本，分类器预测为 1 的概率是相等的，此时 AUC 为 0.5

ROC

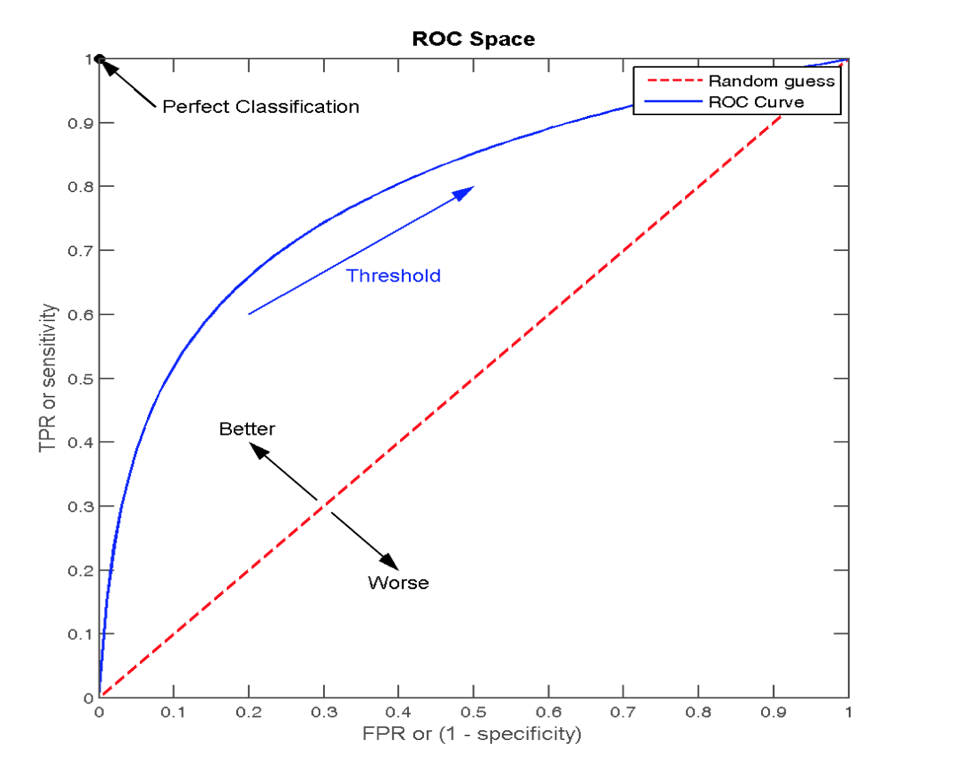
AUC 指标

AUC 的概率意义是随机取一对正负样本，正样本得分大于负样本得分的概率
AUC 的范围在[0, 1]之间，并且越接近 1 越好，越接近 0.5 属于乱猜
AUC=1，完美分类器，采用这个预测模型时，不管设定什么阈值都能得出完美预测。绝大多数预测的场合，不存在完美分类器。
**0.5

AUC 计算 API

from sklearn.metrics import roc_auc_score
- sklearn.metrics.roc_auc_score(y_true, y_score)
  - 计算 ROC 曲线面积，即 AUC 值
  - y_true：每个样本的真实类别，必须为 0(反例),1(正例) 标记
  - y_score：预测得分，可以是正类的估计概率、置信值或者分类器方法的返回值

python

# 0.5~1 之间，越接近于 1 约好
y_test = np.where(y_test > 2.5, 1, 0)

print("AUC 指标：", roc_auc_score(y_test, y_predict)

AUC 只能用来评价二分类
AUC 非常适合评价样本不平衡中的分类器性能

小结

混淆矩阵【了解】
- 真正例（TP）
- 伪反例（FN）
- 伪正例（FP）
- 真反例（TN）
精确率 (Precision) 与召回率 (Recall)【知道】
- 准确率：（对不对）
  - （TP+TN）/(TP+TN+FN+FP)
- 精确率 -- 查的准不准
  - TP/(TP+FP)
- 召回率 -- 查的全不全
  - TP/(TP+FN)
- F1-score
  - 反映模型的稳健性
roc 曲线和 auc 指标【知道】
- roc 曲线
  - 通过 tpr 和 fpr 来进行图形绘制，然后绘制之后，行成一个指标 auc
- auc
  - 越接近 1，效果越好
  - 越接近 0，效果越差
  - 越接近 0.5，效果就是胡说
- 注意：
  - 这个指标主要用于评价不平衡的二分类问题

ROC 曲线的绘制

关于 ROC 曲线的绘制过程，通过以下举例进行说明

假设有 6 次展示记录，有两次被点击了，得到一个展示序列（1:1,2:0,3:1,4:0,5:0,6:0），前面的表示序号，后面的表示点击（1）或没有点击（0）。

然后在这 6 次展示的时候都通过 model 算出了点击的概率序列。

下面看三种情况。

曲线绘制

如果概率的序列是（1:0.9,2:0.7,3:0.8,4:0.6,5:0.5,6:0.4）。

与原来的序列一起，得到序列（从概率从高到低排）

1	1	0	0	0	0
0.9	0.8	0.7	0.6	0.5	0.4

绘制的步骤是：

1）把概率序列从高到低排序，得到顺序（1:0.9,3:0.8,2:0.7,4:0.6,5:0.5,6:0.4）；

2）从概率最大开始取一个点作为正类，取到点 1，计算得到 TPR=0.5，FPR=0.0；

3）从概率最大开始，再取一个点作为正类，取到点 3，计算得到 TPR=1.0，FPR=0.0；

4）再从最大开始取一个点作为正类，取到点 2，计算得到 TPR=1.0，FPR=0.25;

5）以此类推，得到 6 对 TPR 和 FPR。

然后把这 6 对数据组成 6 个点 (0,0.5),(0,1.0),(0.25,1),(0.5,1),(0.75,1),(1.0,1.0)。

这 6 个点在二维坐标系中能绘出来。

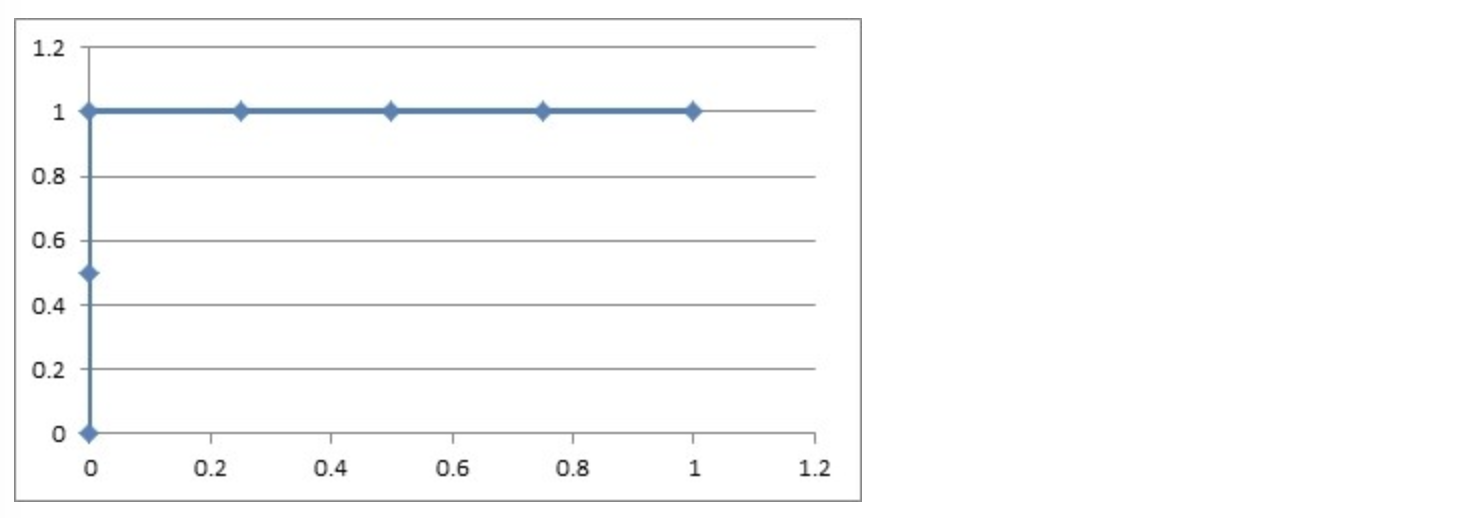
看看图中，那个就是 ROC 曲线。

如果概率的序列是（1:0.9,2:0.8,3:0.7,4:0.6,5:0.5,6:0.4）

与原来的序列一起，得到序列（从概率从高到低排）

1	0	1	0	0	0
0.9	0.8	0.7	0.6	0.5	0.4

绘制的步骤是：

6）把概率序列从高到低排序，得到顺序（1:0.9,2:0.8,3:0.7,4:0.6,5:0.5,6:0.4）；

7）从概率最大开始取一个点作为正类，取到点 1，计算得到 TPR=0.5，FPR=0.0；

8）从概率最大开始，再取一个点作为正类，取到点 2，计算得到 TPR=0.5，FPR=0.25；

9）再从最大开始取一个点作为正类，取到点 3，计算得到 TPR=1.0，FPR=0.25;

10）以此类推，得到 6 对 TPR 和 FPR。

然后把这 6 对数据组成 6 个点 (0,0.5),(0.25,0.5),(0.25,1),(0.5,1),(0.75,1),(1.0,1.0)。

这 6 个点在二维坐标系中能绘出来。

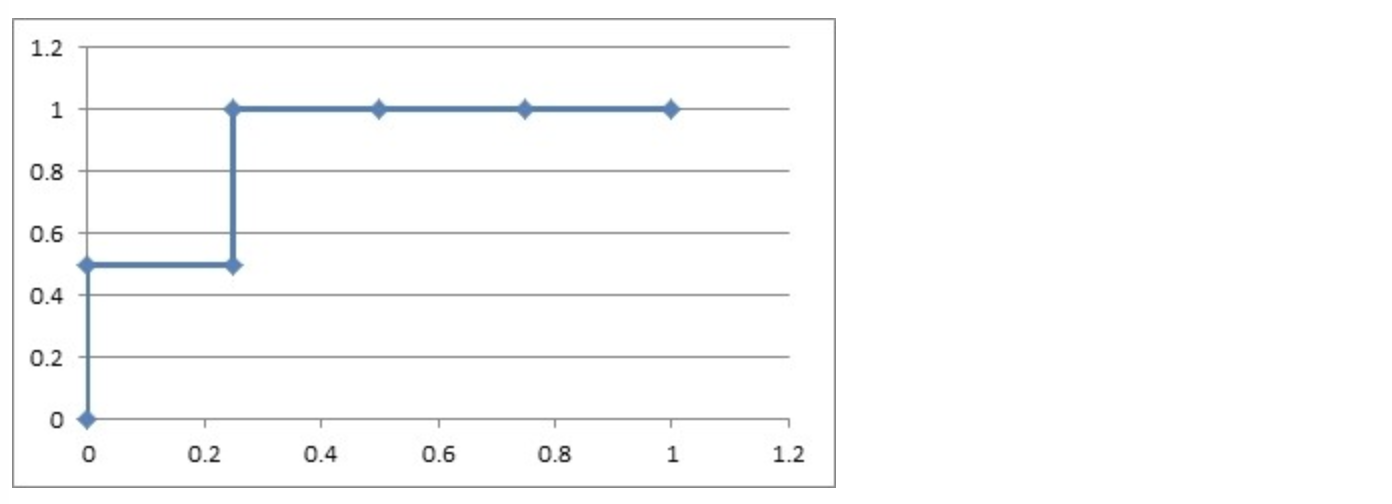
看看图中，那个就是 ROC 曲线。

如果概率的序列是（1:0.4,2:0.6,3:0.5,4:0.7,5:0.8,6:0.9）

与原来的序列一起，得到序列（从概率从高到低排）

0	0	0	0	1	1
0.9	0.8	0.7	0.6	0.5	0.4

绘制的步骤是：

11）把概率序列从高到低排序，得到顺序（6:0.9,5:0.8,4:0.7,2:0.6,3:0.5,1:0.4）；

12）从概率最大开始取一个点作为正类，取到点 6，计算得到 TPR=0.0，FPR=0.25；

13）从概率最大开始，再取一个点作为正类，取到点 5，计算得到 TPR=0.0，FPR=0.5；

14）再从最大开始取一个点作为正类，取到点 4，计算得到 TPR=0.0，FPR=0.75;

15）以此类推，得到 6 对 TPR 和 FPR。

然后把这 6 对数据组成 6 个点 (0.25,0.0),(0.5,0.0),(0.75,0.0),(1.0,0.0),(1.0,0.5),(1.0,1.0)。

这 6 个点在二维坐标系中能绘出来。

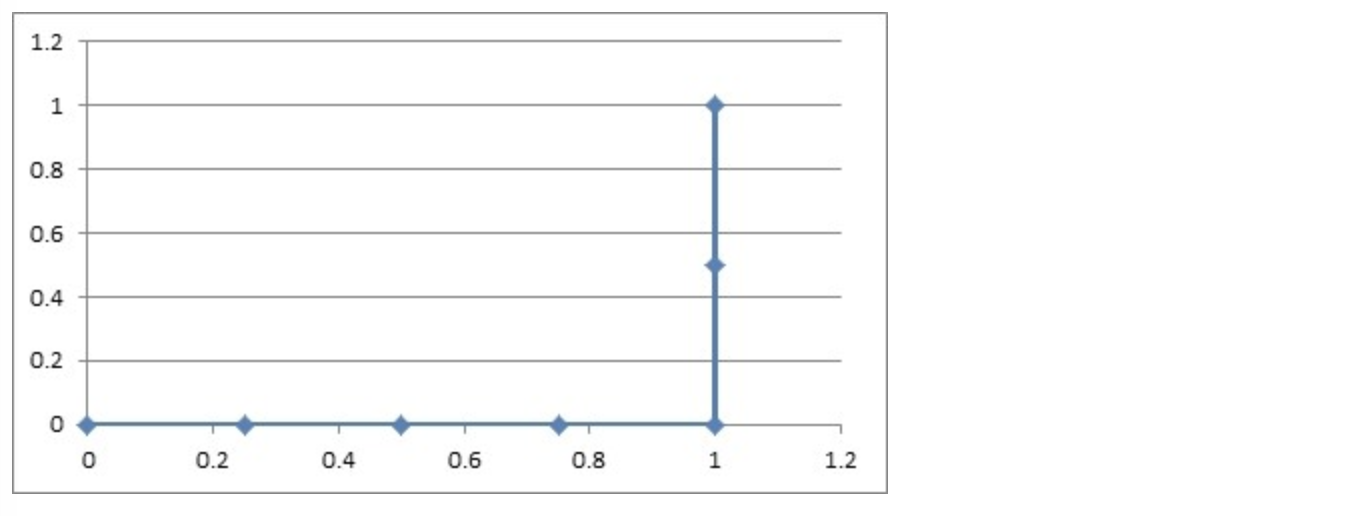
看看图中，那个就是 ROC 曲线。

意义解释

如上图的例子，总共 6 个点，2 个正样本，4 个负样本，取一个正样本和一个负样本的情况总共有 8 种。

上面的第一种情况，从上往下取，无论怎么取，正样本的概率总在负样本之上，所以分对的概率为 1，AUC=1。再看那个 ROC 曲线，它的积分是什么？也是 1，ROC 曲线的积分与 AUC 相等。

上面第二种情况，如果取到了样本 2 和 3，那就分错了，其他情况都分对了；所以分对的概率是 0.875，AUC=0.875。再看那个 ROC 曲线，它的积分也是 0.875，ROC 曲线的积分与 AUC 相等。

上面的第三种情况，无论怎么取，都是分错的，所以分对的概率是 0，AUC=0.0。再看 ROC 曲线，它的积分也是 0.0，ROC 曲线的积分与 AUC 相等。

很牛吧，其实 AUC 的意思是——Area Under roc Curve，就是 ROC 曲线的积分，也是 ROC 曲线下面的面积。

绘制 ROC 曲线的意义很明显，不断地把可能分错的情况扣除掉，从概率最高往下取的点，每有一个是负样本，就会导致分错排在它下面的所有正样本，所以要把它下面的正样本数扣除掉（1-TPR，剩下的正样本的比例）。总的 ROC 曲线绘制出来了，AUC 就定了，分对的概率也能求出来了。

小结

ROC 曲线的绘制【知道】
- 1.构建模型，把模型的概率值从大到小进行排序
- 2.从概率最大的点开始取值，一直进行 tpr 和 fpr 的计算，然后构建整体模型，得到结果
- 3.其实就是在求解积分（面积）

案例

https://www.cnblogs.com/zourui4271/p/10210669.html

https://blog.csdn.net/weixin_41753316/article/details/109382129

分类评估方法 ​