案例改进 - 岭回归
知道岭回归 API 的具体使用
API
python
sklearn.linear_model.Ridge(
alpha=1.0, fit_intercept=True, solver="auto", normalize=False
)- 具有 l2 正则化的线性回归
- alpha:正则化力度,也叫 λ
- λ取值:0~1 1~10
- solver:会根据数据自动选择优化方法
- sag:如果数据集、特征都比较大,选择该随机梯度下降优化
- normalize:数据是否进行标准化
- normalize=False:可以在 fit 之前调用 preprocessing.StandardScaler 标准化数据
- Ridge.coef_:回归权重
- Ridge.intercept_:回归偏置
Ridge 方法相当于 SGDRegressor(penalty='l2', loss="squared_loss"),只不过 SGDRegressor 实现了一个普通的随机梯度下降学习,推荐使用 Ridge(实现了 SAG)
- sklearn.linear_model.RidgeCV(_BaseRidgeCV, RegressorMixin)
- 具有 l2 正则化的线性回归,可以进行交叉验证
- coef_:回归系数
python
class _BaseRidgeCV(LinearModel):
def __init__(self, alphas=(0.1, 1.0, 10.0),
fit_intercept=True, normalize=False, scoring=None,
cv=None, gcv_mode=None,
store_cv_values=False):观察正则化程度的变化,对结果的影响?
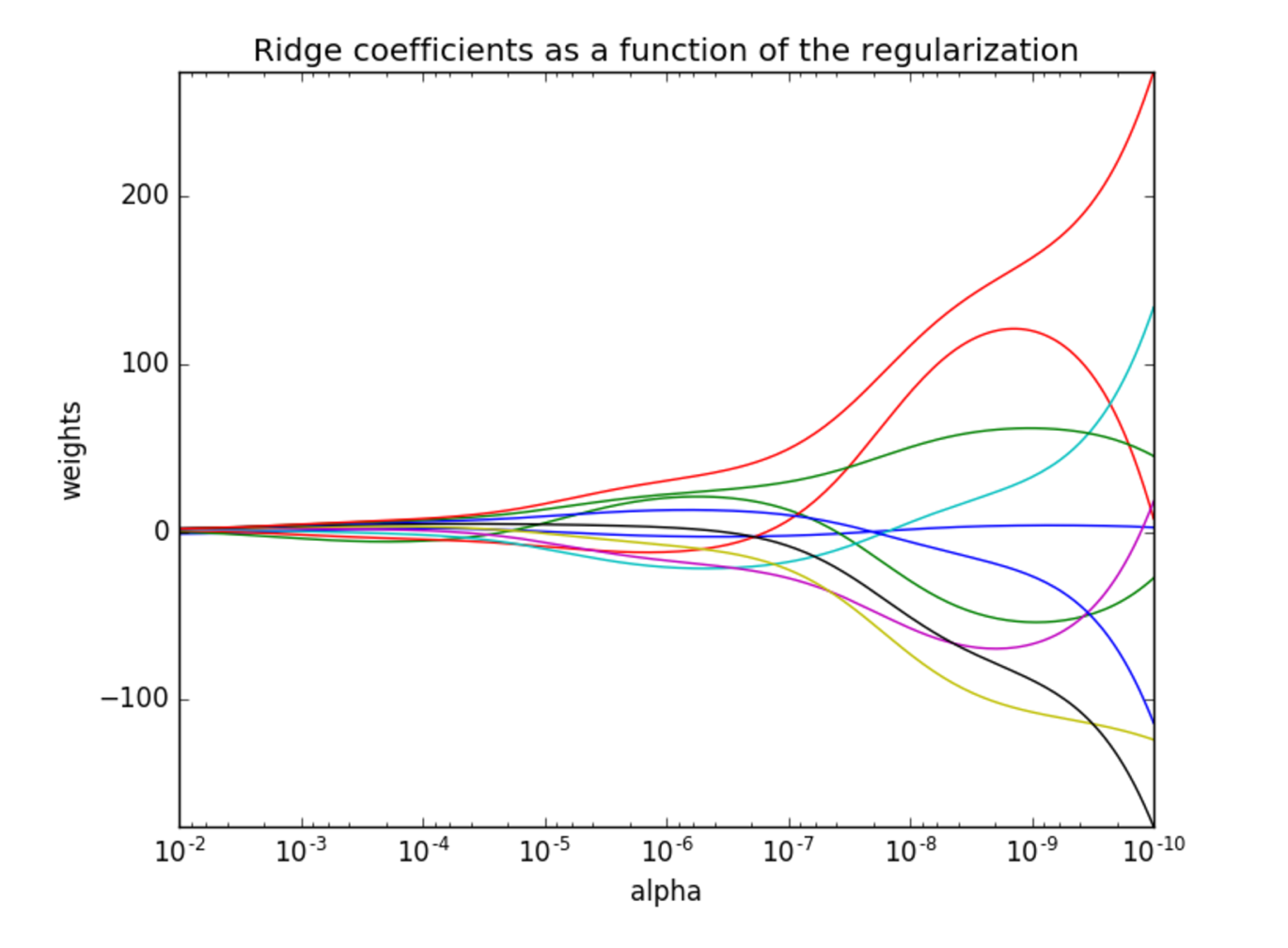
- 正则化力度越大,权重系数会越小
- 正则化力度越小,权重系数会越大
波士顿房价预测
python
from sklearn.datasets import load_boston
from sklearn.linear_model import RidgeCV
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
"""岭回归"""
# 1. 获取数据
boston = load_boston()
# 2. 数据基本处理
# 2.1 数据集划分
x_train, x_test, y_train, y_test = train_test_split(boston.data,
boston.target,
test_size=0.2,
random_state=2)
# 3. 特征工程 --标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)
# 4. 机器学习 (线性回归)
# estimator = Ridge()
# alphas
estimator = RidgeCV(alphas=(0.001, 0.1, 1, 10, 100))
estimator.fit(x_train, y_train)
print("这个模型的偏置是:\n", estimator.intercept_)
# 5. 模型评估
# 5.1 预测值和准确率
y_pre = estimator.predict(x_test)
print("预测值是:\n", y_pre)
score = estimator.score(x_test, y_test)
print("准确率是:\n", score)
# 5.2 均方误差
ret = mean_squared_error(y_test, y_pre)
print("均方误差是:\n", ret)小结
- sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True,solver="auto", normalize=False)【知道】
- 具有 l2 正则化的线性回归
- alpha -- 正则化
- 正则化力度越大,权重系数会越小
- 正则化力度越小,权重系数会越大
- normalize
- 默认封装了,对数据进行标准化处理