PyTorch 使用

一个 Python 深度学习框架，它将数据封装成张量（Tensor）来进行处理。PyTorch 中的张量就是元素为同一种数据类型的多维矩阵。在 PyTorch 中，张量以 "类" 的形式封装起来，对张量的一些运算、处理的方法被封装在类中。

Pytorch 的安装：

pip install torch==2.0.1 -i https://pypi.tuna.tsinghua.edu.cn/simple

张量的创建
张量的类型转换
张量数值计算
张量运算函数
张量索引操作
张量形状操作
张量拼接操作
自动微分模块
案例 - 线性回归案例

张量的基本类型

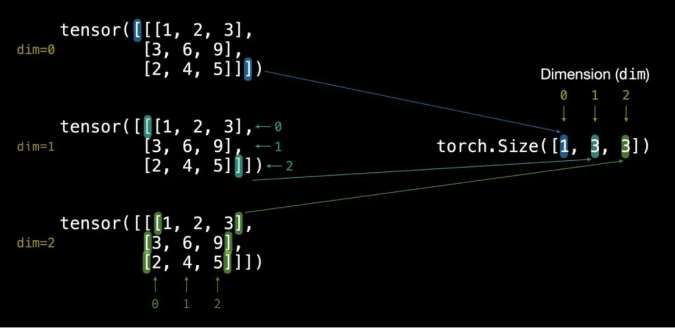
0 维张量：标量 (scalar)

scalar = torch.tensor(7)
scalar.ndim
>>> 0

1 维张量：向量 (vector)

vector = torch.tensor([7, 7])
vector.ndim
>>> 1

2 维张量：矩阵 (matrix)

MATRIX = torch.tensor([[7, 8],
					   [9, 10]])
MATRIX.ndim
>>> 2

多维张量

TENSOR = torch.tensor([[[1, 2, 3],
                        [3, 6, 9],
                        [2, 4, 5]]])
TENSOR.ndim
>>> 3

python

[[[1, 2, 3, 4],
  [3, 6, 9, 7],
  [2, 4, 5, 6]],
 [[1, 2, 3, 6],
  [3, 6, 9, 5],
  [2, 4, 5, 7]]]

# torch.Size(2,3,4)

张量的创建

基本创建方式

torch.tensor 根据指定数据创建张量
torch.Tensor 根据形状创建张量，其也可用来创建指定数据的张量
torch.IntTensor、torch.FloatTensor、torch.DoubleTensor 创建指定类型的张量

1、torch.tensor() 根据指定数据创建张量

python

import torch
import numpy as np

# 1. 创建张量标量
data = torch.tensor(10)
print(data)
# 2. numpy 数组，由于 data 为 float64, 下面代码也使用该类型
data = np.random.randn(2, 3)
data = torch.tensor(data)
print(data)
# 3. 列表，下面代码使用默认元素类型  float32
data = [[10., 20., 30.], [40., 50., 60.]]
data = torch.tensor(data)
print(data)

输出结果 :

tensor(10)
tensor([
    [0.1345, 0.1149, 0.2435],
    [0.8026, -0.6744, -1.0918]], dtype=torch.float64)
tensor([[10., 20., 30.],
    [40., 50., 60.]])

2、torch.Tensor() 根据指定形状创建张量，也可以用来创建指定数据的张量

python

import torch

# 1. 创建 2 行 3 列的张量，默认  dtype 为  float32
data = torch.Tensor(2, 3)
print(data)
# 2. 注意 : 如果传递列表，则创建包含指定元素的张量
data = torch.Tensor([10])
print(data)
data = torch.Tensor([10, 20])
print(data)

输出结果：

tensor([[0.0000e+00, 3.6893e+19, 2.2018e+05],

[4.6577e-10, 2.4158e-12, 1.1625e+33]]) tensor([10.])

tensor([10., 20.])

3、torch.IntTensor()、torch.FloatTensor()、torch.DoubleTensor() 创建指定类型的张量

# 1. 创建2行3列, dtype 为 int32 的张量
data = torch.IntTensor(2, 3)
print(data)
# 2. 注意: 如果传递的元素类型不正确, 则会进行类型转换
data = torch.IntTensor([2.5, 3.3])
print(data)
# 3. 其他的类型
data = torch.ShortTensor() # int16
data = torch.LongTensor() # int64
data = torch.FloatTensor() # float32
data = torch.DoubleTensor() # float64

输出结果

输出结果:
tensor([[ 0, 1610612736, 1213662609],
[ 805308409, 156041223, 1]],
dtype=torch.int32)
tensor([2, 3], dtype=torch.int32)

创建线性和随机张量

torch.arange 和 torch.linspace 创建线性张量
torch.random.init_seed 和 torch.random.manual_seed 随机种子设置
torch.randn 创建随机张量

1、torch.arange()、torch.linspace() 创建线性张量

python

# 1. 在指定区间按照步长生成元素  [start, end, step)
data = torch.arange(0, 10, 2)
print(data)

# 2. 在指定区间按照元素个数生成  [start, end, num]
data = torch.linspace(0, 11, 10)
print(data)

输出结果：

tensor([0, 2, 4, 6, 8])

tensor([ 0.0000, 1.2222, 2.4444, 3.6667, 4.8889, 6.1111, 7.3333, 8.5556, 9.7778, 11.0000])

2、torch.random.initial_seed()、torch.random.manual_seed() 随机数种子设置，torch.randn() 创建随机张量

# 1. 创建随机张量
data = torch.randn(2, 3) # 创建2行3列张量
print(data)
# 查看随机数种子
print('随机数种子:', torch.random.initial_seed())
# 2. 随机数种子设置
torch.random.manual_seed(100)
data = torch.randn(2, 3)
print(data)
print('随机数种子:', torch.random.initial_seed())

输出结果

输出结果:
tensor([[-0.5209, -0.2439, -1.1780],[ 0.8133, 1.1442, 0.6790]])
随机数种子: 4508475192273306739
tensor([[ 0.3607, -0.2859, -0.3938],[ 0.2429, -1.3833, -2.3134]])
随机数种子: 100

3、torch.randn() 创建随机张量

python

# 1. 创建随机张量
data = torch.randn(2, 3)  # 创建 2 行 3 列张量
print(data)

输出结果：

tensor([[-0.5209, -0.2439, -1.1780], [ 0.8133, 1.1442, 0.6790]])

创建 0-1 张量

torch.ones 创建全 1 张量
torch.zeros 创建全 0 张量
torch.full 和 torch.full_like 创建全为指定值张量

1、torch.zeros() 创建全 0 张量

python

# 1. 创建指定形状全 0 张量
data = torch.zeros(2, 3)
print(data)
# 2. 根据张量形状创建全 0 张量
data = torch.zeros_like(data)
print(data)

输出结果：

tensor([[0., 0., 0.], [0., 0., 0.]])
tensor([[0., 0., 0.], [0., 0., 0.]])

2、torch.ones() 创建全 1 张量

python

# 1. 创建指定形状全 1 张量
data = torch.ones(2, 3)
print(data)
# 2. 根据张量形状创建全 1 张量
data = torch.ones_like(data)
print(data)

输出结果：

tensor([[1., 1., 1.], [1., 1., 1.]])
tensor([[1., 1., 1.], [1., 1., 1.]])

3、torch.full() 创建全为指定值张量

python

# 1. 创建指定形状指定值的张量
data = torch.full([2, 3], 10)
print(data)

# 2. 根据张量形状创建指定值的张量
data = torch.full_like(data, 20)
print(data)

输出结果：

tensor([[10, 10, 10], [10, 10, 10]])
tensor([[20, 20, 20], [20, 20, 20]])

张量的类型转换

data.type(torch.DoubleTensor)
data.double()

1, data.type(torch.DoubleTensor)

python

data = torch.full([2, 3], 10)
print(data.dtype)
# 将  data 元素类型转换为  float64 类型
data = data.type(torch.DoubleTensor)
print(data.dtype)
# 转换为其他类型
# data = data.type(torch.ShortTensor)
# data = data.type(torch.IntTensor)
# data = data.type(torch.LongTensor)
# data = data.type(torch.FloatTensor)

输出结果：

torch.int64
torch.float64

2, data.double()

python

data = torch.full([2, 3], 10)
print(data.dtype)
# 将  data 元素类型转换为  float64 类型
data = data.double()
print(data.dtype)
# 转换为其他类型
# data = data.short()
# data = data.int()
# data = data.long()
# data = data.float()

输出结果：

torch.int64
torch.float64

总结

创建张量的方式
- torch.tensor() 根据指定数据创建张量
- torch.Tensor() 根据形状创建张量，其也可用来创建指定数据的张量
- torch.IntTensor()、torch.FloatTensor()、torch.DoubleTensor() 创建指定类型的张量
创建线性和随机张量
- torch.arrange() 和 torch.linspace() 创建线性张量
- torch.random.initial_seed() 和 torch.random.manual_seed() 随机种子设置
- torch.randn() 创建随机张量
创建 01 张量
- torch.ones() 和 torch.ones_like() 创建全 1 张量
- torch.zeros() 和 torch.zeros_like() 创建全 0 张量
- torch.full() 和 torch.full_like() 创建全为指定值张量
张量元素类型转换
- data.type(torch.DoubleTensor)
- data.double()

张量的类型转换

掌握张量转换为 Numpy 数组的方法

掌握 Numpy 数组转换为张量的方法
掌握标量张量和数字转换方法

张量转换为 NumPy 数组

使用 Tensor.numpy 函数可以将张量转换为 ndarray 数组，但是共享内存，可以使用 copy 函数避免共享。

python

# 1. 将张量转换为  numpy 数组
data_tensor = torch.tensor([2, 3, 4])
# 使用张量对象中的 numpy 函数进行转换
data_numpy = data_tensor.numpy()
print(type(data_tensor))
print(type(data_numpy))

# 注意：data_tensor 和 data_numpy 共享内存
# 修改其中的一个，另外一个也会发生改变
# data_tensor[0] = 100
data_numpy[0] = 100
print(data_tensor)
print(data_numpy)

输出结果：

<class 'torch.Tensor'>
<class 'numpy.ndarray'>
tensor([100, 3, 4])
[100 3 4]

使用 Tensor.numpy() 函数可以将张量转换为 ndarray 数组，但是共享内存，可以使用 copy() 函数避免共享

# 2. 对象拷贝避免共享内存
data_tensor = torch.tensor([2, 3, 4])
# 使用张量对象中的 numpy 函数进行转换，通过copy方法拷贝对象
data_numpy = data_tensor.numpy().copy()
print(type(data_tensor))
print(type(data_numpy))
# 注意: data_tensor 和 data_numpy 此时不共享内存
# 修改其中的一个，另外一个不会发生改变
# data_tensor[0] = 100
data_numpy[0] = 100
print(data_tensor)
print(data_numpy)

输出结果：

<class 'torch.Tensor'>
<class 'numpy.ndarray'>
tensor([2, 3, 4])
[100 3 4]

NumPy 数组转换为张量

使用 from_numpy 可以将 ndarray 数组转换为 Tensor。默认共享内存，使用 copy 函数避免共享。
使用 torch.tensor 可以将 ndarray 数组转换为 Tensor。I NumPy 数组转换为张量

1、使用 from_numpy() 可以将 ndarray 数组转换为 Tensor

python

data_numpy = np.array([2, 3, 4])
# 将 numpy 数组转换为张量类型 # 1. from_numpy
# 2. torch.tensor(ndarray)
data_tensor = torch.from_numpy(data_numpy)
# nunpy 和 tensor 共享内存
# data_numpy[0] = 100
print(data_tensor)
print(data_numpy)

输出结果：

tensor([100, 3, 4], dtype=torch.int32)
[100 3 4]

2、使用 torch.tensor() 可以将 ndarray 数组转换为 Tensor。

python

data_numpy = np.array([2, 3, 4])
data_tensor = torch.tensor(data_numpy)
# nunpy 和 tensor 不共享内存
print(data_tensor)
print(data_numpy)

输出结果：

tensor([100, 3, 4], dtype=torch.int32)
[2 3 4]

标量张量和数字转换

对于只有一个元素的张量，使用 item() 函数将该值从张量中提取出来

python

# 当张量只包含一个元素时，可以通过  item() 函数提取出该值
data = torch.tensor([30, ])
print(data.item())
data = torch.tensor(30)
print(data.item())

输出结果：

30
30

总结

张量转换为 numpy 数组
- data_tensor.numpy()
- data_tensor.numpy().copy()
numpy 转换为张量
- torch.from_numpy(data_numpy)
- torch.tensor(data_numpy)
标量张量和数字转换
- data.item()

张量数值计算

张量基本运算

加减乘除取负号：

add、sub、 mul、div、 neg

add_、sub_、mul_、div_、neg_（其中带下划线的版本会修改原数据）

python

data = torch.randint(0, 10, [2, 3])
print(data)
# 1. 不修改原数据
new_data = data.add(10)  # 等价  new_data = data + 10
print(new_data)
# 2. 直接修改原数据  注意 : 带下划线的函数为修改原数据本身 data.add_ (10)  # 等价  data += 10
print(data)
# 3. 其他函数
print(data.sub(100))
print(data.mul(100))
print(data.div(100))
print(data.neg())

输出结果：

tensor([[3, 7, 4],
	[0, 0, 6]])
tensor([[13, 17, 14],
	[10, 10, 16]])
tensor([[13, 17, 14],
	[10, 10, 16]])
tensor([[-87, -83, -86],
	[-90, -90, -84]])
tensor([[1300, 1700, 1400],
	[1000, 1000, 1600]])
tensor([[0.1300, 0.1700, 0.1400],
	[0.1000, 0.1000, 0.1600]])
tensor([[-13, -17, -14],
	[-10, -10, -16]])

点乘运算

点乘指（Hadamard）的是两个同维数组对应位置的元素相乘，使用 mul 和运算符 * 实现。

例如

A = [\begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix}], B = [\begin{matrix} 5 & 6 \\ 7 & 8 \end{matrix}]

则 A,B 的 Hadamard 积：

A ⊙ B = [\begin{matrix} 1 \times 5 & 2 \times 6 \\ 3 \times 7 & 4 \times 8 \end{matrix}] = [\begin{matrix} 5 & 12 \\ 21 & 32 \end{matrix}]

点乘运算

python

data1 = torch.tensor([[1, 2], [3, 4]])
data2 = torch.tensor([[5, 6], [7, 8]])
# 第一种方式
data = torch.mul(data1, data2)
print(data)
# 第二种方式
data = data1 * data2
print(data)

输出结果：

tensor([[5, 12], [21, 32]])
tensor([[5, 12], [21, 32]])

数组乘法运算要求第一个数组 shape: (n, m) ，第二个数组 shape: (m, p), 两个数组乘法运算 shape 为: (n, p)。

运算符 @ 用于进行两个矩阵的乘积运算
torch.matmul 对进行乘积运算的两矩阵形状没有限定。对数输入的 shape 不同的张量，对应的最后几个维度必须符合矩阵运算规则

python

# 乘法运算
data1 = torch.tensor([[1, 2], [3, 4], [5, 6]])
data2 = torch.tensor([[5, 6], [7, 8]])
# 方式一 :
data3 = data1 @ data2
print("data3-->", data3)
# 方式二 :
data4 = torch.matmul(data1, data2)
print("data4-->", data4)

输出结果

data3--> tensor([[19, 22],
	[43, 50],
	[67, 78]])
data4--> tensor([[19, 22],
	[43, 50],
	[67, 78]])

总结

张量基本运算函数
• add、sub、mul、div、neg 等函数
• add_、sub_、mul_、div_、neg_等函数
张量的点乘运算
• mul 和运算符*
矩阵乘法运算
• 运算符@用于进行两个矩阵的乘法运算
• torch.matmul 对应的维度必须符合矩阵运算规则

张量运算函数

PyTorch 为每个张量封装很多实用的计算函数：

均值
平方根
求和
指数计算
对数计算等等

常见运算函数

python

import torch

data = torch.randint(0, 10, [2, 3], dtype=torch.float64)
print(data)
# 1. 计算均值
# 注意 : tensor 必须为  Float 或者  Double 类型
print(data.mean())
print(data.mean(dim=0))  # 按列计算均值
print(data.mean(dim=1))  # 按行计算均值
# 2. 计算总和
print(data.sum())
print(data.sum(dim=0))
print(data.sum(dim=1))
# 3. 计算平方
print(torch.pow(data, 2))

输出结果：

tensor([[4., 0., 7.],
	[6., 3., 5.]], dtype=torch.float64)

tensor(4.1667, dtype=torch.float64)
tensor([5.0000, 1.5000, 6.0000], dtype=torch.float64)
tensor([3.6667, 4.6667], dtype=torch.float64)

tensor(25., dtype=torch.float64)
tensor([10., 3., 12.], dtype=torch.float64)
tensor([11., 14.], dtype=torch.float64)

tensor([[16., 0., 49.],
	[36., 9., 25.]], dtype=torch.float64)

常见运算函数

python

# 4. 计算平方根
print(data.sqrt())

# 5. 指数计算，e^n 次方
print(data.exp())

# 6. 对数计算
print(data.log())  # 以  e 为底
print(data.log2())
print(data.log10())

输出结果：

tensor([[2.0000, 0.0000, 2.6458],[2.4495, 1.7321, 2.2361]],dtype=torch.float64)

tensor([[5.4598e+01, 1.0000e+00, 1.0966e+03],
    [4.0343e+02, 2.0086e+01, 1.4841e+02]], dtype=torch.float64)

tensor([[1.3863, -inf, 1.9459],
    [1.7918, 1.0986, 1.6094]],dtype=torch.float64)
tensor([[2.0000, -inf, 2.8074],
    [2.5850, 1.5850, 2.3219]],dtype=torch.float64)
tensor([[0.6021, -inf, 0.8451],
    [0.7782, 0.4771, 0.6990]],dtype=torch.float64)

张量索引操作

在操作张量时，经常需要去获取某些元素就进行处理或者修改操作，我们需要了解在 torch 中的索引操作。准备数据：

python

import torch  # 随机生成数据

data = torch.randint(0, 10, [4, 5])
print(data)

输出结果：

tensor([[0, 7, 6, 5, 9],
    [6, 8, 3, 1, 0],
    [6, 3, 8, 7, 3],
    [4, 9, 5, 3, 1]])

简单行、列索引

python

print(data[0])
print(data[:, 0])

输出结果：

tensor([0, 7, 6, 5, 9])
tensor([0, 6, 6, 4])

列表索引

python

# 返回  (0, 1)、 (1, 2) 两个位置的元素
print(data[[0, 1], [1, 2]])

# 返回  0、1 行的  1、2 列共 4 个元素
print(data[[[0], [1]], [1, 2]])

输出结果：

python

tensor([7, 3])
tensor([[7, 6], [8, 3]])

范围索引

python

# 前 3 行的前 2 列数据
print(data[:3, :2])

# 第 2 行到最后的前 2 列数据
print(data[2:, :2])

输出结果：

tensor([[0, 7],
[6, 8],
[6, 3]])

tensor([[6, 3], [4, 9]])

布尔索引

python

# 第三列大于 5 的行数据
print(data[data[:, 2] > 5])
# 第二行大于 5 的列数据
print(data[:, data[1] > 5])

输出结果

tensor([[0, 7, 6, 5, 9],
    [6, 3, 8, 7, 3]])
tensor([[0, 7],
    [6, 8],
    [6, 3],
    [4, 9]])

多维索引

python

data = torch.randint(0, 10, [3, 4, 5])
print(data)
# 获取 0 轴上的第一个数据
print(data[0, :, :])
# 获取 1 轴上的第一个数据
print(data[:, 0, :])
# 获取 2 轴上的第一个数据
print(data[:, :, 0])

输出结果：

tensor([[[2, 4, 1, 2, 3],
    [5, 5, 1, 5, 0],
    [1, 4, 5, 3, 8],
    [7, 1, 1, 9, 9]],

    [[9, 7, 5, 3, 1],
    [8, 8, 6, 0, 1],
    [6, 9, 0, 2, 1],
    [9, 7, 0, 4, 0]],

    [[0, 7, 3, 5, 6],
    [2, 4, 6, 4, 3],
    [2, 0, 3, 7, 9],
    [9, 6, 4, 4, 4]]])

tensor([[2, 4, 1, 2, 3],
    [5, 5, 1, 5, 0],
    [1, 4, 5, 3, 8],
    [7, 1, 1, 9, 9]])

tensor([[2, 4, 1, 2, 3],
    [9, 7, 5, 3, 1],
    [0, 7, 3, 5, 6]])

tensor([[2, 5, 1, 7],
    [9, 8, 6, 9],
    [0, 2, 2, 9]])

张量形状操作

掌握 reshape() 、squeeze()、unsqueeze()、transpose()、permute()、view()、contiguous() 等函数使用

reshape() 函数

reshape 函数可以在保证张量数据不变的前提下改变数据的维度，将其转换成指定的形状。

import torch


data = torch.tensor([[10, 20, 30], [40, 50, 60]])
# 1. 使用  shape 属性或者  size 方法都可以获得张量的形状
print(data.shape) print(data.size)

# 2. 使用  reshape 函数修改张量形状
new_data = data.reshape(1, 6) print(new_data.shape)

squeeze() 和 unsqueeze() 函数

squeeze 函数删除形状为 1 的维度（降维），unsqueeze 函数添加形状为 1 的维度（升维）。

python

mydata1 = torch.tensor([1, 2, 3, 4, 5])
print('mydata1--->', mydata1.shape, mydata1)  # 一个普通的数  组  1 维数据
mydata2 = mydata1.unsqueeze(dim=0)
print('在 0 维度上 拓展维度： ', mydata2, mydata2.shape)  # 1*5
mydata3 = mydata1.unsqueeze(dim=1)
print('在 1 维度上 拓展维度： ', mydata3, mydata3.shape)  # 5*1
mydata4 = mydata1.unsqueeze(dim=-1)
print('在 -1 维度上 拓展维度： ', mydata4, mydata4.shape)  # 5*1 mydata5 = mydata4.squeeze()
print('压缩维度： ', mydata5, mydata5.shape)  # 1*5

transpose() 和 permute() 函数

transpose 函数可以实现交换张量形状的指定维度, 例如: 一个张量的形状为 (2, 3, 4) 可以通过 transpose 函数把 3 和 4 进行交换，将张量的形状变为 (2, 4, 3) 。permute 函数可以一次交换更多的维度。

python

data = torch.tensor(np.random.randint(0, 10, [3, 4, 5]))
print('data shape:', data.size())
# 1 交换 1 和 2 维度
mydata2 = torch.transpose(data, 1, 2)
print('mydata2.shape--->', mydata2.shape)
# 2 将 data 的形状修改为  (4, 5, 3), 需要变换多次
mydata3 = torch.transpose(data, 0, 1)
mydata4 = torch.transpose(mydata3, 1, 2)
print('mydata4.shape--->', mydata4.shape)
# 3 使用  permute 函数将形状修改为  (4, 5, 3) # 3-1 方法 1
mydata5 = torch.permute(data, [1, 2, 0])
print('mydata5.shape--->', mydata5.shape)
# 3-2 方法 2
mydata6 = data.permute([1, 2, 0])
print('mydata6.shape--->', mydata6.shape)

view() 和 contiguous() 函数

view 函数也可以用于修改张量的形状，只能用于存储在整块内存中的张量。在 PyTorch 中，有些张量是由不同的数据块组成的，它们并没有存储在整块的内存中，view 函数无法对这样的张量进行变形处理。

python

# 1 若要使用 view 函数，需要使用 contiguous() 变成连续以后再使用 view 函数 # 2 判断张量是否使用整块内存
data = torch.tensor([[10, 20, 30], [40, 50, 60]])
print('data--->', data, data.shape)
# 1 判断是否使用整块内存
print(data.is_contiguous())  # True # 2 view
mydata2 = data.view(3, 2)
print('mydata2--->', mydata2, mydata2.shape)

总结

reshape 函数可以在保证张量数据不变的前提下改变数据的维度
squeeze 和 unsqueeze 函数可以用来增加或者减少维度
transpose 函数可以实现交换张量形状的指定维度，permute 可以一次交换更多的维度
view 函数也可以用于修改张量的形状，但是它要求被转

换的张量内存必须连续，所以一般配合 contiguous 函数使用

张量拼接操作

学习目标

掌握 torch.cat() 使用

• torch.cat() 函数可以将两个张量根据指定的维度拼接起来，不改变维度数。

python

import torch

data1 = torch.randint(0, 10, [1, 2, 3])
data2 = torch.randint(0, 10, [1, 2, 3])
# 1. 按 0 维度拼接
new_data = torch.cat([data1, data2], dim=0)
print(new_data.shape)
# 2. 按 1 维度拼接
new_data = torch.cat([data1, data2], dim=1)
print(new_data.shape)
# 3. 按 2 维度拼接
new_data = torch.cat([data1, data2], dim=2)
print(new_data.shape)

总结

cat() 函数可以将张量按照指定的维度拼接起来

自动微分模块

训练神经网络时，最常用的算法就是反向传播。在该算法中，参数（模型权重）会根据损失函数关于对应参数的梯度进行调整。为了计算这些梯度，PyTorch 内置了名为 torch.autograd 的微分引擎。它支持任意计算图的自动梯度计算：

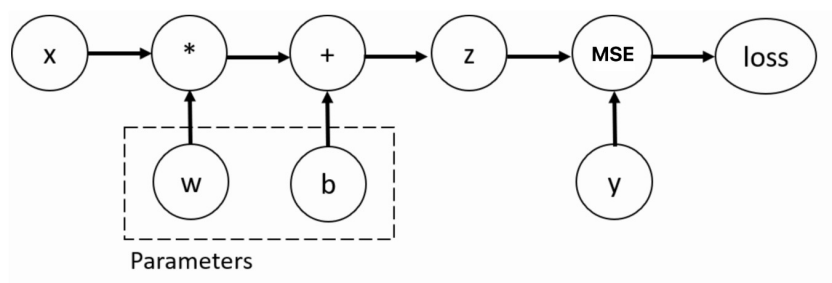
接下来我们使用这个结构进行自动微分模块的介绍。我们使用 backward 方法、grad 属性来实现梯度的计算和访问。

python

import torch


# 1. 当 X 为标量时梯度的计算
def test01():
    x = torch.tensor(5)
    #  目标值
    y = torch.tensor(0.)
    # 设置要更新的权重和偏置的初始值
    w = torch.tensor(1., requires_grad=True, dtype=torch.float32)
    b = torch.tensor(3., requires_grad=True, dtype=torch.float32)
    # 设置网络的输出值
    z = x * w + b  # 矩阵乘法
    # 设置损失函数，并进行损失的计算
    loss = torch.nn.MSELoss()
    loss = loss(z, y)
    # 自动微分
    loss.backward()
    # 打印 w,b 变量的梯度
    # backward 函数计算的梯度值会存储在张量的 grad 变量中 print("W 的梯度:", w.grad)
    print("b 的梯度", b.grad)

输出结果：

# 当 X 是标量时的结果 W 的梯度：tensor(80.) b 的梯度 tensor(16.)

python

import torch


def test02():
    # 输入张量 2*5
    x = torch.ones(2, 5)
    #  目标值是 2*3
    y = torch.zeros(2, 3)
    # 设置要更新的权重和偏置的初始值
    w = torch.randn(5, 3, requires_grad=True)
    b = torch.randn(3, requires_grad=True)
    # 设置网络的输出值
    z = torch.matmul(x, w) + b  # 矩阵乘法
    # 设置损失函数，并进行损失的计算
    loss = torch.nn.MSELoss()
    loss = loss(z, y)
    # 自动微分
    loss.backward()
    # 打印 w,b 变量的梯度
    # backward 函数计算的梯度值会存储在张量的 grad 变量中 print("W 的梯度:", w.grad)
    print("b 的梯度", b.grad)

输出结果：

W 的梯度：tensor(
[[0.0757, 0.6087, -0.6538], [ 0.0757, 0.6087, -0.6538], [ 0.0757, 0.6087, - 0.6538], [ 0.0757, 0.6087,
-0.6538], [ 0.0757, 0.6087, -0.6538]])

b 的梯度 tensor([ 0.0757, 0.6087, - 0.6538])

总结

本小节主要讲解了 PyTorch 中非常重要的自动微分模块的使用和理解。
我们对需要计算梯度的张量需要设置 requires_grad=True 属性。

案例 - 线性回归案例

• 知道线性回归是什么

• 知道损失函数是什么

• 知道线性回归的梯度下降优化方法

线性回归

假若有了身高和体重数据，来了播仔的身高，你能预测播仔体重吗？

编号	身高	体重
1	160	56.3
2	166	60.6
3	172	65.1
4	174	68.5
5	180	75
6	176	?

思路：先从已知身高 X 和体重 Y 中找规律，再预测

方程 y = WX + b

W160 + b = 56.3 -- (1)
W166 + b = 60.6 – - (2)
...
W: 斜率 b:截距
若：y = 0.9 x + (-93)
  0.9*176 +(-93)= ?

损失函数

损失函数用来衡量真实值和预测值之间的差异，为优化参数指明了方向

均方误差 (Mean-Square Error, MSE)

平均绝对误差 (Mean Absolute Error , MAE)

梯度下降法 - 梯度下降和梯度

• 什么是梯度下降法

• 顾名思义：沿着梯度下降的方向求解极小值

• 举个例子：坡度最陡下山法

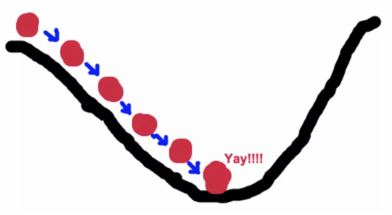
梯度下降过程就和下山场景类似

可微分的损失函数，代表着一座山寻找的函数的最小值，也就是山底

• 输入：初始化位置 S；每步距离为 a。输出：从位置 S 到达山底

• 步骤 1：令初始化位置为山的任意位置 S

• 步骤 2：在当前位置环顾四周，如果四周都比 S 高返回 S；否则执行步骤 3

• 步骤 3: 在当前位置环顾四周，寻找坡度最陡的方向，令其为 x 方向

• 步骤 4：沿着 x 方向往下走，长度为 a，到达新的位置 S‘

• 步骤 5：在 S‘位置环顾四周，如果四周都比 S‘高，则返回 S‘ 。否则转到步骤 3

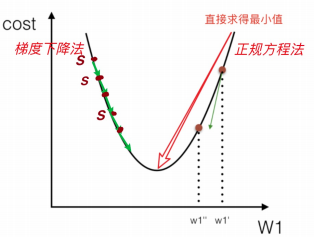
梯度下降法 - 梯度下降和梯度

什么是梯度 gradient grad
• 单变量函数中，梯度就是某一点切线斜率（某一点的导数）；有方向为函数增长最快的方向
• 多变量函数中，梯度就是某一个点的偏导数；有方向：偏导数分量的向量方向
梯度下降公式
• 循环迭代求当前点的梯度，更新当前的权重参数
• α: 学习率(步长) 不能太大, 也不能太小. 机器学习中：0.001 ~ 0.01
• 梯度是上升最快的方向，我们需要是下降最快的方向，所以需要加负号

梯度下降法 - 梯度下降和梯度

单变量梯度下降 – 举个栗子

函数：J(θ) = θ", 求当 θ 为何值时，J(θ) 值最小 J(θ) 函数关于 θ 的导数为：2θ

初始化：起点为：1，学习率：α = 0.4

我们开始进行梯度下降的迭代计算过程：第一步：θ = 1

第二步：θ = θ - α * (2θ) = 1 - 0.4 * (2*1) = 0.2

第三步：θ = θ - α * (2θ) = 0.2 - 0.4 * (2*0.2) = 0.04

第四步：θ = θ - α * (2θ) = 0.04 - 0.4 * (2*0.04) = 0.008

第五步：θ = θ - α * (2θ) = 0.008 - 0.4 * (2*0.008) = 0.0016

....

第 N 步：θ 已经极其接近最优值 0，J(θ) 也接近最小值。

小结：经过四次的运算，即走了四步，基本抵达了函数的最低点

梯度下降法 - 梯度下降和梯度

梯度下降优化过程
1. 给定初始位置、步长（学习率）
2. 计算该点当前的梯度的负方向
3. 向该负方向移动步长
4. 重复 2-3 步直至收敛
  • 两次差距小于指定的阈值
  • 达到指定的迭代次数
梯度下降公式中，为什么梯度要乘以一个负号
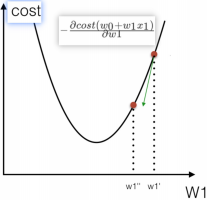
• 梯度的方向实际就是函数在此点上升最快的方向！
• 需要朝着下降最快的方向走，负梯度方向，所以加上负号
有关学习率步长 (Learning rate)
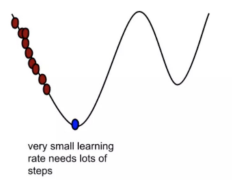
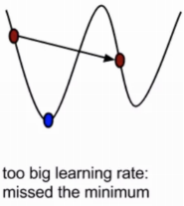
1. 步长决定了在梯度下降迭代的过程中，每一步沿梯度负方向前进的长度
2. 学习率太小，下降的速度会慢
3. 学习率太大：容易造成错过最低点、产生下降过程中的震荡、甚至梯度爆炸

模型构建

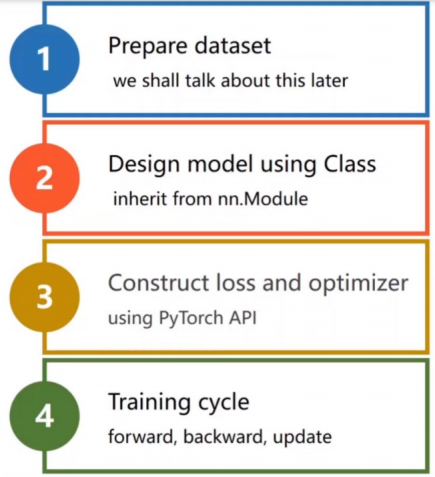
我们使用 PyTorch 的各个组件来构建线性回归的实现。在 pytorch 中进行模型构建的整个流程一般分为四个步骤：

准备训练集数据
构建要使用的模型
设置损失函数和优化器
模型训练

要使用的 API

使用 PyTorch 的 nn.MSELoss() 代替自定义的平方损失函数
使用 PyTorch 的 data.DataLoader 代替自定义的数据加载器
使用 PyTorch 的 optim.SGD 代替自定义的优化器
使用 PyTorch 的 nn.Linear 代替自定义的假设函数

1、导入工具包

python

# 导入相关模块
import torch
from torch.utils.data import TensorDataset  # 构造数据集对象
from torch.utils.data import DataLoader  # 数据加载器
from torch import nn  # nn 模块中有平方损失函数和假设函数 from torch import optim  # optim 模块中有优化器函数
from sklearn.datasets import make_regression  # 创建线性回归模型数据集
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签  plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

2、数据集构建

python

def create_dataset():
    x, y, coef = make_regression(n_samples=100, n_features=1,
                                 noise=10,
                                 coef=True,
                                 bias=1.5,
                                 random_state=0)

    # 将构建数据转换为张量类型
    x = torch.tensor(x)
    y = torch.tensor(y)
    return x, y, coef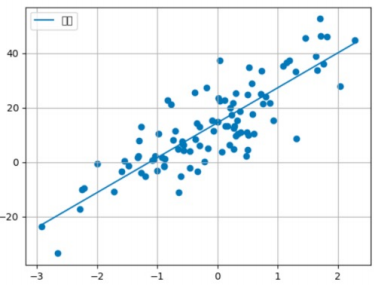

python

if __name__ == "__main__":
    # 生成的数据
    x, y, coef = create_dataset()
    # 绘制数据的真实的线性回归结果
    plt.scatter(x, y)
    x = torch.linspace(x.min(), x.max(), 1000)
    y1 = torch.tensor([v * coef + 1.5 for v in x])
    plt.plot(x, y1, label='real')
    plt.grid()
    plt.legend()
    plt.show()

使用 dataloader 构建数据加载器并进行模型构建

python

# 构造数据集
x, y, coef = create_dataset()
# 构造数据集对象
dataset = TensorDataset(x, y)
# 构造数据加载器
# dataset=:数据集对象
# batch_size=:批量训练样本数据  # shuffle=:样本数据是否进行乱序
dataloader = DataLoader(dataset=dataset, batch_size=16, shuffle=True)
# 构造模型
# in_features 指的是输入张量的大小 size  # out_features 指的是输出张量的大小 size
model = nn.Linear(in_features=1, out_features=1)

3、设置损失函数和优化器

python

# 构造平方损失函数
criterion = nn.MSELoss()
# 构造优化函数
optimizer = optim.SGD(params=model.parameters(), lr=1e-2)

4、模型训练

python

epochs = 100
# 损失的变化
loss_epoch = []
total_loss = 0.0
train_sample = 0.0
for _ in range(epochs):
    for train_x, train_y in dataloader:
        # 将一个 batch 的训练数据送入模型
        y_pred = model(train_x.type(torch.float32))
        # 计算损失值
        loss = criterion(y_pred, train_y.reshape(-1, 1).type(torch.float32))
        total_loss += loss.item()
        train_sample += len(train_y)
        # 梯度清零
        optimizer.zero_grad()
        # 自动微分 (反向传播)
        loss.backward()
        # 更新参数
        optimizer.step()
    # 获取每个 batch 的损失
    loss_epoch.append(total_loss / train_sample)

5、构建训练模型函数

python

# 绘制损失变化曲线
plt.plot(range(epochs), epoch_loss)
plt.title('损失变化曲线')
plt.grid()
plt.show()
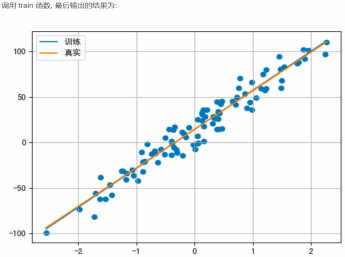
# 绘制拟合直线
plt.scatter(x, y)
x = torch.linspace(x.min(), x.max(), 1000)
y1 = torch.tensor([v * model.weight + model.bias for v in x])
y2 = torch.tensor([v * coef + 1.5 for v in x])
plt.plot(x, y1, label='训练')
plt.plot(x, y2, label='真实')
plt.grid()
plt.legend()
plt.show()

PyTorch 使用 ​

张量的基本类型 ​

张量的创建 ​

基本创建方式 ​

创建线性和随机张量 ​

创建 0-1 张量 ​

张量的类型转换 ​

张量的类型转换 ​

张量转换为 NumPy 数组 ​

NumPy 数组转换为张量 ​

标量张量和数字转换 ​

张量数值计算 ​

张量基本运算 ​

点乘运算 ​

张量运算函数 ​

张量索引操作 ​

简单行、列索引 ​

列表索引 ​

范围索引 ​

布尔索引 ​

多维索引 ​

张量形状操作 ​

reshape() 函数 ​

squeeze() 和 unsqueeze() 函数 ​

transpose() 和 permute() 函数 ​

view() 和 contiguous() 函数 ​

张量拼接操作 ​

自动微分模块 ​

案例 - 线性回归案例 ​

线性回归 ​

损失函数 ​

模型构建 ​

PyTorch 使用

张量的基本类型

张量的创建

基本创建方式

创建线性和随机张量

创建 0-1 张量

张量的类型转换

张量的类型转换

张量转换为 NumPy 数组

NumPy 数组转换为张量

标量张量和数字转换

张量数值计算

张量基本运算

点乘运算

张量运算函数

张量索引操作

简单行、列索引

列表索引

范围索引

布尔索引

多维索引

张量形状操作

reshape() 函数

squeeze() 和 unsqueeze() 函数

transpose() 和 permute() 函数

view() 和 contiguous() 函数

张量拼接操作

自动微分模块

案例 - 线性回归案例

线性回归

损失函数

模型构建