支持向量机

支持向量机（Support Vector Machine，SVM），以下简称 SVM) 虽然诞生只有短短的二十多年，但是自一诞生便由于它良好的分类性能席卷了机器学习领域，并牢牢压制了神经网络领域好多年。如果不考虑集成学习的算法，不考虑特定的训练数据集，在分类算法中的表现 SVM 说是排第一估计是没有什么异议的。

SVM 是一个二元分类算法，线性分类和非线性分类都支持。经过演进，现在也可以支持多元分类，同时经过扩展，也能应用于回归问题。

SVM 的最大特点是能构造出[最大间距]的决策边界，从而提高分类算法的鲁棒性（健壮和强壮的意思）。

最大间隔分类器

最大间隔分类器（Maximum Margin Classifier），硬间隔分类器

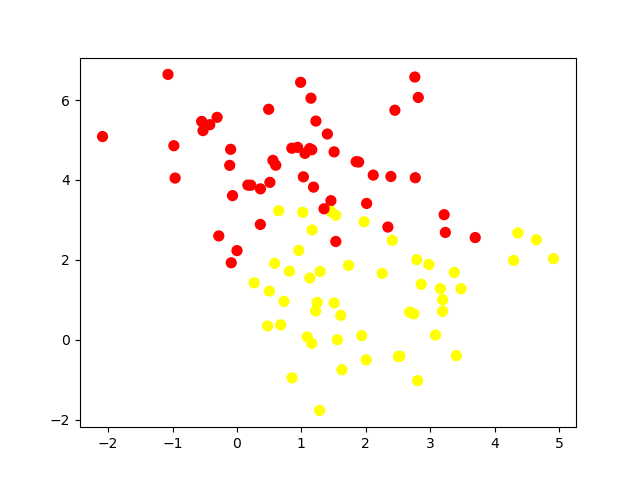
假设桌子上我放了红色和黄色两种球，请你用一根棍子将这两种颜色的球分开。

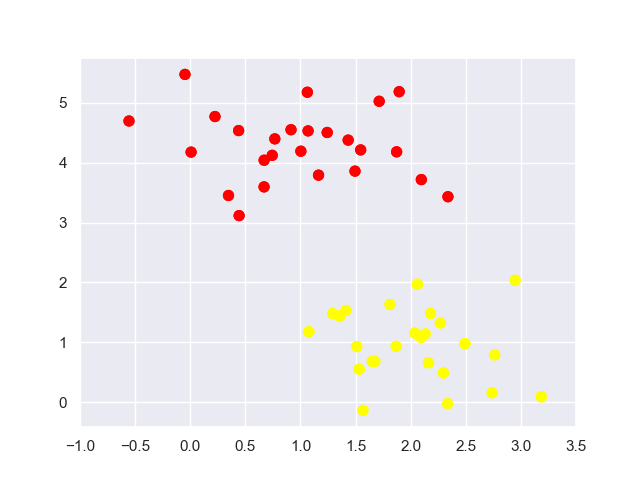
你可以很快想到解决方案，在红色和黄色球之间画条直线就好了，如下图所示：

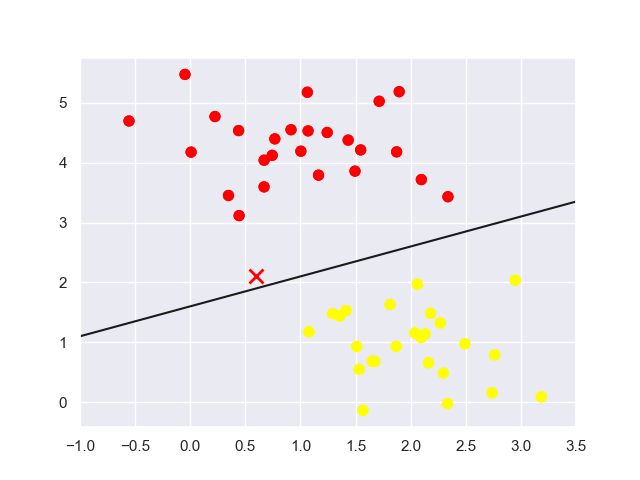
其中的那条线就是 SVC 决策边界（decision boundary）

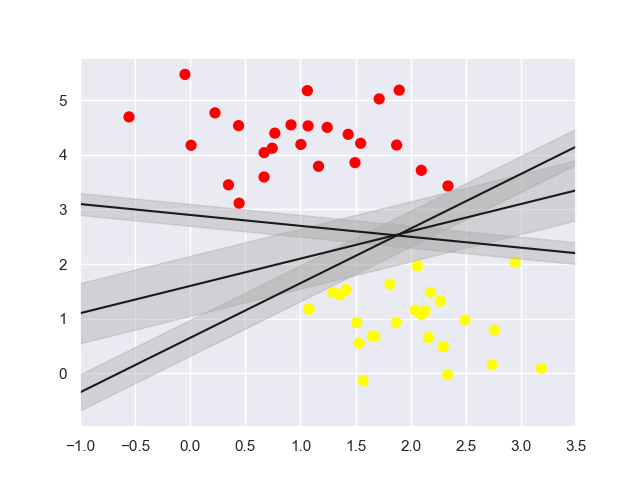
假如数据是完全的线性可分的，那么学习到的模型可以称为硬间隔支持向量机。换个说法，硬间隔指的就是完全分类准确，不能存在分类错误的情况。软间隔，就是允许一定量的样本分类错误。

我们知道，实际工作中的数据没有那么“干净”，或多或少都会存在一些噪点。所以线性可分是个理想情况。这时，我们需要使用到软间隔 SVM（近似线性可分）

数学原理

假设要对一个数据集进行分类，可以构造一个分隔线把圆形的点和方形的点分开。这个分隔线称为[分隔超平面]（Separating hyperplane）。

从下图图中可以明显看出，实线的分隔线比虚线的分隔线更好，因为使用实线的分隔线进行分类时，离分隔线最近的点到分隔线上的距离更大，即 margin2>margin1。这段距离的两倍，称为[间距]（margin）。那些离分隔超平面最近的点，称为[支持向量]（support vector）。为了达到最好的分类效果，SVM 的算法原理就是要找到一个分隔超平面，它能[把数据集正确地分类]，并且[间距最大]。

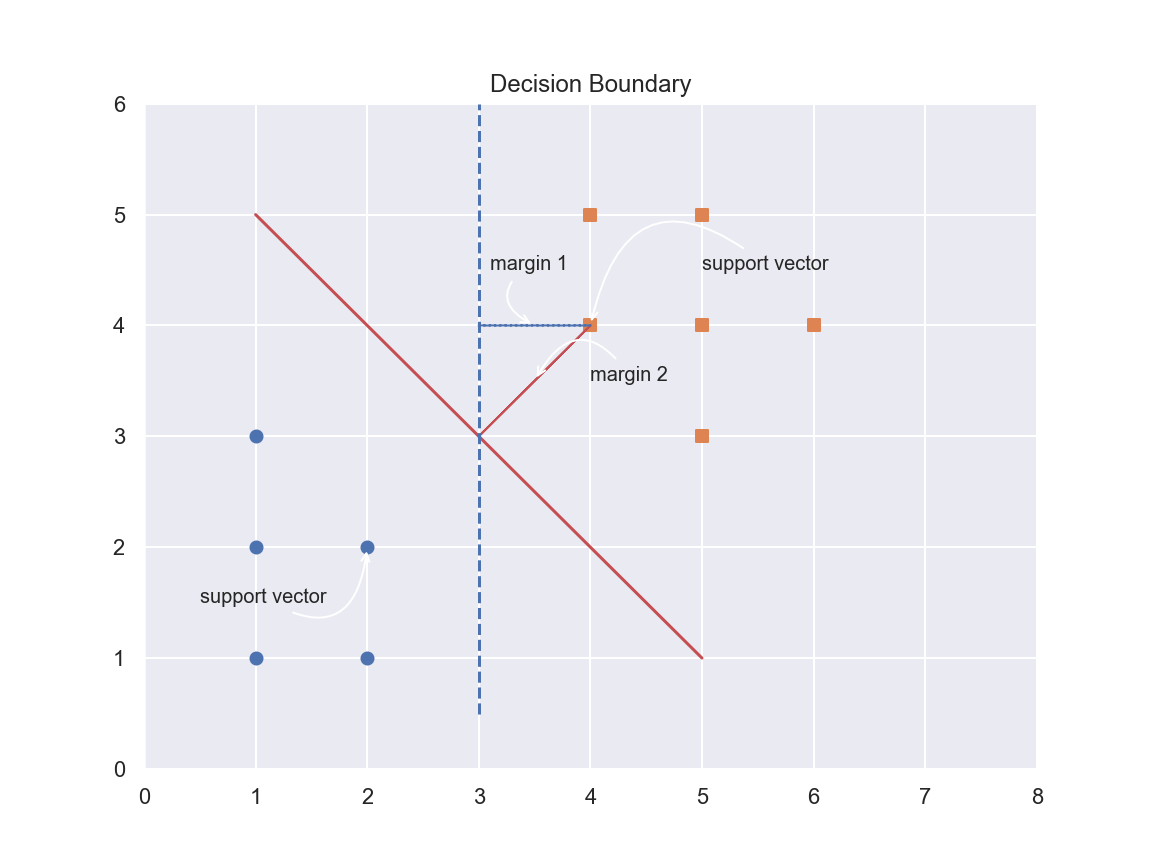
在二维空间里，可以使用方程 w~1~x~1~+w~2~x~2~+b=0 来表示分隔超平面。针对高维度空间，可写成一般化的向量形式，即 w^T^x+b=0。我们画出与分隔超平面平行的两条直线，分别穿过两个类别的支持向量（离分隔超平面距离最近的点）。这两条直线的方程分别为 w^T^x+b=-1 和 w^T^x+b=1。

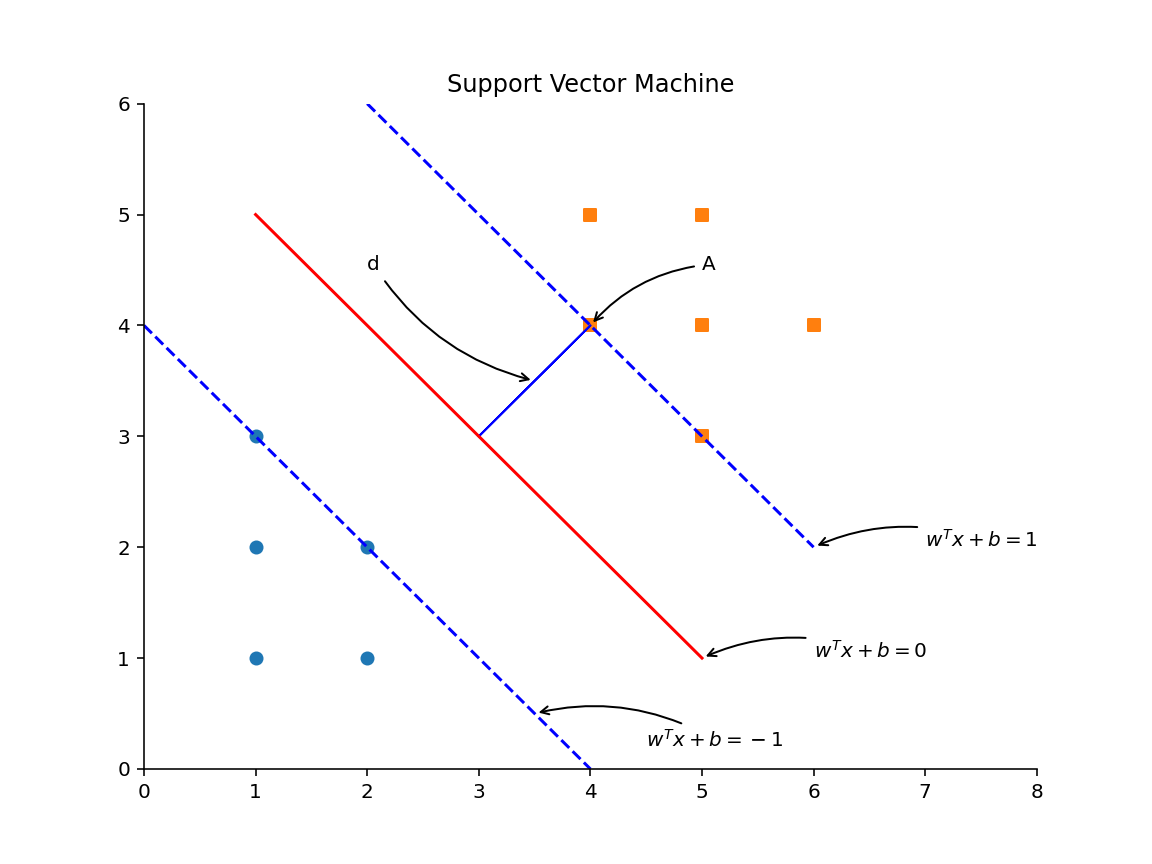
根据点到直线的距离公式，可以容易地算出支持向量 A 到分隔超平面的距离为：

$$d=\frac{|(w^{T}A+b)|}{||w||}$$

由于点 A 在直线 w^T^x+b=1 上，因此 w^T^A+b=1，代入即可得，支持向量 A 到分隔超平面的距离为 $\gamma =\frac{1}{||w||}$ , 为了使间距最大，我们只需要找到合适的参数 w 和 b，使 $\frac{1}{||w||}$ 最大即可。$||w||$ 是向量 w 的 L2 范数，其计算公式为：

$$\begin{gathered} ||w||=\sqrt{ \\ \sum _{i=1}^n{w}_i^2} \end{gathered}$$

由此可得，求 $\frac{1}{||w||}$ 的最大值，等价于求 $ǁw{ǁ}^2$ 最小值：

$$||w||=\sqrt{\sum _{j=1}^n{w}_j^2}$$

其中 n 为向量 w 的维度。除了间距最大外，我们选出来的分隔超平面还要能正确地把数据集分类。问题来了，怎样在数学上表达出“正确地把数据集分类”这个描述呢？

可以容易地得出结论，针对方形的点，必定满足 w^T^x+b≥1 的约束条件。针对圆形的点 x，必定满足 w^T^x+b≤-1 的约束条件。类别是离散的值，我们使用 -1 来表示圆形的类别，用 1 来表示方形的类别，即 y∈{-1,1}。针对数据集中的所有样本 x^（i）^，y^（i）^，只要它们都满足以下的约束条件，则由参数 w 和 b 定义的分隔超平面即可正确地把数据集分类：

$$y^{(i)}(w^T{x}^i+b)\ge 1$$

其技巧在于使用 1 和 -1 来定义类别标签。针对 y^（i）^=1 的情况，由于其满足 w^T^x^（i）^+b≥1 的约束，两边都乘以 y^（i）^后，大于号保持不变。针对 y^（i）^=-1 的情况，由于其满足 w^T^x^（i）^+b≤-1 的约束，两边都乘以 y^（i）^后，负负得正，并且小于号变成了大于号。这样，我们就可以用一个公式来表达针对两个不同类别的约束函数了。

在逻辑回归算法里，使用 0 和 1 作为类别标签，而在这里我们使用 -1 和 1 作为类别标签。其目的都是为了让数学表达尽量简洁。

一句话总结：求解 SVM 算法，就是在满足约束条件 y^（i）^（w^T^x^（i）^+b）≥1 的前提下，求解$\Vert w{\Vert }^2$的最小值。

软间隔分类器

Support Vector Classifier (SVC, 软间隔分类器)

数学原理

针对线性不可分的数据集，最大间隔分类器就失灵了。因为无法找到最大间距的分隔超平面，解决这个问题的办法是引入一个参数ε，称为松弛系数。然后把优化的目标函数变为：

$$\begin{gathered} ||w|{|}^2+R\sum _{ \\ i=1}^m{\epsilon }_i \end{gathered}$$

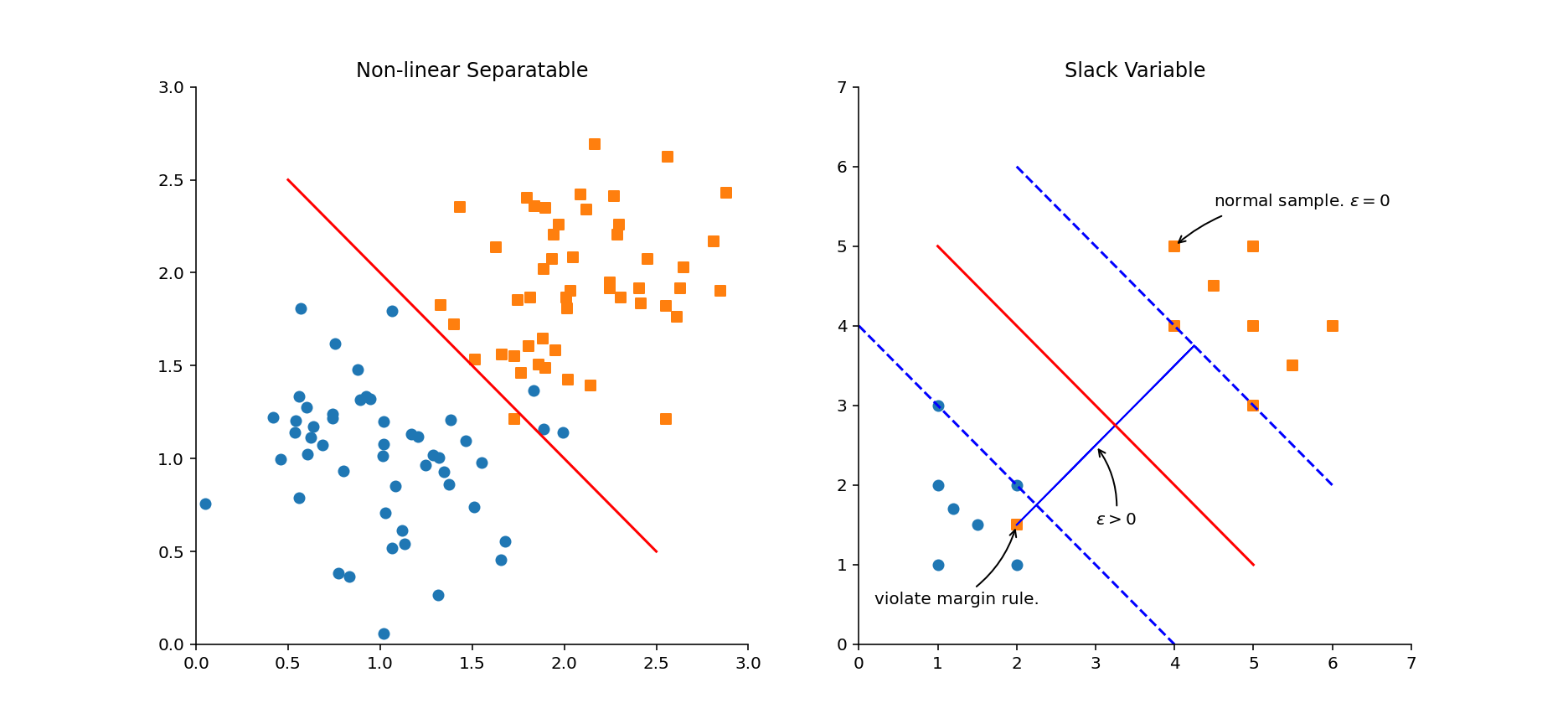
其中，m 为数据集的个数，R 为算法参数。其约束条件相应地变为：

$$y^{(i)}(w^T{x}^i+b)\ge 1-{\epsilon }_i$$

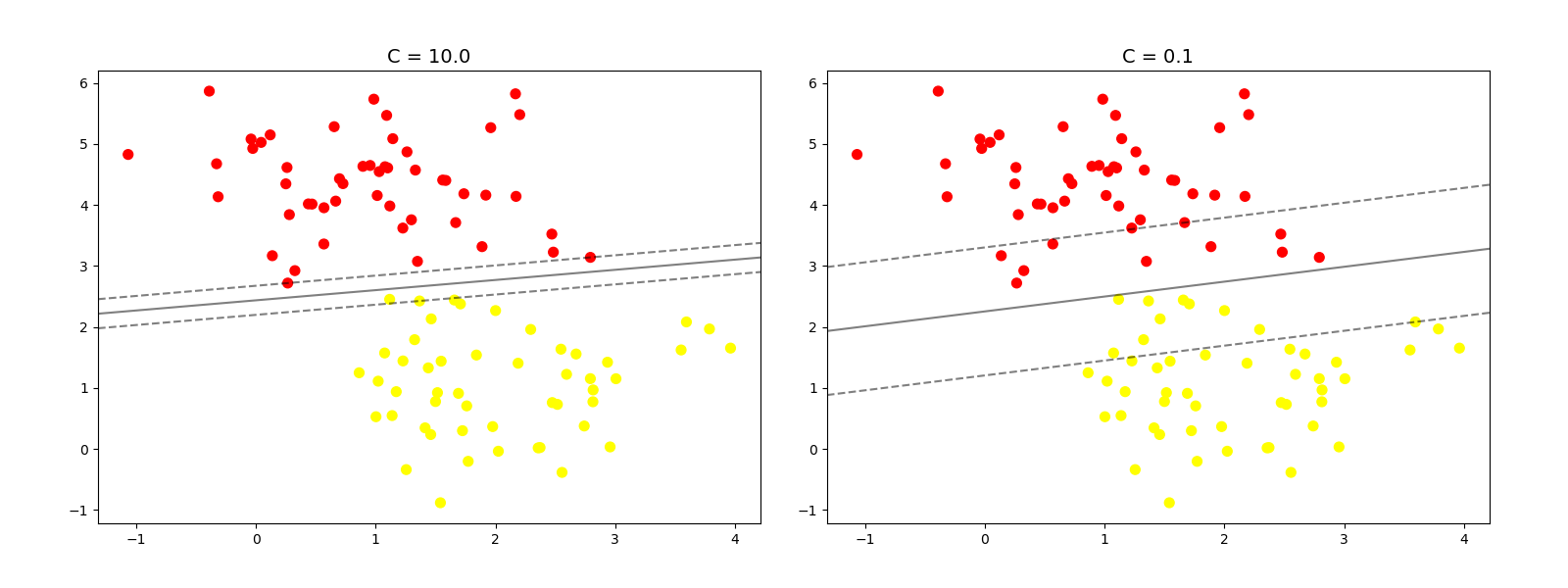
怎么理解松弛系数呢？我们可以把ε~i~理解为数据样本 x^（i）^违反最大间距规则的程度，针对大部分“正常”的样本，即满足约束条件的样本ε=0。而对部分违反最大间距规则的样本ε＞0。而参数 R 则表示对违反最大间距规则的样本的“惩罚”力度。当 R 选择一个很大的值时，我们的目标函数对违反最大间距规则的点的“惩罚力度”将变得很大。当 R 选择一个比较小的值时，针对那些违反最大间距规则的样本，其“付出的代价”不是特别大，我们的模型就会倾向于允许部分点违反最大间距规则。我们可以把 y^（i）^（w^T^x^（i）^+b）作为横坐标，把样本由于违反约束条件所付出的代价 J~i~作为纵坐标，

从图 8-4 可以清楚地看出来，针对那些没有违反约束条件 y^（i）^（w^T^x^（i）^+b）≥1 的样本，其成本为 0。而针对那些违反了约束条件的样本 y^（i）^（w^T^x^（i）^+b）≥1-ε~i~ ，其成本与ε成正比，斜线的斜率为 R。

从这里的描述可知，引入松弛系数类似于逻辑回归算法里的成本函数引入正则项，目的都是为了纠正过拟合问题，让支持向量机对噪声数据有更强的适应性。当出现一些违反大间距规则的噪声样本时，仍然希望我们的分隔超平面是原来的样子，这就是松弛系数的作用。

支持向量机（SVM）

SVM = SVC + 非线性核函数

比如下面的样本集就是个非线性的数据。图中的两类数据，分别分布为两个圆圈的形状。那么这种情况下，不论是多高级的分类器，只要映射函数是线性的，就没法处理，SVM 也处理不了。这时，我们需要引入一个新的概念：核函数。它可以将样本从原始空间映射到一个更高维的特质空间中，使得样本在新的空间中线性可分。这样我们就可以使用原来的推导来进行计算，只是所有的推导是在新的空间，而不是在原来的空间中进行。

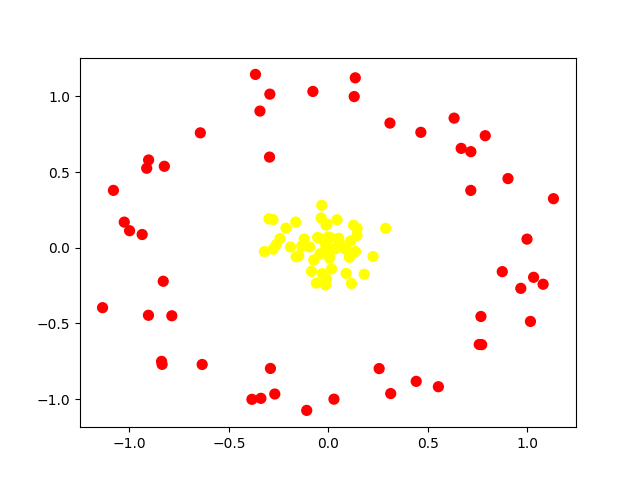
所以在非线性 SVM 中，核函数的选择就是影响 SVM 最大的变量。最常用的核函数有线性核、多项式核、高斯核、拉普拉斯核、sigmoid 核，或者是这些核函数的组合。这些函数的区别在于映射方式的不同。通过这些核函数，我们就可以把样本空间投射到新的高维空间中。

当然软间隔和核函数的提出，都是为了方便我们对上面超平面公式中的 w 和 b 进行求解，从而得到最大分类间隔的超平面。

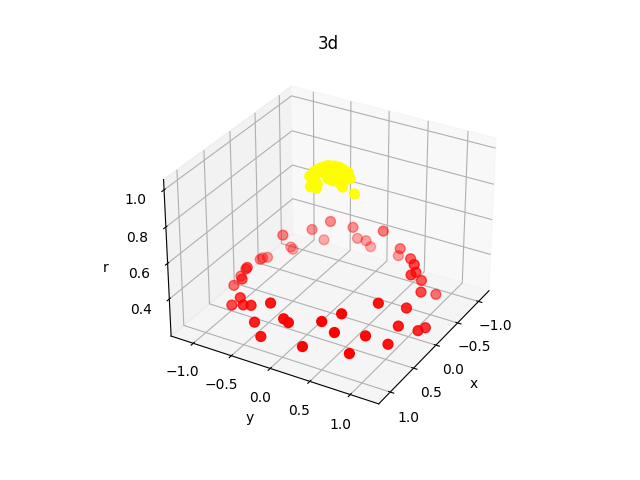
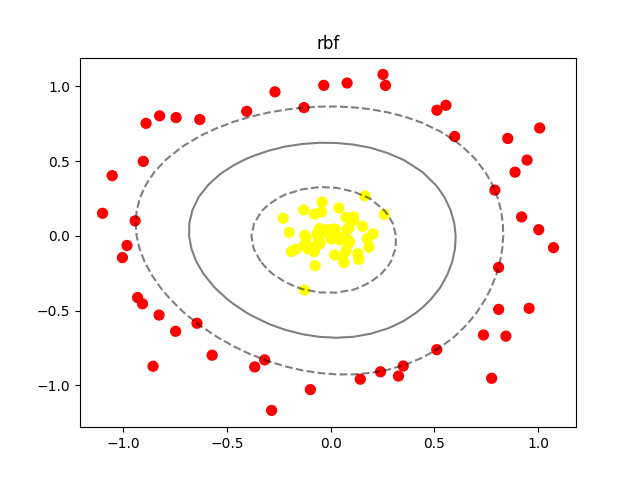
核函数有很多种

• linear kernel（线性核函数）
• Polynomial kernel（多项式核函数）
• RBF kernel（高斯核函数（默认））
• Sigmoid kernel（sigmoid 核函数）

最简单的核函数

支持向量机需要找出合适的参数 w，b，使得由它们决定的分隔超平面、间距最大，且能正确地对数据集进行分类。间距最大是我们的优化目标，正确地对数据集进行分类是约束条件。用数学来表达，在满足约束条件 $ y^{(i)}w^{(T)}x^{(i)}+b≥1$ ，即 $ y^{(i)}w^{(T)}x^{(i)}+b≥1$ 的前提下，求 $\frac{1}{2}||w|{|}^2$ 的最小值。

拉格朗日乘子法是解决约束条件下，求函数极值的理想方法。其方法是引入非负系数α来作为约束条件的权重：

$$L=\frac{1}{2}||w|{|}^2-\sum _{i=1}^m{\alpha }_i(y^{(i)}(w^{(T)}{x}^{(i)}+b)-1)$$

公式中，针对数据集中的每个样本 $x^{(i)}$，$y^{(i)}$，都有一个系数 ${\alpha }_i$ 与之对应。学习过微积分的读者都知道，极值处的偏导数为 0。我们先求 $L$ 对 $w$ 的偏导数：

$$\frac{\partial L}{\partial w}=w-\sum _{i=1}^m{\alpha }_i{y}^i{x}^i=0$$

从而得到 $w$ 和 $\alpha$ 的关系：

$$w=\sum _{i=1}^m{\alpha }_i{y}^i{x}^i$$

将 $\frac{2}{||w||}$ 的最大值转化为 $\frac{1}{2}||w|{|}^2$ 的最小值。其目的是为了使得 $w$ 的数学表达尽量简洁优美。接着我们继续先求 $L$ 对 $b$ 的偏导数：

$$\frac{\partial L}{\partial b}=\sum _{i=1}^m{\alpha }_i{y}^i=0$$

把 $w=\sum _{i=1}^m{\alpha }_i{y}^i{x}^i$ 和 $\sum _{i=1}^m{\alpha }_i{y}^i=0$ 带入 $L$ 通过代数运算可得：

$$L=\sum _{i=1}^m{\alpha }_i-\frac{1}{2}{\alpha }_i{\alpha }_j{y}^{(i)}{y}^{(j)}{x}^{(i)T}{x}^{(j)}$$

这个公式看起来很复杂。我们解释一下公式里各个变量的含义。其中，$m$ 是数据集的个数，$\alpha$ 是拉格朗日乘子法引入的一个系数，针对数据集中的每个样本 $x^{(i)}$，都有对应的 ${\alpha }_i$ ，$x^{(i)}$

是数据集中第 $i$ 个样本的输入，它是一个向量，$y^{(i)}$

是数据集第 $i$ 个样本的输出标签，其值为 $y^{(i)}\in \{1,1\}$ 。

怎么求这个公式的最小值，是数值分析 (numerical analysis）这个数学分支要解决的问题，这是一个典型的二次规划问题。目前广泛应用的是一个称为 SMO（序列最小优化）的算法。这些内容不再进一步展开，感兴趣的读者可以查阅相关资料。

最后求解出来的 $\alpha$ 有个明显的特点，即大部分 ${\alpha }_i=0$，这个结论背后的原因很直观，因为只有那些支持向量所对应的样本，直接决定了间隙的大小，其他离分隔超平面太远的样本，对间隙大小根本没有影响。

用拉格朗日乘子法加上一大堆偏导数运算，最后推导出来的公式复杂到无法展开进一步论述其求解方法，那么做这些事情和公式推导的意义在哪里呢？实际上，推导出这个公式的主要目的是为了引入支持向量机的另外一个核心概念：核函数。

我们注意到 L 里的 $x^{(i)T}{x}^{(j)}$ 部分，其中 $x^{(i)}$ 是一个特征向量，所以 $x^{(i)T}{x}^{(j)}$ 是一个数值，它是两个输入特征向量的内积。另外，我们的预测函数为：

$$\hat{y}=\sum _{i=1}^m{\alpha }_i-\frac{1}{2}{\alpha }_i{\alpha }_j{y}^{(i)}{y}^{(j)}{x}^{(i)T}{x}^{(j)}x$$

当 $\hat{y}>0$ 时我们预测为类别 1，当 $\hat{y}<0$ 时，我们预测为类别 -1。注意到预测函数里也包含式子 $x^{(i)T}x$ ， $K(x^{(i)}，x^{(j)})=x^{(i)T}{x}^{(j)}$ 就是核函数。$x^{(i)T}{x}^{(j)}$ 是两个向量内积，它的物理含义是衡量两个向量的相似性，典型地，当这两个向量相互垂直时，即完全线性无关，此时$x^{(i)T}{x}^{(j)}=0$ 。引入核函数后，我们的预测函数就变成：

$$\hat{y}=\sum _{i=1}^m{\alpha }_i{y}^{(i)}K(x^{(i)},x)+b$$

把方形类别的约束定义为 $w^{T}x+b\ge 1$，把圆形类别的约束定义为 $w^{T}x+b\le -1$。而这里的预测函数，又以 0 为分界点，即针对输入特征向量 $x$，当 $w^{T}x+b＞0$ 时，预测为方形类别。

常用核函数

核函数一般和应用场景相关，例如我们说的在基因测序领域和在文本处理领域，它们的核函数可能是不一样的，有专门针对特定应用领域进行核函数开发和建模的科研人员在从事这方面的研究。虽然核函数和应用场景相关，但实际上还是有一些通用的、“万金油”式的核函数。常用的核函数有两种，一种是多项式核函数，顾名思义，是对输入特征向量增加多项式的一种相似性映射函，其数学表达为：

$$K(x^{(i)},x^{(j)})=(\gamma x^{(i)T}+c{)}^n$$

其中 $\gamma$ 为正数，$c$ 为非负数。我们介绍过的线性核函数 $K(x^{(i)}，x^{(j)})=x^{(i)T}{x}^{(j)}$ 是多项式核函数在 $n=1,\gamma =1,c=0$ 处的一个特例。在二维空间里 $K(x^{(i)}，x^{(j)})=x^{(i)T}{x}^{(j)}$ 只能表达直线的分隔超平面

而多项式核函数 $K(x^{(i)},x^{(j)})=(\gamma x^{(i)T}+c{)}^n$ 在 n＞1 时，可以表达更复杂的、非直线的分隔超平面。另外一个常用的核函数是高斯核函数，其数学表达式为：

$$\begin{gathered} K(x^{(i)},x^{(j)})=exp \\ ⟮ \\ -\frac{(x(i)-x^{(j)}{)}^2}{2{\sigma }^2}⟯ \end{gathered}$$

如果我们的输入特征是一维的标量，那么高斯核函数对应的形状就是一个反钟形的曲线，其参数σ控制反钟形的宽度

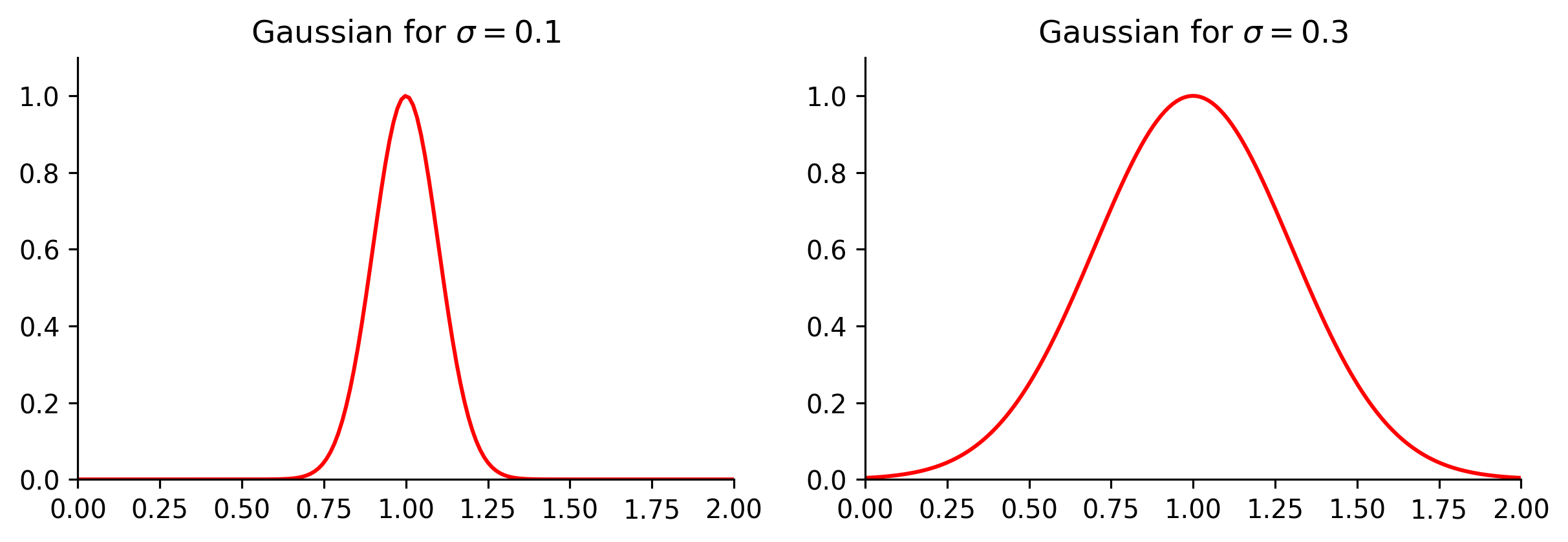
接下来对比一下几个核函数进行对比，看看它们各有哪些优缺点

线性函数

$$K(x^{(i)}，x^{(j)})=x^{(i)T}{x}^{(j)}$$

这是我们接触到的最简单的核函数，它直接计算两个输入特征向量的内积。它的优点是简单、运算效率高，因为不涉及复杂的变换；结果容易解释，因为总是能生成一个最简洁的线性分隔超平面。它的缺点也很明显，即对线性不可分的数据集没有很好的办法。

多项式核函数

$$K(x^{(i)},x^{(j)})=(\gamma x^{(i)T}+c{)}^n$$

多项式核函数通过多项式来作为特征映射函数，它的优点是可以拟合出复杂的分隔超平面。它的缺点是可选的参数太多，有γ，c，n 这 3 个参数要选择，在实践过程中，选择一组合适的参数会变得比较困难；另外一个缺点是，多项式的阶数 n 不宜太高，否则会给模型求解带来一些计算的困难。典型地，当 $x^{(i)T}{x}^{(j)}<1$ 时，经过 n 次方运算后，会接近于 0，而当 $x^{(i)T}{x}^{(j)}>1$ 时，经过 n 次方运算后，又会变得非常大，这样核函数就会变得不够稳定。

高斯核函数

$$\begin{gathered} K(x^{(i)},x^{(j)})=exp \\ ⟮ \\ -\frac{(x(i)-x^{(j)}{)}^2}{2{\sigma }^2}⟯ \end{gathered}$$

高斯核函数可以把输入特征映射到无限多维，所以它会比线性核函数功能上要强大很多，并且没有多项式核函数的数值计算那么困难，因为它的核函数计算出来的值永远在[0，1]之间。高斯核函数还有一个优点是参数容易选择，因为它只有一个参数σ。它的缺点是不容易解释，因为映射到无限多维向量空间这个事情显得太不直观；计算速度比较慢；容易造成过拟合，原因是映射到无限维向量空间，这是个非常复杂的模型，它会试图去拟合所有的样本，从而造成过拟合。

总结

SVM 分类器，它在文本分类尤其是针对二分类任务性能卓越。同样，针对多分类的情况，我们可以采用一对多，或者一对一的方法，多个二值分类器组合成一个多分类器。

另外关于 SVM 分类器的概念，我希望你能掌握以下的三个程度：

1. 完全线性可分情况下的线性分类器，也就是线性可分的情况，是最原始的 SVM，它最核心的思想就是最找到大的分类间隔；
2. 大部分线性可分情况下的线性分类器，引入了软间隔的概念。软间隔，就是允许一定量的样本分类错误；
3. 线性不可分情况下的非线性分类器，引入了核函数。它让原有的样本空间通过核函数投射到了一个高维的空间中，从而变得线性可分。

在 SVM 的推导过程中，有大量的数学公式，这里没有进行详细的推导演绎，因为除了写论文，大部分时候不会用到这些公式推导。

支持向量机是一种强大的分类方法，主要有四点理由。

• 模型依赖的支持向量比较少，说明它们都是非常精致的模型，消耗内存少。
• 一旦模型训练完成，预测阶段的速度非常快。
• 由于模型只受边界线附近的点的影响，因此它们对于高维数据的学习效果非常好——即使训练比样本维度还高的数据也没有问题，而这是其他算法难以企及的。
• 与核函数方法的配合极具通用性，能够适用不同类型的数据。

但是，SVM 模型也有一些缺点。

• 随着样本量 N 的不断增加，最差的训练时间复杂度会达到 [N3]；经过高效处理后，也只能达到 [N2]。因此，大样本学习的计算成本会非常高。
• 训练效果非常依赖于边界软化参数 C 的选择是否合理。这需要通过交叉检验自行搜索；当数据集较大时，计算量也非常大。
• 预测结果不能直接进行概率解释。这一点可以通过内部交叉检验进行评估（具体请参见 SVC 的 probability 参数的定义），但是评估过程的计算量也很大。

由于这些限制条件的存在，我通常只会在其他简单、快速、调优难度小的方法不能满足需求时，才会选择支持向量机。但是，如果你的计算资源足以支撑 SVM 对数据集的训练和交叉检验，那么用它一定能获得极好的效果。