线性回归

线性回归算法是使用 线性方程 对数据集进行拟合的算法，是一个非常常见的回归算法。本章首先从最简单的单变量线性回归算法开始介绍，然后介绍了多变量线性回归算法，其中成本函数以及梯度下降算法的推导过程会用到部分线性代数和偏导数；接着重点介绍了梯度下降算法的求解步骤以及性能优化方面的内容；最后通过一个房价预测模型，介绍了线性回归算法性能优化的一些常用步骤和方法。

应用场景

• 房价预测
• 销售额度预测
• 贷款额度预测

举例：

定义与公式

线性回归 (Linear regression) 是利用回归方程 (函数)对一个或多个自变量 (特征值) 和因变量 (目标值) 之间 关系进行建模的一种分析方式。

特点：只有一个自变量的情况称为单变量回归，多于一个自变量情况的叫做多元回归

通用公式：

$$98\begin{array}{rl}h(w)& =w_1{x}_1+w_2{x}_2+w_3{x}_3\cdots +b\\ & =w^T+b\end{array}$$

其中 w,x 可以理解为矩阵：

$$w=\left(\begin{array}{c}b\\ w_1\\ w_2\end{array}\right),x=\left(\begin{array}{c}1\\ x_1\\ x_2\end{array}\right)$$

线性回归用矩阵表示举例

$$\{\begin{array}{lr}1\times x_1+x_2=2& \\ 0\times x_1+x_2=2\\ 2\times x_1+x_2=3& \end{array}$$

写成矩阵形式

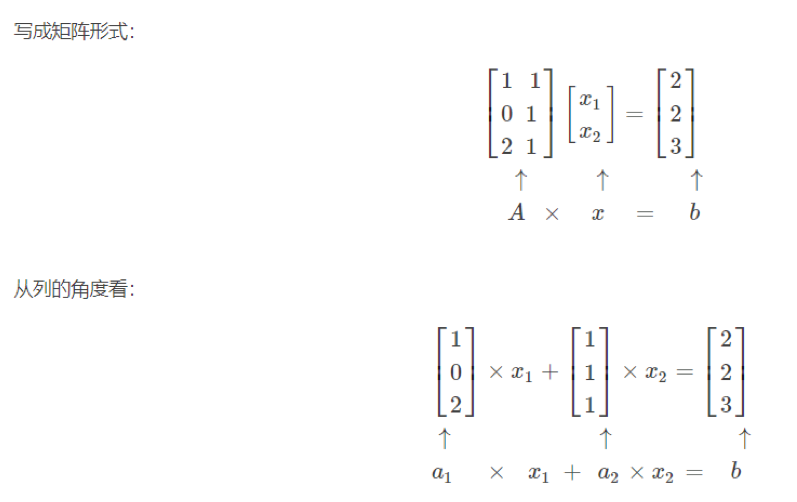
那么怎么理解呢？我们来看几个例子

• 期末成绩：0.7×考试成绩 +0.3×平时成绩
• 房子价格 = 0.02×中心区域的距离 + 0.04×城市一氧化氮浓度 + (-0.12×自住房平均房价) + 0.254×城镇犯罪率

上面两个例子，我们看到特征值与目标值之间建立了一个关系，这个关系可以理解为线性模型。

线性回归的特征

线性回归当中主要有两种模型，**一种是线性关系，另一种是非线性关系。**在这里我们只能画一个平面更好去理解，所以都用单个特征或两个特征举例子。

线性关系

单变量线性关系：

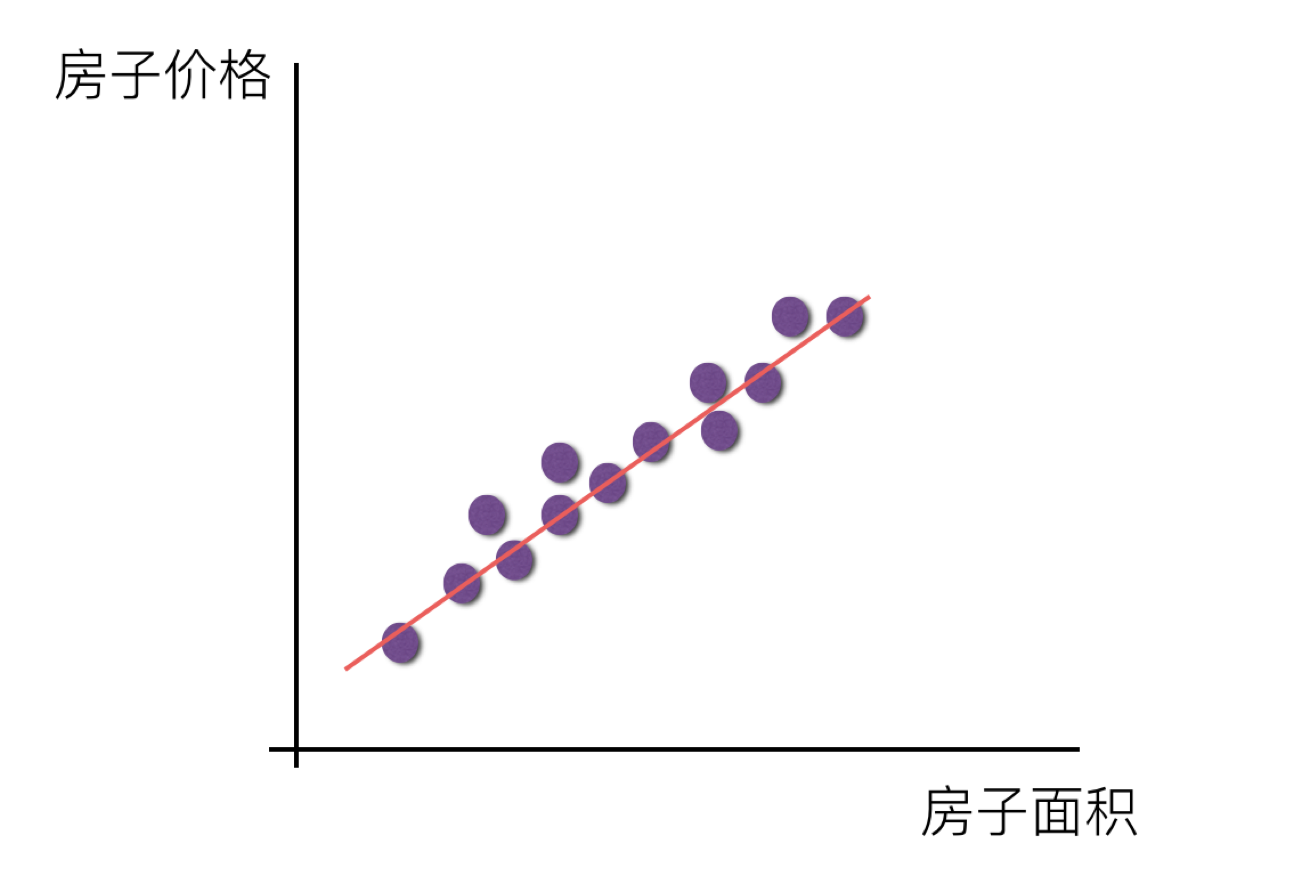
注释：单特征与目标值的关系呈直线关系，或者两个特征与目标值呈现平面的关系

更高维度的我们不用自己去想，记住这种关系即可

注意：利用回归方程 (函数)对一个或多个自变量 (特征值) 和因变量 (目标值) 之间关系进行建模的一种分析方式

线性方程

一元线性方程推导

让我们用一个简单的例子来引出线性回归模型。为了更形象地描述，假设我们有一个准备开咖啡店的的朋友小潘，他找朋友获取了一张人流量与日销售收入之间的关系表。

商场 ID	日均人流量（千人）	日均销售收入（千元）
1	2	12
2	5	31
3	8	45
4	8	52
5	13	79
6	15	85
7	17	115
8	19	119
9	21	135
10	24	145

小潘仔细研究了一下数据，似乎流量和收入是线性关系。这也很符合小潘的预期，为了更加直观地了解数据，验证他的猜测，他决定将数据可视化。他把上面的数据点表示在一个直角坐标系里。

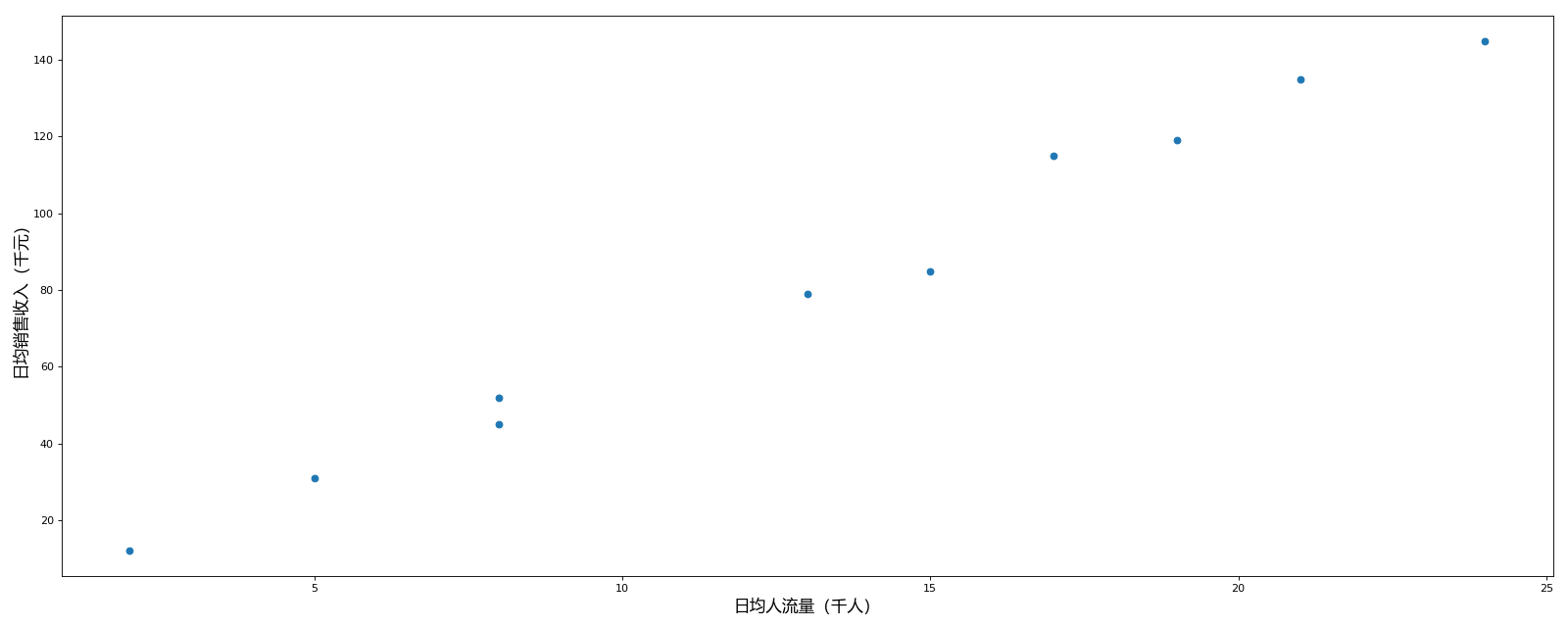
之后为了得出日均人流量与日均销售收入之间的关系，就可以现将现在的值与预测值绘写到表里面方便查看。

假设 h(x)=y=kx+b，那么 h(x~1~)=kx~1~+b

商场 ID	日均人流量（千人）	日均销售收入（千元）	实际值	预测值
1	2	12	h(x~1~)	y~1~
2	5	31	h(x~2~)	y~2~
3	8	45	h(x~3~)	y~3~
4	8	52	h(x~3~)	y~4~
5	13	79	h(x~3~)	y~5~
6	15	85	h(x~3~)	y~6~
7	17	115	h(x~3~)	y~7~
8	19	119	h(x~3~)	y~8~
9	21	135	h(x~3~)	y~9~
10	24	145	....

然后带入线性回归，为了是预测的线与实际的数据更加接近，就有

$$\begin{array}{rl}J(w)& =(h(x_1)-y_1{)}^2+(h(x_2)-y_2{)}^2+\cdots +(h(x_m)-y_m{)}^2\\ & =\sum _{i=1}^m(h(x_i)-y_i{)}^2\end{array}$$

上述函数也叫做 损失函数

如何去减少这个损失，使我们预测的更加准确些？既然存在了这个损失，我们一直说机器学习有自动学习的功能，在线性回归这里更是能够体现。这里可以通过一些优化方法去优化（其实是数学当中的求导功能）回归的总损失！！！

那么误差可以表示为

$$\begin{array}{rl}loss& =\sum _{i=1}^m(h(x_i)-y_i{)}^2\\ & =\sum _{i=1}^m((k{x}_i+b)-y_i{)}^2\end{array}$$

一般会把 Loss 求和平均，当做最终的损失，即总的误差为：

$$loss=\frac{1}{m}\sum _{i=1}^m(h(x_i)-y_i{)}^2$$

最小二乘法，就是选择 a 和 b 使 Loss 最小，可以求导计算极值，令每个变量的偏导数为 0，求方程组的解：

简化计算求得：

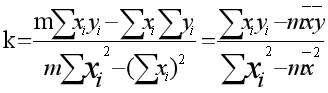
线性回归 API

sklearn.linear_model.LinearRegression()

• LinearRegression.coef_：回归系数

一元回归案例

from sklearn.linear_model import LinearRegression
import pandas as pd

# 1. 获取数据集
data = [
    [1, 2, 12],
    [2, 5, 31],
    [3, 8, 45],
    [4, 8, 52],
    [5, 13, 79],
    [6, 15, 85],
    [7, 17, 115],
    [8, 19, 119],
    [9, 21, 135],
    # [10, 24, 145],
]
# 2. 进行基本的处理（略）
names = ['id', 'flow', 'sales']
df = pd.DataFrame(data=data, columns=names)

# 3. 特征工程（略）

# 4. 机器学习
# 实例化 API
estimator = LinearRegression()
# 使用 fit 方法进行训练
estimator.fit(df.flow.values.reshape(-1, 1), df.sales)

# 查看系数
print('系数为：', estimator.coef_)

print('预测结果为：', estimator.predict([[24]]))

# 5. 模型评估

二元回归案例

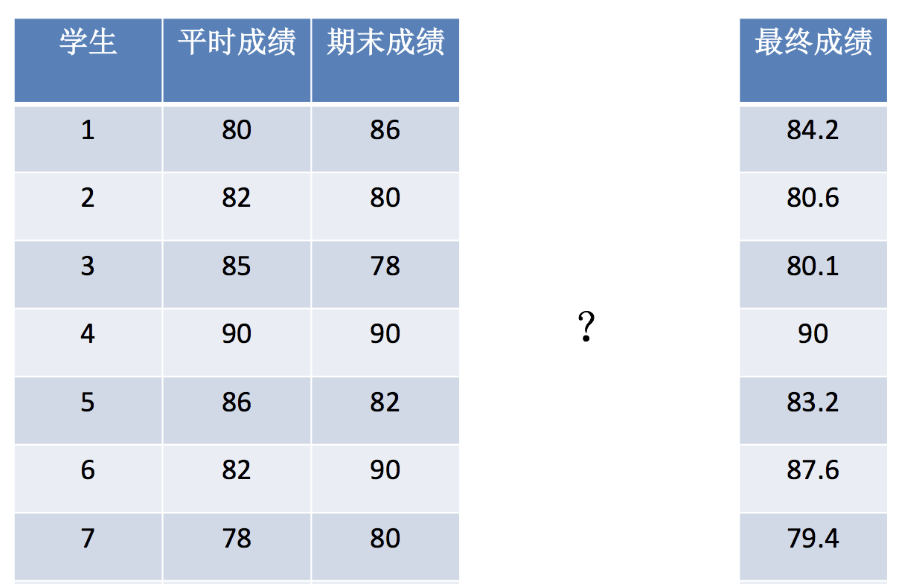
步骤分析

1. 获取数据集
2. 数据基本处理（该案例中省略）
3. 特征工程（该案例中省略）
4. 机器学习
5. 模型评估（该案例中省略）

代码过程

导入模块

from sklearn.linear_model import LinearRegression

构造数据集

x = [[80, 86],
     [82, 80],
     [85, 78],
     [90, 90],
     [86, 82],
     [82, 90],
     [78, 80],
     [92, 94]]
y = [84.2, 80.6, 80.1, 90, 83.2, 87.6, 79.4, 93.4]

机器学习-- 模型训练

# 实例化 API
estimator = LinearRegression()
# 使用 fit 方法进行训练
estimator.fit(x, y)

estimator.coef_

estimator.predict([[100, 80]])

二元线性方程推导

让我们用一个简单的例子来引出二元线性回归模型。为了更形象地描述，假设以下是一个贷款额度模型，根据工资与年龄可以求出一个人贷款的额度。

工资	年龄	额度
4000	25	20000
8000	30	70000
5000	28	35000
7500	33	50000
12000	40	85000

数据：工资和年龄（2 个特征）

目标：预测银行会贷款给我多少钱（标签）

考虑：工资和年龄都会影响最终银行贷款的结果那么它们各自有多大的影响呢？（参数）

X1,X2 就是我们的两个特征（年龄，工资）Y 是银行最终会借多少钱

找到最合适的一条线（想象一个高维）来最好的拟合我们的数据点

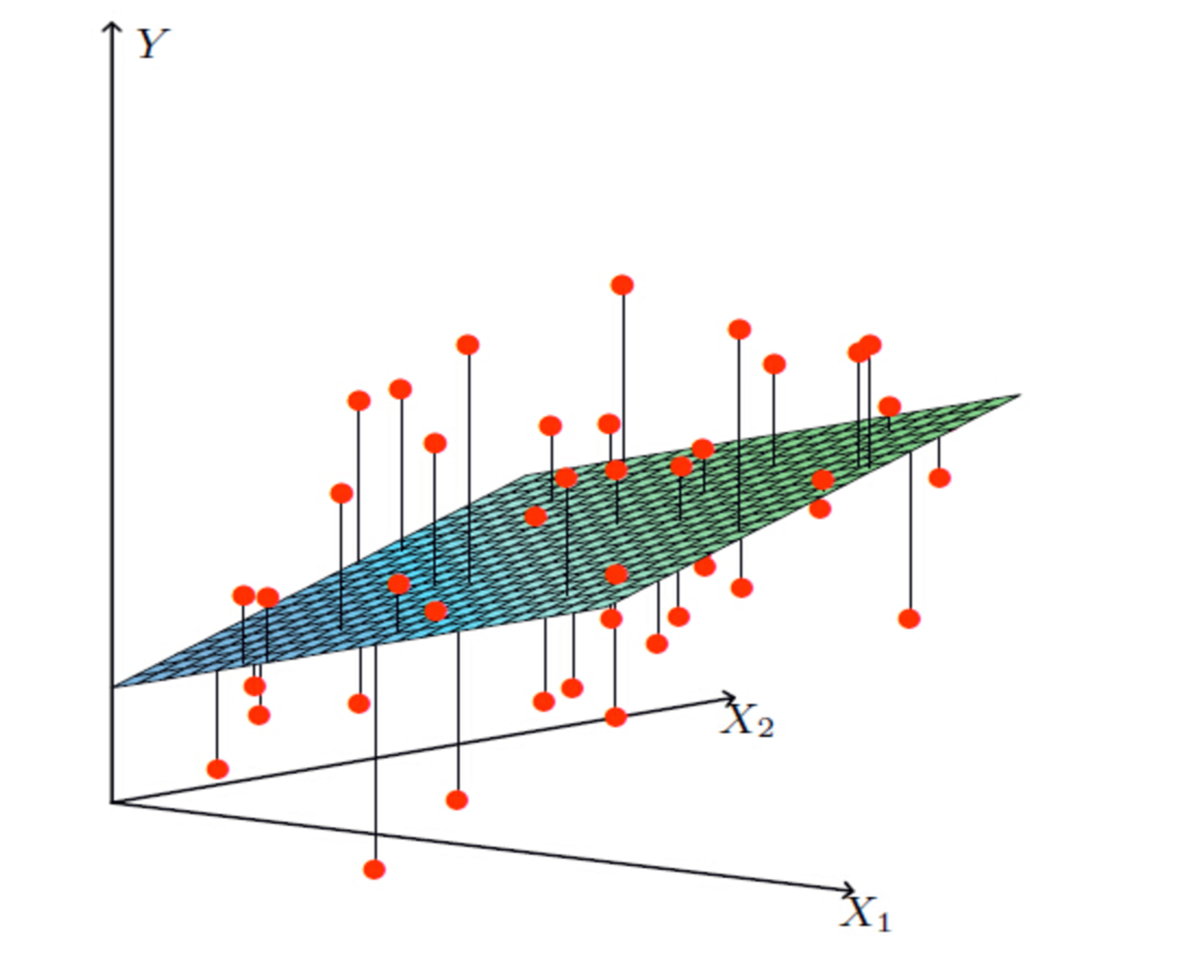
假设 ${\theta }_1$ 是年龄的参数，${\theta }_2$ 是工资参数

拟合的平面：$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2$ （${\theta }_0$ 是偏置项）

整合：

$$h_{\theta }(x)=\sum _{i=0}^n{\theta }_i{x}_i={\theta }^{T}x$$

误差

真实值和预测值之间肯定是要存在差异的（用 $\epsilon$ 来表示该误差）

对于每个样本：

$$y_i={\theta }^T{x}_i+{\epsilon }_i$$

误差 ${\epsilon }_i$ 是独立并且具有相同的分布，并且服从均值为 0 方差为 ${\theta }^2$ 的高斯分布

独立：张三和李四一起来贷款，他俩没关系

同分布：他俩都来得是我们假定的这家银行

高斯分布：银行可能会多给，也可能会少给，但是绝大多数情况下这个浮动不会太大，极小情况下浮动会比较大，符合正常情况

预测值与误差：$y_i={\theta }^T{x}_i+{\epsilon }_i$

由于误差服从高斯分布：

$$p({\epsilon }_i)=\frac{1}{\sqrt{2\pi }\sigma }exp(-\frac{({\epsilon }_i{)}^2}{s{\sigma }^2})$$

将上述二式进行整合

$$p(y_i|x_i;\theta )=\frac{1}{\sqrt{2\pi }\sigma }exp(-\frac{(y_i-{\theta }^T{x}_i{)}^2}{s{\sigma }^2})$$

似然函数：

$$L(\theta )=\prod _{i=1}^{m}p(y_i|x_i;\theta )=\prod _{i=1}^m\frac{1}{\sqrt{2\pi }\sigma }exp(-\frac{(y_i-{\theta }^T{x}_i{)}^2}{s{\sigma }^2})$$

解释：什么样的参数跟我们的数据组合后恰好是真实值

对数似然：

$$logL(\theta )=log\prod _{i=1}^m\frac{1}{\sqrt{2\pi }\sigma }exp(-\frac{(y_i-{\theta }^T{x}_i{)}^2}{s{\sigma }^2})$$

解释：乘法难解，加法就容易了，对数里面乘法可以转换成加法

展开化简：

$$\begin{gathered} \sum _{i=1}^{m}log\frac{1}{\sqrt{2\pi }\sigma }exp(-\frac{(y_i-{\theta }^T{x}_i{)}^2}{s{\sigma }^2}) \\ =mlog\frac{1}{\sqrt{2\pi }\sigma }-\frac{1}{{\sigma }^2}\cdot \frac{1}{2}\sum _{i=1}^m(y_i-{\theta }^T{x}_i{)}^2 \end{gathered}$$

目标：让似然函数（对数变换后也一样）越大越好

使用最小二乘法

$$J(\theta )=\frac{1}{2}\sum _{i=1}^m(y_i-{\theta }^T{x}_i{)}^2$$

化简函数

目标函数：

$$J(\theta )=\frac{1}{2}\sum _{i=1}^m(h_{\theta }(x)-y_i{)}^2=\frac{1}{2}(X\theta -y{)}^T(X\theta -y)$$

求偏导：

$$\begin{array}{rl}{▽}_{\theta }J(\theta )& ={▽}_{\theta }⟮\frac{1}{2}(X\theta -y{)}^T(X\theta -y)⟯\\ & ={▽}_{\theta }⟮\frac{1}{2}(X^T{\theta }^T-y^T)(X\theta -y)⟯\\ & ={▽}_{\theta }⟮\frac{1}{2}({\theta }^T{X}^{T}X\theta -{\theta }^T{X}^{T}y-y^{T}X\theta +y^{T}y)⟯\\ & =\frac{1}{2}⟮2X^{T}X\theta -X^{T}y-(y^{T}X{)}^T\\ & =X^{T}X\theta -X^{T}y\end{array}$$

令偏导数等于 0：

$$\theta =(X^{T}X{)}^{-1}{X}^{T}y$$